Уравнение Клаузиуса-Клапейрона

Рассмотрим двухфазную однокомпонентную систему. При равновесии в соответствии с теоремой равновесия Гиббса:

.

Так как состав фаз постоянен, то химический потенциал компонента зависит только от внешних параметров р и Т:

.

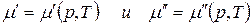Продифференцировав, получим

.

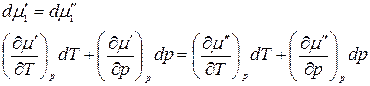Так как химический потенциал чистого компонента – есть парциальная мольная энергия Гиббса (), то

,

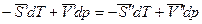где - мольная энтропия компонента в первой и второй фазах соответственно;

- мольный объем компонента в первой и второй фазах соответственно.

Преобразуем:

.

Разность - есть изменение мольной энтропии при переходе вещества из фазы «′» в фазу «″», то есть это энтропия фазового превращения. Тогда

Изменение энтропии при фазовом превращении

,

где – мольная теплота фазового перехода;

Т_ф.п. – температура фазового перехода,

следовательно,

. (2.6)

Полученное уравнение (2.6) – уравнение состояния однокомпонентной двухфазной системы Клаузиуса-Клапейрона.

Применим полученное уравнение к различным процессам.

В процессе плавления производная dp/dT показывает, на какую величину нужно изменить давление, чтобы изменить температуру плавления вещества на 1 градус. Для большинства веществ плотность ρ _т > ρ _ж, тогда и . Следовательно, с повышением давления температура плавления будет увеличиваться. Если ρ _т < ρ _ж, например, для воды (глицерина или висмута), то и и с повышением давления температура плавления будет снижаться.

Для процесса возгонки твердого вещества или испарения жидкости можно допустить, что . Если паровую фазу можно считать идеальной, то в соответствии с уравнением Менделеева-Клапейрона

,

тогда уравнение (2.6) запишется:

.

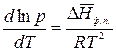Разделив переменные и проинтегрировав в определенных пределах в узком интервале температур, считая постоянной величиной, получим

, (2.7)

где – среднее значение мольной теплоты фазового перехода в интервале температур от Т ₁ до Т ₂.

На основе полученного уравнения (2.7) можно рассчитать:

1) температуру кипения вещества Т₂ под давлением р₂, если известна температура кипения Т₁ этого вещества под давлением р₁ и величина средней мольной теплоты испарения;

2) давление насыщенного пара индивидуального вещества р₂ при температуре Т₂, если известно давление насыщенного пара р₁ при температуре Т₁ и средняя мольная теплота испарения;

3) среднюю мольную теплоту испарения или возгонки вещества, если известны значения давления насыщенного пара вещества при двух температурах.