Спонтанное и вынужденное излучение света. Коэффициенты Эйнштейна.

Мы активно используем термины «лазер», «лазерное излучение» и связанные с ними понятия. Однако особенности работы лазеров и природа лазерного излучения не обсуждались. Вместе с тем в этой области открыты и изучаются фундаментальные особенности электромагнитного поля, нашедшие широчайшее применение в физике, информатике, химии, биологии, медицине, связи. Изучение этих особенностей надо начать с 1905 года, когда Эйнштейн ввел понятие фотона.

В фотоэффекте связанный в металле электрон получал энергию ЭМП в виде энергии дискретного фотона и освобождался, вылетая из металла. Аналогичные процессы происходят в атомах. Если на атом падает ЭМВ, то атом может получить энергию резонансного фотона и перейти в возбужденное состояние (поглощение света). Напротив, возбужденный атом, взаимодействуя с ЭМП, может испустить фотон, перейдя в основное состояние. Квантовомеханическое описание этих процессов проводят в двух приближениях: чисто квантовом, когда и поле, и атом рассматриваются как квантовые объекты, и полуклассическом, когда атом считается квантовым, а поле – заданным и классическим. Второй подход проще (исторически первым изучался именно он) и мы начнем обсуждение с этого случая.

При полуклассическом описании поглощения и испускания света рассматривают уравнение Шредингера со сложным гамильтонианом. Он включает оператор энергии невозмущенной системы , который определяет собственные функции и собственные значения энергии электронов в данном атоме (мы помним, что для этого надо решить весьма сложную квантовомеханическую задачу) и оператор энергии возмущения

, (б.3.1)

т.е. уравнение

. (б.3.2)

Длина волны видимого света намного превышает размеры атома, поэтому неоднородность электрического поля в пространстве обычно не учитывается, а электрическая составляющая световой волны берется в определении (1) в заданном приближении, с определенной амплитудой и частотой,

. (б.3.3)

Применение к задаче (1) - (3) теории возмущений позволяет найти исправленные волновые функции, а их знание дает возможность определить вероятности поглощения или испускания света. Конкретный вид этих вероятностей известен для разных случаев, универсальной формулы нет, поэтому останавливаться на деталях соответствующих формул мы не будем. Заметим, что и в вероятность поглощения, и в вероятность излучения входит квадрат амплитуды поля . Это – ключевой момент: то, что поглощение пропорционально (или интенсивности света, или, в модели Эйнштейна, числу фотонов), достаточно очевидно, однако то, что вероятность испускание света пропорциональна имеющейся интенсивности – неожиданность. Полученный результат имеет существенно квантовый характер, хотя отчасти случаен. Его строгое объяснение возможно только при последовательном квантовом описании излучения.

В приближении заданного поля получается, что чем сильнее поле, в котором находится возбужденный атом, тем вероятнее испускание атомом фотона, причем именно той частоты, как у внешнего поля. По этой причине испускание света такого типа называется индуцированным или вынужденным. Наличие вынужденного излучения определяет возможность создания и работы лазера.

В старом, имеющем сейчас только историческое значение, описании процессов поглощения используют понятия коэффициентов Эйнштейна. Так например, для описания поглощения вводят коэффициент Эйнштейна , который представляет собой сумму вероятностей поглощения данной частоты света , удовлетворяющей правилам отбора Бора

. (б.3.4)

Коэффициент учитывает, что у поглощающей системы может быть несколько «подходящих» переходов типа (4).

Аналогичным образом для испускания света определялся коэффициент Эйнштейна . Оба коэффициента связаны простым соотношением

, (б.3.5)

где и – статистические веса состояни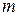й и , то есть числа различных квантовых состояний с энергиями и .

Первоначально роль коэффициентов Эйнштейна состояла в том, чтобы обеспечить баланс поглощенной и испущенной энергии в условиях статистического равновесия теплового излучения. При этом Эйнштейн выделил два канала излучения – вынужденное, с коэффициентом, равным коэффициенту поглощения , и спонтанное, определявшееся различием коэффициентов и . Если, как в квазиклассической теории вынужденное излучение пропорционально интенсивности падающей волны, то спонтанное излучение возникает и без наличия падающей волны, самопроизвольно.

Важнейшей особенностью вынужденного излучения является его когерентность. Это свойство состоит в том, что вынужденно испущенные фотоны обладают в точности теми же параметрами, что и фотоны, стимулирующие излучение. У них одинаковые частоты, одинаковые волновые векторы или направления распространения, одинаковые фазы (понятие фазы фотона сложнее, чем в классической области). При описании в приближении заданного поля это свойство возникает несколько искусственно и его природа не очень ясна. При квантовом описании поля когерентность фотонов есть следствие свойств операторов бозе-частиц (см. ниже), и это свойство появляется автоматически при последовательном квантовом описании процессов излучения.

Объяснить природу спонтанного излучения удалось значительно позже – после развития методов описания квантовых систем, получивших название вторичное квантование. Если обычное квантование это представлений в дискретном виде физических (наблюдаемых) величин, то вторичное квантование – замена амплитуд волновых функций операторными величинами, связанными с числом частиц, находящихся в данном квантовом состоянии. В частности, число фотонов данной частоты заменялось оператором таких фотонов. При этом было установлено, что все гармонические осцилляторы (в том числе и гармонические колебания монохроматического ЭМП) являются бозонами. Мы изучали бозоны и знаем, что их энергия дается выражением

, (б.3.6)

где суммирование проводится по всем типам гармонических осцилляторов, – число осцилляторов данного типа, а слагаемые дают нулевую энергию данного типа колебаний (которая существует при отсутствии колебаний). В гамильтониане, описывающем взаимодействие квантовой система «атом» с квантовой системой «электромагнитное поле» имеется слагаемое, соответствующее невзаимодействующему полю. Это слагаемое имеет вид (6), но с тем отличием, что число фотонов-осцилляторов заменено оператором числа частиц в i-м состоянии, величиной .

Таким образом, бозонный характер фотонов и наличие у них энергии нулевых колебаний означает, что фотоны могут появляться (рождаться) при переходе возбужденного атома на более низкий уровень энергии, что и является корректным изображением спонтанного излучения.

Спонтанный переход, связанный с воздействием поля нулевых колебаний, – важнейшее свойство всех бозонных систем. Существует безумная гипотеза о том, что мозг человека (набор нейронов) обладает бозонными свойствами и способен совершать спонтанные переходы. В рамках этой гипотезы становится понятным, откуда у человека берутся неизвестные ранее научные идеи, художественные образы и простые догадки о том, как решить ту или иную задачу. Более того, известно, что при определенных условиях бозе системы испытывают бозе-конденсацию. Не этим ли определяется единодушие толпы, одинаковые чувства, охватывающие большие массы людей?