Результат выполнения лабораторной работы.

Рис.4. Блок-схема алгоритма E, дополненная примечаниями, которые доказывают правильность работы алгоритма.

Следует A6. Поэтому нам достаточно доказать, что выполнение А6 до шага Е2 влечет за собой выполнение А3 после этого шага. Заметим, что условие d > 0 необходимо в А6 для того, чтобы операция Е2 имела смысл.) Нужно показать также, что из А3 (при условии, что r=0) следует А4, из А3 (при условии, что r≠ 0) следует А5 и т.д. Все это доказывается очень просто.

Если доказать утверждение (7) для каждого блока, то все примечания к стрелкам будут верны в любом случае выполнения алгоритма. Теперь мы можем применить индукцию по числу шагов, т.е. по числу стрелок в блок-схеме. При прохождении первой стрелки (той, которая выходит из блока «Начало») утверждение А1 верно, поскольку мы всегда исходим из предположения, что выходные значения удовлетворяют заданным условиям. Таким образом, утверждение, которое соответствует n-й стрелке, верно.

Исходя из этого общего метода доказательство правильности заданного алгоритма, очевидно, сводиться к нахождению правильных утверждений, соответствующим стрелкам блок-схемы. Как только данное начальное препятствие будет преодолено, останется лишь рутинная работа, связанная с доказательством того, что каждое утверждение влечет за собой утверждение на выходе из блока. В действительности после того как вы придумаете самые трудные из утверждений, найти все остальное уже не составит труда. Скажем, если даны утверждения А1, А4 и А6, уже понятно, какими должны быть утверждения А2, А3 и А5. В нашем

Таблица 1

ТАБЛИЦА БИНОМИАЛЬНЫХ КОЭФФИЦИЕНТОВ (ТРЕУГОЛЬНИК ПАСКАЛЯ)

r

Подсчитать общее число сочетаний из n объектов по k совсем несложно. Соотношение (2) из предыдущего раздела говорит о том, что существует n(n-1) … (n-k+1) способов выбора первых k объектов в перестановке, причем каждое сочетание из k элементов встречается ровно k! раз, так как для любого набора из k объектов существует k! перестановок. Поэтому для числа сочетаний из n элементов по k, которое мы обозначим через , получаем следующую формулу:

(2)

Например,

Это число сочетаний, которое мы нашли в (1).

Величины (читается «число сочетаний из n по k») называются биномиальными коэффициентами и имеют очень широкое применение. Вероятно, это самые важные величины, использующиеся в анализе алгоритмов, поэтому я настоятельно советую читателю познакомиться с ними.

Формулу (2) можно использовать для определения даже в том случае, когда n не является целым числом. Точнее говоря, определим число сочетаний для всех действительных r и всех целых k следующим образом:

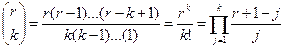, целое k≥ 0; (3)

, целое k< 0.

В частных случаях имеем: , , . (4)

В табл. 1 приведены значения биномиальных коэффициентов для небольших целых величин r и k; биномиальные коэффициенты для 0≤ r≤ 4 следует запомнить.