по высшей математике

ВОПРОСЫ

1. Понятие вектора на плоскости и пространстве. Коллинеарные векторы. Сумма и разность векторов.

2. Умножение вектора на число, угол между векторами, проекция вектора на ось.

3. Скалярное произведение векторов, его свойства. Условие ортогональности векторов.

4. Вектор в координатной форме, радиус – вектор. Разложение вектора по единичным ортам. Длина вектора

5. Операции над векторами, заданными в координатной форме. N – мерное пространство (Rⁿ).

6. Понятие множества. Операции над множествами. Диаграмма Эйлера-Венна.

7. Взаимно–однозначное соответствие между множествами. Счетность, несчетность множества. Ограниченность.

8. Расстояние между точками. Деление отрезка в данном отношении.

9. Уравнение прямой с заданным угловым коэффициентом.

10. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом.

11. Уравнение прямой, проходящей через две заданные точки.

12. Общее уравнение прямой.

13. Уравнение прямой в отрезках.

14. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых.

15. Расстояние от точки до прямой. Неравенства, задаваемые общим уравнением прямой.

16. Каноническое уравнение окружности.

17. Каноническое уравнение эллипса. Эксцентриситет эллипса.

18. Каноническое уравнение гиперболы. Уравнение асимптот.

19. Каноническое уравнение параболы.

20. Матрицы. Основные понятия.

21. Операции над матрицами. Равенство матриц.

22. Умножение матриц.

23. Обратная матрица, ее вычисление.

24. Определители матрицы. Свойства определителей.

25. Минор и алгебраическое дополнение.

26. Вычисление определителей.

27. Системы линейных уравнений.

28. Правило Крамера решения систем линейных уравнений.

29. Метод обратной матрицы.

30. Метод Гаусса. Метод Жордана – Гаусса.

31. Понятие базисных и свободных неизвестных, общего, частного и базисного решения системы.

32. Понятие функции. Способы задания функции.

33. Основные свойства функции (ограниченность, четность, нечетность, периодичность, монотонность).

34. Обратная функция. Сложные и неявно заданные функции.

35. Примеры основных функций и их графики.

36. Понятие последовательности и ее предела. Геометрическая интерпретация предела последовательности.

37. Сходимость последовательност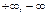и к и к .

38. Понятие предела функции в точке.

39. Понятие бесконечно малой и бесконечно большой функций. Связь между ними.

40. Основные свойства бесконечно малых функций.

41. Основные теоремы о пределах функции.

42. Виды неопределенности и их раскрытие. Первый и второй замечательные пределы.

43. Односторонние пределы функции и их связь с пределом функции в точке.

44. Сравнение бесконечно малых функций.

45. Непрерывность функции в точке и на отрезке.

46. Основные теоремы о непрерывных функциях.

47. Непрерывность слева и справа. Разрывы функции. Типы разрывов.

48. Свойства функций, непрерывных на отрезке.

49. Понятие производной, ее геометрический смысл. Уравнения касательной.

50. Понятие дифференцируемости функции в точке, ее дифференциала.

51. Связь между дифференцируемостью функции и непрерывностью.

52. Основные правила дифференцирования.

53. Производная сложной функции.

54. Обратная функция и ее производная.

55. Производные основных элементарных функций.

56. Производные и дифференциалы высших порядков.

57. Правило Лопиталя раскрытия неопределенности.

58. Теоремы Ролля и Лагранжа.

59. Формула Тейлора и Маклорена.

60. Применение производной для исследования динамики функции. Критерии монотонности функции.

61. Экстремум функции, его нахождение.

62. Выпуклость функции, точки перегиба.

63. Асимптоты функции.

64. Множества в пространстве Rⁿ.

65. Функции двух и более переменных. Понятие предела и непрерывности функции двух переменных в точке.

66. Частные производные и частный дифференциал функции двух переменных.

67. Полный дифференциал функции. Понятие дифференцируемости функции двух переменных, ее дифференциала.

68. Производные высших порядков функции двух переменных. Теорема о смешанной производной.

69. Экстремум функции двух переменных. Необходимое и достаточное условия экстремума функции двух переменных.

70. Производная по направлению. Градиент функции двух переменных.

71. Условный экстремум.

72. Метод наименьших квадратов. Выравнивание по прямой.

73. Выравнивание с помощью кривых (по гиперболе и по параболе).

74. Первообразная. Понятие неопределенного интеграла. Его свойства.

75. Методы интегрирования. Непосредственное интегрирование. Метод замены переменной.

76. Интегрирование по частям в неопределенном интеграле.

77. Понятие правильной и неправильной рациональной дроби. Разложение правильной рациональной дроби на простейшие дроби.

78. Интегрирование некоторых видов иррациональностей.

79. Интегрирование тригонометрических выражений.

80. Задача о нахождении площади криволинейной трапеции.

81. Понятие определенного интеграла.

82. Основные свойства определенного интеграла.

83. Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

84. Формула замены в определенном интеграле. Формула интегрирования по частям в определенном интеграле.

85. Применение определенного интеграла к вычислениям площадей фигур и объемов тел вращения.

86. Несобственный интеграл первого рода и его сходимость.

87. Несобственный интеграл второго рода и его сходимость.

88. Понятие двойного интеграла и его вычисление в случае прямоугольной области.

89. Понятие числового ряда и его суммы. Сходимость ряда.

90. Свойства сходящихся рядов.

91. Понятие остатка ряда. Теорема об остатке.

92. Необходимый признак сходимости ряда.

93. Гармонический ряд и его сходимость.

94. Признаки сравнения положительных рядов.

95. Признак Даламбера сходимости положительных рядов.

96. Радикальный и интегральный признаки Коши.

97. Знакочередующиеся ряды. Признак Лейбница.

98. Условно и абсолютно сходящиеся ряды. Теорема Римана.

99. Понятие функционального и степенного рядов.

100.Теорема Абеля. Область сходимости степенного ряда.

101.Свойство суммы степенного ряда. Теорема о почленном дифференцировании и интегрировании степенных рядов.

102.Разложение функции в степенной ряд. Ряд Тейлора и Маклорена.

103.Понятие о дифференциальном уравнении, его порядке и решении.

104.Задача Коши. Общее и частное решение.

105.Дифференциальные уравнения с разделяющимися переменными.

106.Однородные дифференциальные уравнения.

107.Линейные дифференциальные уравнения первого порядка.

108.Линейные дифференциальные уравнения второго порядка. Теоремы об общем решении линейных однородных и неоднородных уравнений второго порядка.

109.Нахождение общего решения линейного однородного уравнения второго порядка с постоянными коэффициентами.

110.Нахождение частного решения линейного неоднородного уравнения второго порядка с постоянными коэффициентами.