
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть
|
|
Москва
Г.
Цель работы: изучение методов формирования базовых моделей для расчета токов в неоднородных средах и исследование распределения плотности токов в тканях конечности при биоадекватном воздействии.
Теоретическая часть

При проведении расчетов распределения токов в модели конечности принимались следующие допущения:
- все объекты модели имеют осевую симметрию;
- кость расположена по центру конечности;
Расчет проводился в 3 этапа:
1. Оценивалось распределение токов в срединной плоскости протяженного (L> > R) однородного цилиндра, состоящего только из мышечной ткани;
2. Проводился расчет распределения токов в кости, расположенной в бесконечной однородной проводящей среде (мышечная ткань) в поле однородного тока (т.к. результаты расчетов пункта 1 позволяют с точностью до 10-15% принять плотность тока в области кости однородной);
3. Рассматривался сосуд в бесконечной однородной проводящей среде в поле однородного тока (п.1).
Этап 1. Распределение тока в однородной проводящей цилиндрической системе:
 (1)
(1)

j(z) – комплексное, С1 – действительная константа
Общий ток в конечности:
 (2)
(2)
При подстановке (1) в (2) обозначим
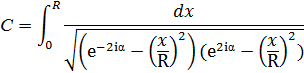

Используя стандартную форму записи неполного эллиптического интеграла 1-го рода, получим


Где 
Отсюда:

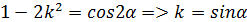
Неполный эллиптический интеграл выражают через полный эллиптический, ограничиваясь 3мя членами разложения, находят выражение для константы С и записывают решение (1) в полярных координатах:

 ,
,




Этап 2. Для нахождения распределения плотности тока в области однородного включения в бесконечной проводящей среде в поле однородного тока используется общее решение уравнения Лапласа (в полярных координатах):


Особенности задачи:
- задача симметрична  => члены с
=> члены с  отсутствуют;
отсутствуют;
- решение должно иметь период 2π;
- примем потенциал в центре кости равным нулю;
Получаем распределение потенциала:

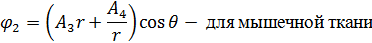

Из граничных условий находим значения коэффициентов A1, A2, A3, A4, A5, A6.
Этап 3. При расчетах этапа 3 в качестве исходного поля плотности тока, окружающего сосуд, используем рассчитанные на этапе 2 значения. Расчет проводится аналогично этапу 2 с значениями проводимости для сосудистой стенки и крови.
С помощью полученных формул можно найти плотность тока в любой точке рассматриваемой модели.