
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
семестр
|
|
Контрольная работа для заочного отделения
семестр
Вопросы
- Матрицы. Операции над матрицами. Определения квадратной, нулевой, ступенчатой матрицы. Приведение матрицы к ступенчатому виду. Обратная матрица. Алгоритм вычисления обратной матрицы.
- Определители второго и третьего порядка. Свойства определителей. Способы нахождения (вычисления) определителей 1-го, 2-го, 3-го и 4-го порядков. Миноры и алгебраические дополнения элементов. Вычисления определителя разложением его по строке, столбцу.
- Системы линейных уравнений. Система двух уравнений первой степени с двумя неизвестными. Однородная система двух уравнений первой степени с тремя неизвестными. Способы нахождения решений СЛУ. (Матричный метод, метод Гаусса, метод Крамера). Теорема Кронекера-Капелли. Ранг матрицы.
- Векторы. Обозначения векторов. Линейные операции над векторами. Линейная зависимость и линейная независимость векторов. Ортонормированный базис. Скалярное, векторное и смешанное произведение векторов, их свойства.
- Аналитическая геометрия на плоскости. Уравнения линии и прямой. Общее уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой на плоскости. Параметрическое уравнение прямой на плоскости.
- Кривые второго порядка. (Эллипс, окружность, гипербола, парабола). Уравнения и графики.
- Плоскость и прямая в пространстве. Уравнение плоскости. Исследование общего уравнения плоскости. Условия параллельности и перпендикулярности плоскостей. Каноническое уравнение прямой в пространстве.
8. Параметрическое задание линии. Примеры линий, заданных параметрически.
9. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Конусы. Эллипсоид. Гиперболоиды. Параболоиды. Геометрические свойства этих поверхностей, исследование их формы методом сечений.
10. Полярные координаты на плоскости. Спираль Архимеда.
11. Цилиндрические и сферические координаты в пространстве. Различные способы задания линий и поверхностей в пространстве.
Рекомендуемая литература
- Н.Ш. Кремер «Высшая математика для экономистов»
- Д.В. Клетеник «Сборник задач по аналитической геометрии»
- И.А.Каплан «Практические занятия по высшей математике» часть 1.
- Б.М. Владимирский «Математика. Общий курс»
- П.Е.Данко, А.Г. Попов «Высшая математика в упражнениях и задачах» часть 1.
Пример оформления титульного листа
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Южно-Уральский государственный университет»
Филиал ГОУ ВПО «ЮУрГУ» в г. Златоусте
Кафедра «Математика и вычислительная техника»
Контрольная работа
По дисциплине: ”математика”
Вариант № 100
Выполнил студент 1 курса
Заочного отделения
Гр…..-166
Иванов И.И.
Проверил………….
Златоуст
2011г.
Введение.
Выполнять контрольную работу следует строго по графику. Каждый студент выполняет контрольную работу под вариантом, номер которого совпадает с его порядковым номером в групповом журнале. Решение задач нужно предоставить в письменном виде на отдельных листах (формата А 4, в скрепленном виде). Сдавать работу можно как в печатном, так и в письменном виде. Выполняя к.р., студент должен переписать условие соответствующей задачи, написать подробное решение, выделив ответ. Там, где это необходимо, дать краткие пояснения по ходу решения.
Задача 1.
Для данного определителя найти миноры и алгебраические дополнения элементов 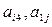 .Где i и j, определяются следующим образом: для четного варианта i=2, j=4, для нечетного i=1, j=3 Вычислить определитель:
.Где i и j, определяются следующим образом: для четного варианта i=2, j=4, для нечетного i=1, j=3 Вычислить определитель:
а) разложив его по элементам j-й строки
б)получив предварительно нули в i-й строке
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
Задача 2.
Проверить совместность системы и в случае совместности решить её:
а)методом Крамера
б)матричным методом
в)методом Гаусса
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
Задача 3.
Решить матричное уравнение
1.  2.
2. 
3.  4.
4. 
5. 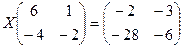 6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15. 
Задача 4.
Выясните, образуют ли векторы  базис. Если образуют, то разложите вектор
базис. Если образуют, то разложите вектор  по этому базису.
по этому базису.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
Задача 5.
Заданы вершины треугольника АВС. Вычислите его площадь и косинус внутреннего угла В.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 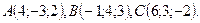
11. 
12. 
13. 
14. 
15. 
Задача 6.
1. Найдите объем параллелепипеда, построенного на векторах  , если
, если 
- Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - Найдите объем параллелепипеда, построенного на векторах

- Найдите объем тетраэдра, построенного на векторах

- Вычислите объем тетраэдра с вершинами в точках

- Найдите объем параллелепипеда, построенного на векторах
 , если
, если 
- Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - Найдите объем параллелепипеда, построенного на векторах

- Найдите объем треугольной пирамиды с вершинами в точках

- При каком значении к точки лежат в одной плоскости

- Найдите объем тетраэдра с вершинами в точках

- При каком значении m векторы
 компланарны?
компланарны? - Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - При каком значении m векторы
 компланарны?
компланарны? - Вычислите объем тетраэдра с вершинами в точках

Задача 7.
В треугольнике АВС составьте уравнения:
1) стороны ВС;
2) высоты, опущенной из вершины А на сторону ВС;
3) медианы, проведенной из вершины С.
1. 
2. 
3. 
4. 
5. 
6. 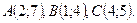
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Задача 8.
Приведите уравнение кривой второго порядка к каноническому виду и постройте её. Укажите координаты вершин, фокусов. Напишите уравнение директрисы и асимптот, если они есть. Вычислите эксцентриситет кривой.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Задача 9.
Напишите каноническое уравнение прямой, проходящей через точку А и перпендикулярной плоскости α.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Задача 10.
Нарисуйте область, ограниченную заданными поверхностями.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 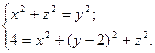
13. 
14. 
15. 
|