Свойства бесконечно малых функций.

1. Алгебраическая сумма конечного числа БМ Ф есть БМФ при .

2. Произведение БМ Ф на ограниченную в некоторой окрестности точки функцию (в т.ч. на постоянную, на другую БМ) есть БМ Ф.

3. Частное от деления БМ Ф на функцию, предел которой отличен от нуля, есть БМ Ф.

Замечание. Свойство 3 не рассматривает предел отношения двух БМ Ф из-за его неопределенности: он может быть равен как конечному числу, так и .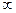

Докажем, например, свойство 1.

Пусть и есть БМ Ф. Докажем, что функция также есть БМ Ф.

По условию для любого , а значит, и для найдутся такие числа и , что :

если , то

(1)

если , то

(2)

Если в качестве 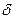взять минимальное из и , т.е. , то для всех х, удовлетворяющих условию будут верны оба неравенства (1) и (2). Складывая их почленно, получим:

.

Используя первое неравенство треугольника, перейдем к более сильному неравенству:

.

Итак, мы нашли , такое, что при всех выполняется неравенство . Это и означает, что функция есть БМ Ф. ▲

Свойства бесконечно больших функций.

1. Произведение ББ Ф на функцию, предел которой отличен от 0, есть ББ Ф.

2. Сумма ББ Ф и ограниченной функции есть ББ Ф.

3. Сумма ББ Ф одного знака есть ББ Ф того же знака.

4. Частное от деления ББ Ф на функцию, имеющую конечный предел, есть ББ Ф.

Сравнение бесконечно малых функций.

Пусть и - БМ Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.

. Тогда если:

1) А – число, не равное 0 или 1, то функции и называются БМ одинакового порядка.

2) А=0, то функция называется БМ более высокого порядка малости, чем и обозначают: (о малое).

Пример:

, - БМ при х→ 0,

3) А= , то функция называется БМ более высокого порядка малости, чем .

4) А =1, то функции и называются эквивалентными БМ , обозначается: ~ .