Пошук власних векторів

Метод послідовності Штурма для характеристичного поліному.

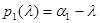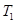Нехай - підматриця Т з перших i рядків та стовпців. Тоді поліном - характеристичний поліном ;

- характеристичний поліном ;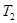

………………………………….

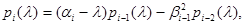i=2, 3, …, n,

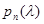- характеристичний поліном матриці Т.

Нехай формально .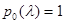

Якщо 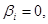то поліном розпадається на добуток двох множників. Розгляньмо випадок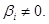

Теорема про чередування нулів. Якщо то.

Доведення Нехай i=1. 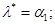ОК.

Нехай при деякому i Тоді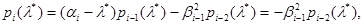

тому Позаяк 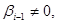то якщ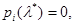о то 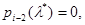ідучи назад до i=1, маємо 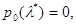але 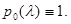Маємо протиріччя.

Dixi.

Використання теореми. Уважний аналіз послідовності 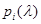виявляє, що вона є послідовністю Штурма.

Кількість змін знаку у послідовності Штурма є функцією монотонно спадною; треба знайти 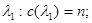знайти 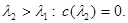Тоді - межі спектру.

Пошук власних векторів

Якщо -власний вектор Т. Тоді -власний вектор А.

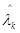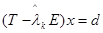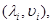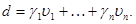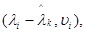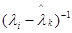Нехай -наближене значення . Тоді Нехай . i=1, …, n – спектр матриці Т. Тоді Матриця має спектр i=1, …, n. Матриця має власні числа , вектори , тому .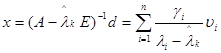

Якщо 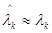, то член 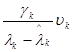домінуватиме і х можна вважати наближенням до . Вектор d може бути довільним, з точністю ”до множини міри нуль” (з нульовою ймовірністю). У крайньому разі, якщо х – погане наближення, можна знайшовши , взяти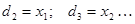