
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Інтерполяційний многочлен Лагранжа та його залишковий член.
|
|
Постановка задачі.
Найпростіша задача інтерполювання виглядає так. На відрізку [a, b] у точках х0, х1, …хn, де a≤ х0< x1< …< xn≤ b, задані значення деякої функції f(x):
f(x0)=y0, f(x1)=y1, …, f(yn)=yn.
Треба побудувати функцію F(x), яка належить до визначеного класу і в точках х0, x1, …, xn набуває таких значень, що й f(x), тобто F(x0)=y0, F(x1)=y1, …, F(xn)=yn.
Точки х0, x1, …, xn прийнято називати вузлами інтерполювання, а функцію F(x) – інтерполяційною функцією.
Інтерполяційний многочлен Лагранжа та його залишковий член.
Нехай f(x) є R і х0, x1, …, xn (хі є [a, b], при i ≠ j) – вузли інтерполювання. Побудуємо інтерполяційний многочлен φ (x), де за систему лінійно незалежних функцій {φ (x)} виберемо систему:
 φ 0(x)=1, φ 1(x)=х, φ 2(x)=х2, φ n(х)=хn. Запишемо φ (х) у вигляді φ (х)=
φ 0(x)=1, φ 1(x)=х, φ 2(x)=х2, φ n(х)=хn. Запишемо φ (х) у вигляді φ (х)=  f(xi)Фni(x), де Фni(x) – у цьому випадку многочлени степеня n, які задовольняють умову: 1, якщо і=j,
f(xi)Фni(x), де Фni(x) – у цьому випадку многочлени степеня n, які задовольняють умову: 1, якщо і=j,
Фni(x) =
0, якщо і≠ j.
Ці многочлени можна відшукати, розв’язавши систему рівнянь  α іφ і(xj)=f(xj) (j=0, 1, …, n).
α іφ і(xj)=f(xj) (j=0, 1, …, n).
Однак їх можна визначити і не розв’язуючи системи рівнянь. Позаяк Фni(x) є многочленом степеня n, котрий набуває значення нуль у точках х0, x1, …, хі–1, хі+1, …, xn і дорівнює одиниці в точці хі, то
 . З умови Фni(xі)=1 одержуємо, що
. З умови Фni(xі)=1 одержуємо, що  . Тому
. Тому
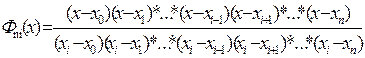 . Отже, шуканий інтерполяційний многочлен, який позначимо через Ln(x), має такий вигляд:
. Отже, шуканий інтерполяційний многочлен, який позначимо через Ln(x), має такий вигляд:
 і називається інтерполяційним многочленом Лагранжа, а многочлени Фni(xі) – фундаментальними многочленами.
і називається інтерполяційним многочленом Лагранжа, а многочлени Фni(xі) – фундаментальними многочленами.
Многочлен Лагранжа збігається з функцією f(x) у вузлах інтерполювання. В інших точках [a, b] маємо наближену рівність f(x)=Ln(x). Різниця Rn+1(x)=f(x)–Ln(x) називається залишковим членом інтерполяційного многочлена Лагранжа.
Для обчислення функції f(x) в точці 2, 7 напишемо програму (додаток 1 мал.2).
|