Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
|
Дробные числа
Наряду с необходимостью считать предметы у людей с древних времён появиласьпотребность измерять длину, площадь. Объём, время и другие величины.Приходится учитывать и части употребляемой меры. Так возникли дроби.В истории развития дробного числа мы встречаем дроби трёх видов: 1) доли или единичные дроби, у которых числитель единица, знаменателем жеможет быть любое целое число; 2) дроби систематические, у которых числителями могут быть любые числа, знаменателями же – только числа некоторого частного вида, например степенидесяти или шестидесяти; 3) дроби общего вида, у которых числители и знаменатели могут быть любымичислами.Изобретение этих трёх различных видов дробей представляло для человечестваразные степени трудности, поэтому разные виды дробей появлялись в разныеэпохи.Знакомство человека с дробными числами началось с единичных дробей с малымизнаменателями.Понятия «половина», «треть», «четверть», «осьмушка» употребляются частолюдьми, которые арифметике дробных чисел никогда не обучались. Эти простейшиедроби изобрёл каждый народ самостоятельно в ходе своего развития. Единичные дроби. Древние египтяне, несмотря на то, что в течениенескольких тысячелетий своей истории развили высокую культуру, оставили послесебя прекрасные памятники искусства, владели многими отраслями техники, однако в арифметике дробных чисел не пошли далее изобретения единичных дробей(и дроби
). Еслизадача приводила к ответу, который мы выражаем дробным числом, египтяне егопредставляли в виде суммы единичных дробей или долей. Если, например, ответ понашему был 
, египтянепредставляли его в виде суммы 
+ 
+ 
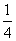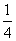
и писали без знаков сложения: . Без знака сложения обходились и многие позднейшие народы, понимая писаниедробей рядом, как сложение. Этот египетский способ письма частично сохранился иу нас. Мы пишем смешанные числа, ставя рядом, без какого-либо соединяющегознака, число целых единиц и дробей, и понимаем запись, как сумму: пишем 
вместо 
.Может показаться, что египетский способ пользования одними лишь единичнымидробями делал решение задач сложным. Не всегда это так. Например, египетскийавтор решает задачу: нужно разделить 7 хлебов поровну между восемью лицами. Мысказали бы, что каждый получает хлеба.Для египтянина не было числа , но он знал, что от деления 7 на 8 получается + + 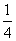. Этот факт подсказывает ему, что для делёжа семи хлебов между восемью лицаминужно иметь 8 половинок, 8 четвертей и 8 осьмушек. Он режет 4 хлеба пополам, 2хлеба – на четвертинки и 1 хлеб – на осьмушки и распределяет доли междуполучающими. Для делёжа пришлось сделать всего 4+6+7=17 разрезов.Кладовщик, работающий в наши дни, которому предстоит такая же задача деленияхлебов, сообразив, что каждому получателю надо дать семь восьмушек, бытьможет, сочтет нужным разрезать все 7 хлебов предварительно на восьмушки, длячего ему требуется сделать 7х7=49 размеров. Как видим, в этой задачеегипетский способ решения является более практичным.Решение задач практической жизни при помощи одних лишь долей (египетскийспособ) имело место почти у всех европейских народов, начиная с греков. Систематические дроби. Одновременно с единичными дробями появились исистематические дроби. Самый ранний по времени вид таких дробей естьшестидесятеричные дроби, употреблявшиеся в древнем Вавилоне. В этих дробяхзнаменателем служат числа 60; 602 = 3600, 603 = 261 000, 604, 605 и т.д., и они сходны с нашими десятеричнымидробями.Шестидесятеричными дробями пользовались все культурные народы до XVII века, особенно в научных работах, поэтому они и назывались физическими илиастрономическими дробями, а дроби общего вида, в отличие от них – обыкновеннымиили народными. Следы пользования этими дробями остались у нас до сих пор: минута есть 1/60, секунда 1/602 = 1/3600, терция 1/603 =1/216 000 часть числа. Десятичные дроби. Десятичные дроби представляют также вид систематическихдробей.К десятичным дробям математики пришли в разные времена в Азии и в Европе.Зарождение и развитие десятичных дробей в некоторых странах Азии было тесносвязано с метрологией (учением о мерах). Уже во II в. до н.э. тамсуществовала десятичная система мер длины.Примерно в III в н.э. десятичный счет распространился на меры массы и объёма.Тогда и было создано понятие о десятичной дроби, сохранившей метрологическуюформу.Вот, например, какие меры массы существовали в Китае в X веке: 1 лан = 10 цянь =102 фэнь = 103 ли = 104 хао = 105сы = 106 хо.Если вначале десятичные дроби выступали в качестве метрологических, конкретных дробей, десятых, сотых и т.д. частей более крупных мер, то позже они по существу стали все более приобретать характер отвлеченныхдесятичных дробей.Целую часть от дробной стали отделять особым иероглифом «дянь» (точка).Однако в Китае, как и в древние, так и в средние века десятичные дроби неимели полной самостоятельности, оставаясь в той или иной мере связанными сметрологией.Более полную и систематическую трактовку получают десятичные дроби в трудахсреднеазиатского ученного ал-Каши в 20-х годах XV в. Независимо от него, в80-х годах XVI в. десятичные дроби были «открыты» заново в Европенидерландским математиком Симоном Стевином.В Средней Азии и в Европе ученые пришли к десятичным дробям по аналогии сшестидесятеричными и разработали теорию десятичных дробей.В середине века ученые пользовались десятичной нумерацией для вычислений с целыми числами, а шестидесятеричной – для вычислений с дробями вастрономии и других отраслях науки. Это породило трудности, связанные спереходом от одного основания к другому.Нелегко усваивались обыкновенные дроби. Вообще считались самым труднымразделом арифметики. Поныне у немцев осталась поговорка «Попал в дроби», т.е.попал в трудное положение.Идея шестидесятеричных дробей, идея одинакового систематического подразделенияцелого на одни и те же доли, с одной стороны, привели к мысли о десятичных дробях.Среднеазиатский город Самарканд был в XV в. большим культурным центром. Там взнаменитой обсерватории, созданной видным астрономом Улугбеком, внукомТамерлана, работал в 20-х годах XV в. крупный ученый того времени – ДжемшидГиясэддин ал-Каши. Это он впервые изложил учение о десятичных дробях.В своей книге «Ключ арифметики», написанной в 1427 г., ал-Каши пишет: «Астрономы применяют дроби, последовательными знаменателями которых являются60 и его последовательные степени. По аналогии мы ввели дроби, в которыхпоследовательными знаменателями являются 10 и его последовательные степени.».Ал-Каши называет сотые доли «десятичными секундами», тысячные – «десятичнымитерциями» и т.д. Термины эти заимствованы из шестидесятеричной нумерации.Вводя десятичные дроби, ал-Каши поставил себе задачу создать простую иудобную систему дробей, основанную на десятичной нумерации и имеющую те жепреимущества, которые имели для вавилонян шестидесятеричные дроби.Ал-Каши излагает правила и приводит примеры действий с десятичными дробями. Оновводит специфическую для десятичных дробей запись: целая и дробная частьпишутся в одной строке. Для отделения первой части от дробной он не применяетзапятую, а пишет целую часть чернымичернилами, дробную же – красными или отделяет целую часть от дробнойвертикальной чертой.Открытие десятичных дробей ал-Каши стало известно в Европе лишь спустя 300 летпосле того, как эти дроби были в конце XVI в. заново открыты С. Стевины.Фламандский инженер и ученый Симон Стевин (1548-1620), около 150 лет послеал-Каши, изложил учение о десятичных дробях в Европе. В 1585 г. он написалнебольшую книгу под названием «Десятая».Эта книга состояла всего лишь из 7 страниц, однако содержала всю теориюдесятичных дробей.Запись десятинных дробей у Стевина была отличной от нашей. Вот, например, какон записывал число 35, 912: 35 0 9 1 1 2 2 3 илиИтак, вместо запятой нуль в кружке. В других кружках или над цифрамиуказывается десятичный разряд: 1 – десятые, 2 – сотые и т.д.Стевик указывал на большое практическое значение десятичных дробей инастойчиво пропагандировал их. Он был первым ученым, потребовавшим введениядесятичной системы мер и весов. Эта мечта ученого была осуществлена лишьспустя свыше 200 лет, когда была создана метрическая система мер. Дробь общего вида. Дроби общего вида 
, в которых и m, и n могут быть произвольными целыми числами, появляются уже внекоторых сочинениях Архимеда. Простейшие из таких дробей (2/3, 3/4) постепенновходят в употребление в житейской практике. Индусы уже в первые века нашеголетосчисления установили современные правила действий над обыкновеннымидробями. Эти правила через руководство среднеазиатских математиков – ал-Хорезмии других – вошли в европейские учебники арифметики. Это случилось ранеераспространения десятичных дробей.В «Арифметики» (1703) первого русского педагога-математика ЛеонтияФилипповича Магницкого (1669-1739) обыкновенные дроби излагаются подробно, десятичные же дроби – в специальной главе, как некоторый новый вид счисления, не имевшего при тогдашней системе мер большого практического значения. Толькос введением метрической (десятичной) системы мер десятыми дроби занялиподобающее место в нашем обиходе. Данная страница нарушает авторские права?