Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экспериментальное изучение свойств ферромагнетиков.
|
|
Большой вклад в экспериментальное изучение свойств ферромагнетиков внес А. Г. Столетов. Предложенный им экспериментальный метод заключался в измерении магнитного потока Фm в ферромагнитных кольцах при помощи баллистического гальванометра.
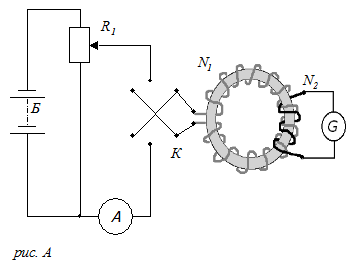Тороид, первичная обмотка которого состояла из N1 витков, имел сердечник из исследуемого материала (например, отожженного железа). Вторичная обмотка из N2 витков была замкнута на баллистический гальванометр G (рис. А). Обмотка N1 включалась в цепь аккумуляторной батареи Б. Напряжение, приложенное к этой обмотке, а, следовательно, и силу тока I1 в ней можно было изменять с помощью потенциометра R1. Направление тока изменялось посредством коммутатора К.
При изменении направления тока в обмотке N1 на противоположное, в цепи обмотке N2 возникал кратковременный индукционный ток и через баллистический гальванометр проходил электрический заряд q, который равен отношению взятого с обратным знаком изменения потокосцепления вторичной обмотки к электрическому сопротивлению R в цепи гальванометра:
 |
Если сердечник тонкий, а площадь поперечного сечения равна S, то магнитная индукция поля в сердечнике
Напряженность магнитного поля в сердечнике вычисляется по следующей формуле
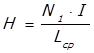
где Lср – средняя линия сердечника.
 |
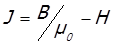Зная B и H можно найти намагниченность
Рассмотрим еще один способ экспериментального изучения свойств ферромагнетиков (на наш взгляд один из наиболее наглядных).
Данный метод аналогичен предыдущему, но отличие состоит в том, что в место гальванометра применяется электронный осциллограф. При помощи осциллографа Осц (см. ниже схему) мы получаем наглядное подтверждение явления магнитного гистерезиса, наблюдая петлю на экране прибора.
Рассмотрим устройство экспериментальной установки.
 |
Напряжение снимаемое с потенциометра Rр пропорционально намагничивающему току I, а следовательно, напряженности поля в экспериментальном образце Эо. Далее, сигнал, снимаемый с реостата Rр, подается на вход (Х), т.е. на пластины горизонтального отклонения осциллографа.
С входа интегрирующей цепочки (пунктирный прямоугольник на схеме) снимается напряжение Uc, которое пропорционально скорости изменения магнитной индукции, т.е. подается на вход (Y) осциллографа, пластины вертикального отклонения.
Рассмотрим работу интегрирующей цепочки.
| Способ I, расчета магнитной индукции. |
 |
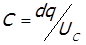Известно, что емкость конденсатора можно вычислить по следующей формуле
 |
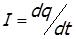где dq – заряд, значение которого можно определить зная ток I
 |
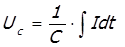Таким образом, напряжение на конденсаторе определяется по следующей формулой
При достаточно больших величинах сопротивления R 
(по сравнению с сопротивлением остальной части цепи) напряжение на емкости Uc значительно меньше напряжения на клеммах AD (Uc < < E), поэтому
Пренебрегая незначительным падением напряжения во вторичной обмотке экспериментального образца Эо, принимаем, что напряжение E на клеммах AD равно электродвижущей силе (ЭДС), индицируемой во вторичной обмотке, которая равна - dФ/dt.
 |
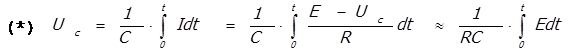Магнитный поток dФ пропорционален изменению магнитной индукции dВ в контуре площадью S, т.е. dФ=dВ · S.
 |
Отсюда можно сделать вывод, что напряжение Е на клеммах AD равно
т.е. пропорционально приращению магнитной индукции dВ.
 |
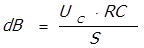Подставляя значение напряжения Е в формулу (*), и преобразовав ее получаем
где S — площадь контура, который охватывает один виток обмотки, т.е. площадь поперечного сечения магнитопровода Эо (экспериментального образца);
Uc – значение напряжения снимаемое с конденсатора С, которое определяется по показаниям осциллографа (вертикально отклоняющий сигнал).
 | |||
 | |||
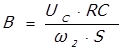Данная формула справедлива при условии, что мы рассматриваем один виток обмотки. Если у нас количество витков обмотки равно ω 2, то окончательно формула будет выглядеть следующем образом
Таким образом, с выхода интегрирующей цепочки мы снимаем зависимость магнитной индукции В от напряжения Uc.
Теперь рассмотрим как зависит напряженность магнитного поля H от напряжения снимаемого с реостата Rр.
Для этого рассмотрим сигнал, поступающий на вход (Х) осциллографа. Ранее мы сказали, что напряжение, снимаемое с потенциометра Rр, пропорционально напряженности поля в экспериментальном образце Эо. Покажем это.
 |
Известно, что циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура равна результирующему макротоку, сквозь поверхность натянутую на этот контур:
В нашем случае значение макротока Iмакро определяется следующем образом:
с реостата Rр мы снимаем напряжение URр, которое подается на горизонтально отклоняющие пластины осциллографа. Зная значение сопротивления на реостате Rр и значение напряжения URр (которое фиксируется при помощи осциллографа) мы получаем, что значение Iмакро = URр/Rр.
 | |||
 | |||
Т.к. контур Эо у нас постоянен, то окончательно формула примет вид
где LСрТр – средняя магнитная линия магнитопровода.
| Способ II, расчета магнитной индукции. |
Рассмотренный ранее способ расчета магнитной индукции груб, т.к. в процессе расчета, формула (*), вносится некоторая не точность в вычисления (падение напряжения во вторичной обмотке). Существует более точный способ, который рассматривает переходные процессы в RC — цепи (интегрирующей цепи).
Рассмотрим данный способ.
Для большей понятности построим схему RC– цепи.
 |
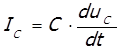Напряжение U0 (входное напряжение или ЭДС вторичной обмотки) определяется как сумма (uR + uc), при этом токи в резисторе и на конденсаторе равны IR=IC. Исходя из того, что емкость С есть отношение заряда q к падению напряжения на конденсаторе UС, а ток в цепи есть скорость изменения заряда, можно записать, что
 |
Таким образом, следует, что ток IR в резисторе можно вычислить по следующей формуле:
Отсюда, входное напряжение U0 равно
Полученному дифференциальному уравнению соответствует характеристическое уравнение следующего вида
 |
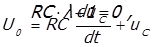где λ — корень характеристического уравнения: λ =-1/RC.
Общее решение будет в виде суммы двух составляющих:
uС = u' + u"
где u' — составляющая соответствующая установившемуся режиму;
u" — составляющая, которой соответствует свободный процесс.
Т.к. u' это установившийся режим при котором u'=U0, таким образом, I'=0.
 |
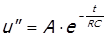Для того чтобы определить вторую составляющую u" нам необходимо решить однородное дифференциальное уравнение, которому соответствует следующее выражение
 |
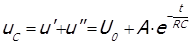Итак, мы пришли к решению общего вида
 |
Найдем константу А из начальных условий, т.е. при t=0:
 |
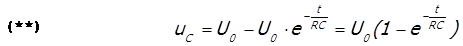После преобразований, получаем
где RC — постоянная времени, равная промежутку времени, по истечению которого напряжение в цени изменяется в е раз, по сравнению со своим исходным напряжением U0.
 |
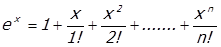Зная, что eх можно разложить в ряд Тейлора
 |
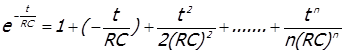который для нашего случая примет следующий вид
Ограничимся двумя первыми членами разложения.
 |
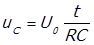Подставляя полученное разложение в формулу (**) получаем
Таким образом, конечный вид формулы будет следующий
 |
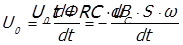Итак, из предыдущих рассуждений следует, что входное напряжение U0 равно скорости изменения магнитного потока Ф через контур (вторичная обмотка экспериментального образца). В свою очередь магнитный поток Ф есть произведение магнитной индукции В на площадь контура S. Иначе говоря, можно записать
 |
или
где S — площадь контура (поперечное сечение магнитопровода);
ω — количество витков охватываемых контуром (в данном случае ω = ω 2 ).
|
Напряженность магнитного поля в данном способе рассчитывается аналогичным образом
Исходя из полученных зависимостей, можно произвести исследование магнитных свойств ферромагнитных материалов, т.е. благодаря электронному осциллографу получаем на экране экспериментальную зависимость В от Н (петлю гистерезиса), по которой затем определяем напряженности (максимальную и коэрцитивную силу) и магнитные индукции (максимальную и остаточную) поля, а также можно определить магнитную проницаемость μ данного материала.