
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Производная функции (40 тестов)
|
|
3.2.1.1/1
Мгновенная скорость материальной точки, движущейся прямолинейно по закону  в момент t=1 равна
в момент t=1 равна
Ответ 18
УС 3
Время 1
3.2.1.1/2
Угол наклона к оси абсцисс касательной к графику функции  в точке с абсциссой
в точке с абсциссой  равен (в градусах)
равен (в градусах)
Ответ 45
УС 3
Время 1
3.2.1.1/3
Производной функции  называется:
называется:
1.  2.
2.  3.
3. 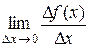 4.
4.  5.
5. 
УС 2
Время 1
3.2.1.2/1
Соответствие производных функций
1 пара 

2 пара 

3 пара 

4 пара 

УС 2
Время 1
3.2.1.2/2
Производная произведения двух функций  равна
равна
1.  2.
2.  3.
3. 
+4.  5.
5. 
УС 2
Время 1
3.2.1.2/3
Производная частного двух функций  равна
равна
1.  +2.
+2.  3.
3. 
+4.  5.
5. 
УС 2
Время 1
3.2.1.3/1
Соответствие функций и их производных
1-я пара:  ;
; 
2-я пара:  ;
; 
3-я пара:  ;
; 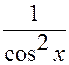
4-я пара:  ;
; 
УС 2
Время 1
3.2.1.3/2
Соответствие функций и их производных
1-я пара:  ;
; 
2-я пара:  ;
; 
3-я пара:  ;
; 
4-я пара:  ;
; 
УС 2
Время 1
3.2.1.3/3
Соответствие функций и их производных
1-я пара:  ;
; 
2-я пара: 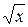 ;
; 
3-я пара:  ;
; 
4-я пара:  ;
; 
УС 2
Время 1
3.2.1.4/1
Произведение производных функции  и ее обратной функции
и ее обратной функции 
 равно:
равно:
+1. 1 2. -1 3. 0 4. постоянной величине
УС 2
Время 1
3.2.1.5/1
Производная сложной функции  равна
равна
1.  2.
2.  +3.
+3.  4.
4.  5.
5. 
УС 4
Время 1
3.2.1.5/2
Производная сложной функции  равна
равна
1.  +2.
+2.  3.
3.  4.
4.  5.
5. 
УС 4
Время 1
3.2.1.5/3
Производная сложной функции  равна
равна
+1.  2.
2.  3.
3.  4.
4.  5.
5. 
УС 4
Время 1
3.2.1.5/4
Производная сложной функции  равна
равна
1.  +2.
+2.  3.
3.  4.
4.  5.
5. 
УС 4
Время 1
3.2.1.5/5
Производная сложной функции  равна
равна
1.  2.
2.  +3.
+3.  4.
4.  5. 1
5. 1
УС 4
Время 1
3.2.1.5/6
Производная сложной функции  равна
равна
1.  2.
2.  3.
3.  +4.
+4.  5. 1
5. 1
УС 4
Время 1
3.2.1.5/7
Производная сложной функции  равна ирррррррррррррррр
равна ирррррррррррррррр
1.  2.
2.  3.
3.  +4.
+4.  5. -2
5. -2
УС 5
Время 1
3.2.1.5/8
Производная функции  в точке
в точке  равна
равна
Ответ -32
УС 5
Время 1
3.2.1.6/1
Производная функции, заданной параметрически  , равна
, равна
1.  +2.
+2.  3.
3.  4.
4. 
УС 4
Время 1
3.2.1.6/2
Производная функции, заданной параметрически  , равна
, равна
+1.  2.
2.  3.
3.  4.
4. 
УС 5
Время 1
3.2.1.7/1
Производная функции, заданной неявно  , равна
, равна
1.  2.
2.  +3.
+3.  4.
4. 
УС 4
Время 1
3.2.1.7/2
Производная функции, заданной неявно  , равна
, равна
1.  2.
2.  3.
3.  +4.
+4. 
УС 4
Время 1
3.2.1.7/3
Производная функции 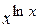 , равна
, равна
1.  +2. 2
+2. 2  3.
3. 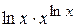 4.
4. 
УС 5
Время 3
3.2.1.7/4
Производная функции  , равна
, равна
1.  2.
2.  3.
3. 
+4. 
УС 5
Время 3
3.2.1.8/1 Теорема Лагранжа для непрерывной на интервале  и дифференцируемой на
и дифференцируемой на  функции
функции  утверждает, что существует точка
утверждает, что существует точка  , такая, что:
, такая, что:
1.  2.
2.  +3.
+3. 
4. 
УС 5
Время 1
3.2.1.8/2 Функции, удовлетворяющие условиям теоремы Лагранжа:
+1. 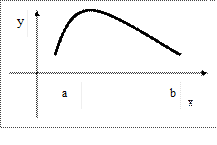 2.
2. 
3.  +4.
+4. 
УС 4
Время 1
3.2.1.10/1 Функции, удовлетворяющие условиям теоремы Ролля:
+1.  2.
2. 
3.  +4.
+4. 
УС 4
Время 1
3.2.1.11/1
Производная второго порядка от функции  равна
равна
1.  + 2.
+ 2. 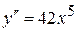 3.
3.  4.
4. 
УС 3
Время 1
3.2.1.11/2
Производная второго порядка от функции  равна
равна
1. cos3x 2. 3cos3x 3. 9sin3x +4. -9sin3x
УС 3
Время 1
3.2.1.11/3
Производная второго порядка от функции  равна
равна
+1. -9cos3x 2. 3cos3x 3. 9sin3x 4. -9sin3x
УС 3
Время 1
3.2.2.1/1
Необходимые условия достижения функцией  экстремума в точке х0:
экстремума в точке х0:
1.  +2.
+2.  3.
3.  4.
4. 
УС 3
Время 1
3.2.2.1/2
Достаточные условия достижения функцией  максимума в точке х0:
максимума в точке х0:
1.  +2.
+2. 
3.  4.
4. 
УС 3
Время 1
3.2.2.1/3
Достаточные условия достижения функцией  минимума в точке х0:
минимума в точке х0:
1.  +2.
+2. 
3.  4.
4. 
УС 3
Время 1
3.2.2.2/1
Функция  возрастает на интервале [a, b], если производная этой функции на этом интервале:
возрастает на интервале [a, b], если производная этой функции на этом интервале:
1.  постоянна 2.
постоянна 2.  3.
3.  +4.
+4. 
УС 3
Время 1
3.2.2.2/2
Функция  убывает на интервале [a, b], если производная этой функции на этом интервале:
убывает на интервале [a, b], если производная этой функции на этом интервале:
1.  постоянна 2.
постоянна 2.  +3.
+3.  4.
4. 
УС 3
Время 1
3.2.2.3/1
Точку перегиба на интервале [-1, 1] имеет функция
1. y=x2 +2. y=x3 3. y= 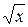 4. y=2x+5 5. y=ex
4. y=2x+5 5. y=ex
УС 4
Время 2
3.2.2.3/2
Точку перегиба на интервале [-1, 1] имеет функция
1. y=2x2 2 y=  3.. y= x3 4. y=3x-4 5. y=lnx
3.. y= x3 4. y=3x-4 5. y=lnx
УС 4
Время 2
3.2.2.3/3
Точка перегиба функции
1.отделяет участок возрастания функции от участка убывания
+2. отделяет участок вогнутости функции от участка выпуклости
3. совпадает с точкой экстремума
4. точка, в которой функция обращается в ноль
УС 4
Время 1
3.2.2.4/1
Вертикальную асимптоту х=3 имеет функция
1.  2.
2.  3.
3.  4.
4. 
УС 3
Время 1
3.2.2.4/2
Вертикальную асимптоту х=0 имеет функция
1.  2.
2.  3.
3.  4.
4. 
УС 3
Время 1