Терморезисторов

2.1. При низкой температуре терморезисторы имеют практически нулевую электропроводность. Все электроны находятся на атомных оболочках, т.е. в " валентной зоне". Обозначим концентрацию электронов в " валентной зоне" N₀.

С ростом температуры увеличиваются амплитуды колебаний атомов, происходят соударения и в результате электроны приобретают энергию, достаточную для отрыва с атомных оболочек, т.е. энергию активации W.

Концентрация свободных электронов N в терморезисторе определяется формулой:

N = N₀ exp() (1)

где: k – постоянная Больцмана; T - температура.

Отметим, что формула (1) показывает: чем выше энергия активации W при заданной температуре T, тем меньше число свободных электронов N. И, наоборот, чем выше температура T при заданной энергии W, тем больше электронов становятся свободными, отрываясь с атомных оболочек. Для расчёта формул, определяющих электропроводность σ и электросопротивление R терморезистора, используем два выражения для плотности тока j:

(2)

Здесь: q – заряд электрона; < V> - средняя скорость направленного движения электронов в электрическом поле с напряжённостью E; N - концентрация электронов в " зоне проводимости".

Из (2) получаем:

σ =N·q·U, (3)

где: U = – подвижность электронов, имеющая постоянную величину.

Удельное электросопротивление ρ является величиной, обратной электропроводности. Учитывая это определение и формулы (1), (3), получим:

(4)

Величина полного электросопротивления равна:

R = (5)

где: L, S - длина и площадь сечения тела, по которому протекает электрический ток. Подставляя в (5) формулу (4), запишем:

R = β 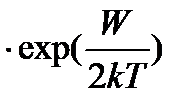(6)

где – постоянный коэффициент.

2.2. Применим теперь формулу (6) для вывода выражения, определяющего энергию активации W на основе данных эксперимента. Пусть при некоторой начальной (комнатной) температуре T₀ сопротивление терморезистора равно:

R₀ = β (7)

Разделив почленно (6) на (7), имеем:

(8)

Логарифмируя (8), получаем:

2kT₀ ln 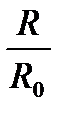= W (9)

Или Y = W·X, (10)

где Y = 2kT₀ |ln 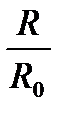|; X = .

Здесь взяты модули разности температур и логарифма, т.к. в опыте температура растёт (T₀ – T < 0), а сопротивление R уменьшается (ln 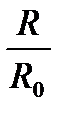< 0).

Из формулы (10) следует, что энергия активации (ширина " запрещённой зоны") равна: W = Y/X, где Y, X вычисляются на основе результатов прямых измерений температуры и сопротивления терморезистора. Среднее значение W обычно определяется по наклону графической зависимости: Y = f(X), при этом на вертикальной оси отсчитывают значения Y (размерность - [ эВ ]), на горизонтальной – значения X (безразмерная величина). Величину W принято измерять в единицах эВ, употребляемых в физике для расчётов энергий, характеризующих состояние элементарных частиц, а также атомных и молекулярных структур.

Примечание. В формулах (9), (10) постоянная Больцмана

ķ = 1, 381·10^-23 Дж/K должна быть преобразована к размерности эВ/К; с учётом того, что 1 эВ = 1, 602·10^-19 Дж, получаем: ķ = 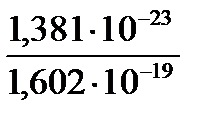= 8, 62·10^-5 .

2.3.В качестве терморезисторов могут использоваться как собственные, так и примесные полупроводники.

Собственный полупроводник – это специально подобранное вещество либо из одного химически чистого элемента (например, германия, кремния, селена и т.п.), либо из одного и того же химического соединения (например, карбида кремния SiC, арсенида галлия GaAs и т.д.). Собственные полупроводники характеризуются постоянной энергией активации W, необходимой для переброса электронов из собственной " валентной зоны" в " зону проводимости". Графическая зависимость Y = f (X), построенная с учётом формулы (10) для собственного полупроводника, представляет собой прямую линию постоянного наклона, определяющего постоянное значение энергии W.

Примесные полупроводники получают добавлением специальных примесей, атомы которых образуют так называемые донорные уровни энергии электронов – промежуточные между основной " валентной зоной" и " зоной проводимости". При этом появляется дополнительная, донорная " валентная зона", уменьшающая начальную энергию активации, что позволяет увеличить число свободных электронов при невысоких температурах. Для изготовления терморезисторов на основе примесных полупроводников обычно используются комбинации элементов типа кобальта, меди, марганца, никеля и др.

Формула (1) для концентрации свободных электронов N в примесных полупроводниках преобразуется к виду:

N = N₀₁exp(- ) + N₀₂exp(- 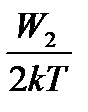) (11)

Здесь N₀₁ и N₀₂ – концентрации электронов в донорной " валентной зоне" и в основной " валентной зоне"; W₁ и W₂ - энергии активации, необходимые для переброса электронов в " зону проводимости" из донорной и основной " валентных зон".

Энергия активации W₁ < W₂. Следовательно, при повышении температуры концентрация свободных электронов N и электропроводность σ вначале увеличиваются за счёт электронов донорной " валентной зоны" с начальной концентрацией N₀₁ и энергией активации W₁.

При дальнейшем росте температуры начинается переброс электронов из основной " валентной зоны" с концентрацией N₀₂ при более высокой энергии активации W₂. Соответствующий этому процессу график Y = f (X) будет представлять собой комбинацию двух линейных зависимостей, имеющих разные наклоны, определяющие значения энергий W₁ и W₂.