
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВНИМАНИЕ. Полученные таким путем значения случайных величин изменяются в ячейках таблицы при каждом пересчете.
|
|
Полученные таким путем значения случайных величин изменяются в ячейках таблицы при каждом пересчете.
Более простые по сравнению с законами распределения способы описания случайных величин связаны с использованием их статистических характеристик: среднего значения, дисперсии, среднеквадратичного отклонения, медианы, моды, квартиля, скоса и т. д.
Рассмотрим случайную величину X — ежедневное количество покупателей в некотором магазине. Пусть х1, х2..... хп — это фактически подсчитанные количества покупателей соответственно в первый, второй,..., n-й день проведения подсчетов. Такую группу фактически измеренных значений случайной величины принято называть выборкой. Среднее значение случайной величины X (обозначается как < х> или М [Х]) по имеющейся выборке вычисляют с помощью формулы;
< x> = 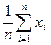
Таблица 13.7. Замеры количества покупателей в магазине № 1
| №п/п | День недели | Условное обозначение | Количество покупателей | (хi - < х>)2 | |
| Понедельник Вторник Среда Четверг Пятница Суббота Воскресенье Итого | x1 x2 x3 x4 xs x6 x7 | 40*40=1600 20*20=400 (-20)*(-20)=400 50*50=2500 (-10)*(-10)=100 (-30)*(-30)=900 (-50)*(-50)=2500 | |||
Пусть, например, замеры количества покупателей в течение недели в магазинах № 1 и № 2 дали результаты, представленные в табл. 13.7 и 13.8 соответственно. Обозначим ежедневное количество покупателей в первом магазине как случайную величину X, а ежедневное количество покупателей во втором магазине как случайную величину Y. По приведенным в таблицах данным видно, что в среднем вдень в каждом из рассматриваемых магазинов бывает 700/7=100 покупателей, то есть < x> =100 и < y> =100.
Таблица 13.8. Замеры количества покупателей в магазине № 2
| №п/п | День недели | Условное обозначение | Количество покупателей | (у, -< у>)2 |
| Понедельник Вторник Среда Четверг Пятница Суббота Воскресенье Итого | y1 yг y3 y4 y5 y6 y7 | 1*1=1 (-2)*(-2)=4 0*0=0 2*2=4 (-3)*(-3)=9 3*3=9 (-1)*(-1)=1 |
Средние величины используются при решении довольно широкого спектра задач экономического анализа. Рассмотрим, например, применение средних для определения уровня сезонности явлений (так называемой «сезонной волны»). Под сезонностью понимают изменения показателей величин, вызванные различными объективными факторами сезонного характера (например, такими факторами могут выступать смена времен года или изменения природно-климатических условий). В качестве показателей сезонности обычно применяют индексы сезонности. Наиболее часто для определения индексов сезонности применяют метод простой средней. В этом случае индекс сезонности  вычисляют по следующей формуле:
вычисляют по следующей формуле:
 ,
,
где  — среднее по определенному периоду времени (месяц, квартал), взятое в течение t лет;
— среднее по определенному периоду времени (месяц, квартал), взятое в течение t лет;  — общее среднее, взятое за общее число периодов времени, п — число анализируемых периодов,
— общее среднее, взятое за общее число периодов времени, п — число анализируемых периодов, 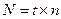 ,
, 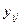 — наблюдавшиеся значения случайной величины. Пусть, например, ведутся помесячные наблюдения (период — месяц, число периодов n=12) за продажей некоторого товара в течение трех лет (t=3,
— наблюдавшиеся значения случайной величины. Пусть, например, ведутся помесячные наблюдения (период — месяц, число периодов n=12) за продажей некоторого товара в течение трех лет (t=3, 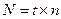 =36). Тогда i - это порядковый номер месяца, j -порядковый номер года наблюдения,
=36). Тогда i - это порядковый номер месяца, j -порядковый номер года наблюдения, 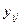 - количество единиц товара проданных в i -м месяце j -го года. Чтобы рассчитать индекс сезонности, скажем, января, нужно найти среднее число продаж только по январям за срок наблюдения и поделить на общее среднее по всем месяцам всего срока.
- количество единиц товара проданных в i -м месяце j -го года. Чтобы рассчитать индекс сезонности, скажем, января, нужно найти среднее число продаж только по январям за срок наблюдения и поделить на общее среднее по всем месяцам всего срока.
Среднее значение можно трактовать как своеобразную середину области возможных значений случайной величины. Важно также знать, как сильно значения изучаемой величины отличаются от ее среднего, насколько кучно размещаются измеренные значения вокруг среднего значения или, иначе говоря, насколько широк разброс случайной величины. Разброс или рассеивание случайной величины вокруг ее среднего характеризуется параметром, который называется дисперсией D[X] случайной величины X. Чем больше дисперсия, тем больше разброс возможных значений случайной величины. Чтобы наглядно представить себе смысл этой величины, рассмотрим следующий пример. Имеются две группы сотрудников некоторой организации. В каждой группе по три человека. Зарплаты сотрудников первой группы: 1000 рублей, 6000 рублей и 11 000 рублей, зарплаты сотрудников во второй группе: 5800 рублей, 6000 рублей и 6200 рублей. В среднем сотрудники каждой из групп получают по 6000 рублей. А теперь сравните отклонения от средней величины в первой и во второй группах. Очевидно, что во второй группе сотрудники получают примерно одинаковую зарплату, отклонения от средней величины незначительны, дисперсия мала. А в первой группе очень велик разброс между уровнями зарплаты, отклонения от средней величины большие, дисперсия велика. Итак, дисперсия характеризует степень отклонения возможных значений случайной величины относительно среднего. Для вычисления значения дисперсии случайной величины X используют следующую формулу:
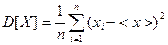 .
.
На практике часто используют и другую характеристику рассеивания - среднеквадратичное отклонение σ х, вычисляемое по формуле  . Величина σ х также характеризует размах колебаний случайной величины X около среднего значения, но среднеквадратичное отклонение σ х, в отличие от дисперсии D[X], имеет ту же размерность, что и случайная величина X.
. Величина σ х также характеризует размах колебаний случайной величины X около среднего значения, но среднеквадратичное отклонение σ х, в отличие от дисперсии D[X], имеет ту же размерность, что и случайная величина X.
Вновь обратимся к рассматриваемому примеру. Так, в магазине № 1 (см. данные последнего столбца табл. 13.7) в среднем количество покупателей каждый день отличается от средней величины (100 человек в день) на 35 человек (так как D[X]= 8400/7=1200 и 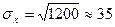 ). В магазине же № 2 (см. данные последнего столбца табл. 13.8) в среднем количество покупателей каждый день отличается от средней величины (100 человек в день) на 2 человека (так как D[X]=28/7=4 и
). В магазине же № 2 (см. данные последнего столбца табл. 13.8) в среднем количество покупателей каждый день отличается от средней величины (100 человек в день) на 2 человека (так как D[X]=28/7=4 и  ). Таким образом, в нашем примере разброс случайной величины X (количество покупателей в магазине №1) около своего среднего значения достаточно велик и составляет приблизительно третью часть средней величины, в то время как разбросом случайной величины Y (количество покупателей в магазине № 2) около ее среднего значения можно пренебречь, так как он составляет всего лишь 2% от средней величины. Исходя из этого, следует определенным образом планировать, например, завоз скоропортящихся продуктов в магазины. В первом магазине в один из дней может оказаться очень мало покупателей, и существует большой риск, что продукция не будет распродана и пропадет, в то время как во втором магазине такой риск очень мал и им можно пренебречь.
). Таким образом, в нашем примере разброс случайной величины X (количество покупателей в магазине №1) около своего среднего значения достаточно велик и составляет приблизительно третью часть средней величины, в то время как разбросом случайной величины Y (количество покупателей в магазине № 2) около ее среднего значения можно пренебречь, так как он составляет всего лишь 2% от средней величины. Исходя из этого, следует определенным образом планировать, например, завоз скоропортящихся продуктов в магазины. В первом магазине в один из дней может оказаться очень мало покупателей, и существует большой риск, что продукция не будет распродана и пропадет, в то время как во втором магазине такой риск очень мал и им можно пренебречь.
Медиана — это статистическая характеристика, которая определяет середину выборки, то есть половина чисел, образующих выборку, имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Не нужно путать среднее с медианой. Так, для магазина № 1 среднее число покупателей, согласно проведенным выше расчетам, равно 70, в то время как медиана равна 90. В самом деле, если выстроить количество покупателей в разные дни недели по возрастанию, то будет получена следующая последовательность: 50, 70, 80, 90, 120, 140, 150. Очевидно, что в этой последовательности три значения 50, 70, и 80 меньше, чем 90, и три значения 120, 140, 150 — больше. Следовательно, 90 является медианой рассматриваемой выборки.
Аналогичный характер имеют характеристики, которые называются квартилями, каждый из них определяет положение четвертой части выборки. Так, первый квартиль — это число, меньше которого 25% выборки. Второй квартиль совпадает с медианой, так как он определяется числом, меньше которого 50% выборки. А третий квартиль определяется числом, меньше которого 75% выборки.
Следующая статистическая характеристика мода определяется как наиболее часто встречающееся в выборке значение случайной величины. Так, в выборке {5, 6, 5, 4, 4, 3, 2, 4} мода равняется 4.
Числовая характеристика, которая называется скос или асимметрия, характеризует степень несимметричности размещения элементов выборки относительно ее среднего значения. Положительный скос свидетельствует о перекосе выборки в сторону больших значений, и наоборот, отрицательный — о перекосе в сторону меньших значений. Так, скос для данных по первому магазину равен 0, 196, а для данных по второму магазину равен 0, следовательно, в первом случае наблюдается положительная асимметрия, а во втором — отсутствует.
Для определения степени однородности случайной величины по формуле 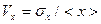 вычисляется ее коэффициент вариации Vx. Если величина V < 0, 33, то совокупность значений случайной величины X можно считать достаточно однородной, в противном случае — неоднородной, состоящей из различных по своему содержанию совокупностей.
вычисляется ее коэффициент вариации Vx. Если величина V < 0, 33, то совокупность значений случайной величины X можно считать достаточно однородной, в противном случае — неоднородной, состоящей из различных по своему содержанию совокупностей.
Для исследования степени связи между двумя различными случайными величинами X и Y определяется мера тесноты связи, которую принято называть коэффициентом корреляции и обозначать rij. Возможные значения коэффициента корреляции находятся в диапазоне от минус единицы до плюс единицы. После вычисления коэффициента корреляции необходимо проанализировать его значение. Принято считать, что между величинами имеется некоторая корреляционная зависимость, если модуль коэффициента корреляции больше, чем 0, 1. При | rxy |> 0, 3 корреляционная связь признается существенной, при | rxy |> 0, 5 — значительной, а при | rxy |> 0, 7 -тесной. Если величина коэффициента корреляции близка к единице, то можно считать, что между случайными величинами имеется прямая причинно-следственная связь. Если коэффициент корреляции близок к минус единице, то это свидетельствует об обратной зависимости исследуемых величин. При коэффициенте корреляции, близком к 0, можно считать, что связь между величинами отсутствует.
Для вычисления рассмотренных и многих других статистических характеристик случайных величин программа MS Excel располагает широким набором статистических функций. Их полный список можно получить, выполнив команду Вставка > Функция.... Программа MS Excel предусматривает также применение 18 статистических инструментов анализа, в том числе таких, как описательная статистика, гистограмма, генерация случайных чисел, корреляция и ряд других. Эти инструменты позволяют автоматизировать статистический анализ данных. Доступ к ним можно получить, выполнив команду Сервис > Анализ данных.... Затем в диалоговом окне Анализ данных в списке Инструменты анализа следует выбрать нужный инструмент и задать входной и выходной интервалы, а также другие требуемые параметры. Например, инструмент анализа Описательная статистика создает список рассмотренных выше статистических характеристик записанной в некотором диапазоне ячеек выборки. При помощи этого инструмента можно получить информацию об основной тенденции и изменчивости данных. В частности, можно вычислить следующие характеристики: дисперсию выборки, среднеквадратичное отклонение, медиану, моду и скос.
Если в меню Сервис отсутствует команда Анализ данных..., это свидетельствует о том, что инструменты анализа статистических данных не установлены в MS Office. В этом случае следует выполнить команду Сервис > Надстройки... и в списке надстроек окна команды включить флажок в строке Пакет анализа, нажав затем кнопку ОК.