
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оптимальный выбор 2 страница
|
|
Что бы вы подумали о человеке, который заявил, что предпочитает набор X набору Y и набор Y набору Z, а затем заявил также, что предпочитает набор Z набору X? Это, безусловно, было бы расценено как свидетельство весьма странного поведения.
Еще важнее следующее: как повел бы себя такой потребитель при выборе из трех наборов X, Y и Z? Если бы мы попросили его выбрать самый предпочитаемый им набор, перед ним возникла бы серьезная проблема, ведь какой бы набор он ни выбрал, всегда будет существовать набор, который он бы предпочел выбранному. Если мы хотим иметь теорию, в рамках которой люди осуществляют " наилучший" выбор, то предпочтения должны удовлетворять аксиоме транзитивности или чему-то в подобном роде. Если бы предпочтения не были транзитивны, вполне могло бы существовать множество наборов, выбрать наилучший из которого невозможно.
3.3. Кривые безразличия
Оказывается, всю теорию потребительского выбора можно сформулировать с позиций предпочтений, удовлетворяющих трем вышеописанным аксиомам, к которым добавляется несколько предпосылок технического характера. Нам, однако, удобно описать предпочтения графически, используя для этого построение, именуемое кривыми безразличия.
Рассмотрим рис.3.1, изображающий две оси, вдоль которых отложено потребление неким потребителем товаров 1 и 2. Выберем определенный потребительский набор Ошибка! Не указан аргумент ключа. (x 1, x 2) Ошибка! Не указан аргумент ключа. и заштрихуем область всех потребительских наборов, слабо предпочитаемых набору (x 1, x 2) Ошибка! Не указан аргумент ключа.. Эта область именуется слабо предпочитаемым множеством. Наборы, лежащие на границе этого множества, — те, которые столь же хороши для данного потребителя, как и набор Ошибка! Не указан аргумент ключа. (x 1, x 2) Ошибка! Не указан аргумент ключа., образуют кривую безразличия.
Мы можем провести кривую безразличия через любой потребительский набор. Кривая безразличия, проходящая через какой-либо потребительский набор, состоит из всех товарных наборов, которые для потребителя не хуже заданного.
Одна из проблем использования кривых безразличия для описания предпочтений состоит в том, что указанные кривые показывают лишь наборы, которые потребитель воспринимает как безразличные друг другу, не показывая при этом, какие наборы лучше, а какие хуже. Полезно иногда рисовать на кривых безразличия маленькие стрелочки, указывающие направление расположения предпочитаемых наборов. Мы не всегда будем это делать, но непременно поступим так в тех примерах, в которых иначе могла бы возникнуть путаница.
Если не ввести никаких дополнительных предпосылок в отношении предпочтений, то кривые безразличия могут принимать весьма странную форму. Однако уже на данном уровне обобщения можно сформулировать важный принцип, характеризующий кривые безразличия: кривые безразличия, представляющие отличные друг от друга уровни предпочтений, не могут пересекаться. Другими словами, ситуация, изображенная на рис. 3.2, не может иметь места в действительности.

| Слабо предпочитаемое множество. Закрашенная область состоит из всех наборов, которые по крайней мере не хуже набора Ошибка! Не указан аргумент ключа.(x 1, x 2)Ошибка! Не указан аргумент ключа.. | Рис. 3.1 |
Чтобы доказать это, выберем три товарных набора, X, Y и Z, таких, что X лежит лишь на одной кривой безразличия, Y — лишь на другой кривой безразличия, а Z — на пересечении указанных кривых безразличия. Согласно сделанному нами предположению кривые безразличия представляют разные уровни предпочтений, так что один из наборов, скажем X, строго предпочитается другому набору, Y. Нам известно, что X ~ Z Ошибка! Не указан аргумент ключа. и что Z ~ Y Ошибка! Не указан аргумент ключа., из аксиомы же транзитивности, поэтому должно следовать, что X ~ Y Ошибка! Не указан аргумент ключа.. Это, однако, противоречит предположению о том, что X f Y Ошибка! Не указан аргумент ключа.. Указанное противоречие дает нам искомый результат — кривые безразличия, представляющие отличные друг от друга уровни предпочтений, не могут пересекаться. Какими другими свойствами обладают кривые безразличия? Отвечая на вопрос абстрактно, — немногими. Кривые безразличия есть способ описания предпочтений. Почти любые мыслимые " разумные" предпочтения могут быть представлены с помощью кривых безразличия. Трудность заключается в том, чтобы узнать, каков вид предпочтений, порождающих те или иные формы кривых безразличия.
3.4. Примеры предпочтений
Попробуем установить связь между предпочтениями и кривыми безразличия с помощью некоторых примеров. Опишем некоторые предпочтения, а затем посмотрим, как выглядят кривые безразличия, их представляющие.

| Рис. 3.2 | Кривые безразличия не могут пересекаться. Если бы они пересекались, наборы X, Y и Z были бы безразличными друг другу, а следовательно, не могли бы лежать на отличных друг от друга кривых безразличия. |
Совершенные субституты
Два товара являются совершенными субститутами, если потребитель готов заместить один товар другим в постоянной пропорции. Простейший случай совершенных субститутов — когда потребитель готов заместить один товар другим в соотношении один к одному.
Предположим, например, что мы выбираем между красными и синими карандашами и что потребитель, совершающий этот выбор, любит карандаши, но совершенно равнодушен к их цвету. Выберем какой-либо потребительский набор, скажем, (10, 10). Тогда для данного потребителя любой другой потребительский набор, содержащий 20 карандашей, столь же хорош, как и набор (10, 10). Выражаясь языком математики, любой потребительский набор (x 1, x 2 Ошибка! Не указан аргумент ключа.), такой, что x 1 + x 2 = 20 Ошибка! Не указан аргумент ключа., будет лежать на кривой безразличия данного потребителя, проходящей через набор (10, 10). Следовательно, все кривые безразличия для данного потребителя представляют собой параллельные прямые линии с наклоном –1, как показано на рис. 3.3. Наборы с бó льшим совокупным числом карандашей предпочитаются наборам с меньшим совокупным числом карандашей, поэтому предпочтения возрастают в направлении вправо вверх, что иллюстрирует рис. 3.3.
Как все это выглядит с точки зрения общей процедуры вычерчивания кривых безразличия? Если мы находимся в точке (10, 10) и увеличиваем количество первого товара на одну единицу до 11, то на сколько нам понадобится изменить количество второго товара, чтобы вернуться на исходную кривую безразличия? Ответ, очевидно, следующий: количество второго товара придется уменьшить на одну единицу. Таким образом, кривая безразличия, проходящая через точку (10, 10), имеет наклон –1. Ту же самую процедуру можно проделать применительно к любому другому товарному набору, получив при этом те же самые результаты, — в данном случае все кривые безразличия будут иметь постоянный наклон, равный –1.
Говоря о совершенных субститутах, важно подчеркнуть, что кривые безразличия имеют постоянный наклон. Предположим, например, что мы взяли случай предпочтений потребителя в отношении синих карандашей и пары красных карандашей. Наклон кривых безразличия для этих двух товаров равен –2, так как потребитель готов уступить два карандаша, чтобы получить еще одну пару красных карандашей.

| Рис. 3.3 | Совершенные субституты. Потребителя интересует лишь общее число карандашей, но не их цвет. Следовательно, кривые безразличия представляют собой прямые линии с наклоном, равным –1. |
В учебнике мы рассмотрим в основном случай, когда два товара выступают совершенными субститутами в соотношении один к одному.
Совершенные комплементы
Совершенные комплементы — это товары, всегда потребляемые вместе в постоянной пропорции. В определенном смысле эти товары друг друга " дополняют". Хорошим примером совершенных комплементов могут служить правый и левый ботинки. Потребитель “любит” ботинки, но при этом всегда носит правый и левый ботинки вместе. Наличие у потребителя всего лишь одного ботинка из пары не способствует его благосостоянию.
Нарисуем кривые безразличия для совершенных комплементов. Предположим, мы выберем потребительский набор (10, 10). Добавив к нему еще 1 правый ботинок, получаем набор (11, 10). Согласно сделанному нами предположению, это не меняет благосостояния потребителя по сравнению с исходной позицией: лишний ботинок не увеличивает его. То же самое произойдет, если добавить к исходному набору еще один левый ботинок: потребителю будет также безразлично, иметь ли набор (10, 11) или (10, 10).
Таким образом, кривые безразличия имеют форму буквы L с вершиной в точке, где количество левых ботинок равно количеству правых ботинок, как на рис.3.4.

| Совершенные комплементы. Потребитель всегда стремится потреблять товары в постоянной пропорции. Поэтому кривые безразличия имеют форму буквы L. | Рис. 3.4 |
Если одновременно увеличить количество левых и правых ботинок, потребитель передвинется в более предпочитаемую точку, так что усиление предпочтений и в этом случае, как показано на графике, происходит в направлении вправо вверх.
Говоря о совершенных комплементах, важно подчеркнуть, что потребитель предпочитает потреблять товары в постоянной пропорции, но при этом не обязательно в пропорции один к одному. Для потребителя, который всегда кладет в чашку чая две чайные ложки сахара, не употребляя сахар больше ни на что, кривые безразличия будут по-прежнему иметь форму буквы L. В этом случае вершины L-образных кривых безразличия будут приходиться уже на точки (2 чайные ложки сахара, 1 чашка чая), (4 чайные ложки сахара, 2 чашки чая) и т.д., а не на точки (1 правый ботинок, 1 левый ботинок), (2 правых ботинка, 2 левых ботинка) и т.д.
В учебнике мы рассмотрим в основном случай, когда товары потребляются в пропорции один к одному.
Антиблага
Антиблаго — это товар, который потребителю не нравится. Пусть, например, речь идет о таких товарах, как стручковый перец и анчоусы, и потребитель любит стручковый перец, но терпеть не может анчоусы. Предположим, однако, что существует некая возможность выбора между стручковым перцем и анчоусами. Иными словами, добавлением в пиццу какого-то количества стручкового перца можно было бы компенсировать потребителю вынужденное потребление заданного количества анчоусов. Как можно представить эти предпочтения, пользуясь кривыми безразличия?
Выберите набор Ошибка! Не указан аргумент ключа. (x 1, x 2), состоящий из некоторого количества стручкового перца и некоторого количества анчоусов. Если дать потребителю больше анчоусов, то что придется сделать со стручковым перцем, чтобы удержать данного потребителя на той же самой кривой безразличия? Разумеется, придется дать потребителю еще сколько-то перца, чтобы компенсировать необходимость мириться с анчоусами. Поэтому кривые безразличия для такого потребителя должны восходить вправо вверх, как показано на рис.3.5.

| Рис. 3.5 | Антиблага. Для этого потребителя анчоусы являются " антиблагом", а стручковый перец — " благом". Поэтому кривые безразличия имеют положительный наклон. |
Предпочтения в данном случае возрастают вправо вниз, т. е. в направлении уменьшившегося потребления анчоусов и увеличившегося потребления стручкового перца, как показывают стрелки на графике.
Безразличные блага
Товар есть безразличное благо, если потребитель к нему совершенно равнодушен. Что, если потребитель просто равнодушен к анчоусам? [1]
В этом случае кривые безразличия для данного потребителя будут вертикальными линиями, подобными изображенным на рис.3.6. Потребителя волнует лишь количество имеющегося у него стручкового перца и совершенно не волнует, сколько у него имеется анчоусов. Чем больше стручкового перца, тем лучше, добавление же анчоусов никак не влияет на его благосостояние.

| Безразличное благо. Потребитель любит стручковый перец, но равнодушен к анчоусам, поэтому кривые безразличия представляют собой вертикальные линии. | Рис. 3.6 |
Насыщение
Иногда возникает необходимость рассмотреть ситуацию, предполагающую насыщение, в которой для потребителя существует некий самый наилучший набор, и чем " ближе" потребитель находится к этому наилучшему набору, тем выше его благосостояние с позиций его предпочтений. Например, предположим, что у потребителя имеется какой-то самый предпочитаемый товарный набор ( Ошибка! Не указан аргумент ключа.) и что чем дальше он находится от этого набора, тем ниже его благосостояние. В этом случае мы говорим, что точка (
Ошибка! Не указан аргумент ключа.) и что чем дальше он находится от этого набора, тем ниже его благосостояние. В этом случае мы говорим, что точка ( Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа. — это точка насыщения, или точка блаженства. Кривые безразличия для данного потребителя выглядят как изображенные на рис.3.7. Самая лучшая точка — точка (
Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа. — это точка насыщения, или точка блаженства. Кривые безразличия для данного потребителя выглядят как изображенные на рис.3.7. Самая лучшая точка — точка ( Ошибка! Не указан аргумент ключа.Ошибка! Не указан аргумент ключа.), а точки, удаляющиеся от этой точки блаженства, лежат на более " низких" кривых безразличия.
Ошибка! Не указан аргумент ключа.Ошибка! Не указан аргумент ключа.), а точки, удаляющиеся от этой точки блаженства, лежат на более " низких" кривых безразличия.
В данном случае наклон кривых безразличия отрицателен, когда у потребителя имеется " слишком мало" или " слишком много" обоих товаров, и положителен, когда у него " слишком много" одного из товаров. В последнем случае этот товар становится антиблагом — сокращение потребления такого товара перемещает потребителя ближе к " точке блаженства". Если у него слишком много обоих товаров, они оба являются антиблагами, и поэтому сокращение потребления каждого из них перемещает потребителя ближе к точке блаженства.

| Рис. 3.7 | Предпочтения в случае насыщения. Набор ( Ошибка! Не указан аргумент ключа.) есть точка насыщения, или точка блаженства, кривые безразличия " окружают" данную точку. Ошибка! Не указан аргумент ключа.) есть точка насыщения, или точка блаженства, кривые безразличия " окружают" данную точку.
|
Допустим, что в роли двух таких товаров выступают шоколадный торт и мороженое. Вполне вероятно, что существует некое оптимальное количество шоколадного торта и мороженого, которое вам хотелось бы съедать еженедельно. Потребление любого количества этих товаров в размерах менее указанного означало бы ухудшение вашего благосостояния, однако и потребление любого их количества сверх указанного также приводило бы к его ухудшению.
Если поразмыслить, то окажется, что в этом отношении большинство товаров подобны шоколадному торту и мороженому — пресытиться можно почти всем. Но обычно люди не стремятся потреблять чрезмерно много одних и тех же товаров. С какой стати вы предпочтете иметь чего-то больше, чем вам хочется? Поэтому, с точки зрения экономического выбора, интерес представляет та область, в которой вы потребляете большинство товаров в количествах меньше желаемых. В действительности людей интересует выбор именно такого рода, и как раз его мы и будем рассматривать.
Дискретные товары
Обычно мы измеряем количество товаров в единицах, для которых дробные части тоже имеют смысл — можно в среднем потреблять 12, 43 галлона молока в месяц, несмотря на то, что каждый раз вы покупаете по кварте молока. Иногда, однако, возникает необходимость исследовать предпочтения в отношении товаров, потребление которых в силу их природы ограничено отдельными целыми единицами.
Например, рассмотрим спрос потребителя на автомобили. Мы могли бы выразить спрос на автомобили во времени, затраченном на пользование автомобилем, получив таким образом непрерывную переменную, однако для многих целей интерес представляет именно спрос, предъявляемый на фактическое число автомобилей.
Использование предпочтений для описания поведения в отношении выбора, касающегося такого рода дискретного товара, трудностей не представляет. Пусть x 2 Ошибка! Не указан аргумент ключа. — деньги, расходуемые на все другие товары, а x 1 Ошибка! Не указан аргумент ключа. — дискретный товар, который можно приобретать только в неделимых количествах. Внешний вид " кривых" безразличия и слабо предпочитаемое множество для товара такого рода показаны на рис.3.8. В этом случае наборы, безразличные данному, будут множеством отдельных точек. Множество же наборов, по крайней мере не худших, чем данный конкретный набор, будет представлено множеством отрезком прямых.

A " Кривые" безразличия B Слабо предпочитаемое множество
| Дискретный товар. В данном случае товар 1 можно приобрести только в неделимых количествах. Пунктирные линии на рис. A соединяют между собой безразличные друг другу наборы, а вертикальные линии на рис. B представляют наборы, по крайней мере не худшие, чем обозначенный набор. | Рис. 3.8 |
Вопрос о том, следует ли подчеркивать дискретную природу какого-либо товара, решается в зависимости от прикладных целей исследования. Если за весь временнó й период, охваченный нашим исследованием, потребитель выбирает одну или две единицы товара, признание дискретной природы выбора может иметь значение. Если же потребитель выбирает 30 или 40 единиц товара, то, возможно, удобнее считать данный товар делимым.
3.5. Стандартные предпочтения
Выше уже рассмотрено несколько примеров кривых безразличия. Как мы видели, с помощью этих простых графиков можно описать многие виды предпочтений, рациональных или нерациональных. Но для того чтобы описать предпочтения в общем виде, удобнее сконцентрировать внимание на нескольких типичных формах кривых безразличия. В настоящем параграфе мы расскажем еще о нескольких предпосылках общего характера, вводимых обычно в отношении предпочтений, и о значении этих предпосылок для формы соответствующих кривых безразличия. Предпосылки эти — не единственно возможные: в некоторых ситуациях, возможно, захочется использовать отличные от них предпосылки. Примем, однако, данные предпосылки в качестве определяющих характерные черты стандартных кривых безразличия.
Во-первых, будем считать, что чем товара больше, тем лучше, т. е. что речь идет о благах, а не об антиблагах. Выражаясь более точно, если (х 1, х 2 Ошибка! Не указан аргумент ключа.) — один товарный набор, а (y 1, y 2 Ошибка! Не указан аргумент ключа.) — другой товарный набор, в котором обоих товаров по крайней мере не меньше, чем в Ошибка! Не указан аргумент ключа. (х 1, х 2 Ошибка! Не указан аргумент ключа.), а одного из них — больше, то (y 1, y 2 Ошибка! Не указан аргумент ключа.) f (х 1, х 2 Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа.. Эту предпосылку иногда называют аксиомой монотонности предпочтений (или аксиомой ненасыщения — прим. науч. ред.). Как мы предположили в ходе обсуждения проблемы насыщения, утверждение " чем больше, тем лучше" справедливо, возможно, лишь до определенного предела. Следовательно, предпосылка о монотонности предпочтений говорит лишь о том, что мы намереваемся исследовать ситуации выбора до наступления указанного предела, до того, как обнаружится какое-либо насыщение — пока " больше" все еще означает " лучше". Экономическая теория была бы не очень-то интересным предметом в мире, где люди достигли точки насыщения в потреблении каждого товара.
Что означает монотонность предпочтений применительно к форме кривых безразличия? Она означает, что эти кривые будут иметь отрицательный наклон. Посмотрим на рис.3.9. Если взять за исходный набор (х 1, х 2 Ошибка! Не указан аргумент ключа.) и двигаться от него в любую точку вправо вверх, то тем самым мы будем перемещаться в более предпочитаемое положение. Двигаясь влево вниз, будем перемещаться в худшее положение. Поэтому чтобы перемещаться, не изменяя благосостояния, мы должны двигаться либо влево вверх, либо вправо вниз: кривая безразличия должна иметь отрицательный наклон.

| Монотонные предпочтения. Для данного потребителя лучше тот набор, в котором обоих товаров больше; а хуже тот, в котором обоих товаров меньше. | Рис. 3.9 |
Во-вторых, примем предпосылку о том, что средние значения предпочитаются крайним. Другими словами, если взять два товарных набора, (х 1, х 2 Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа. и (y 1, y 2 Ошибка! Не указан аргумент ключа.), лежащих на одной и той же кривой безразличия, и такое взвешенное среднее этих двух наборов, что
 Ошибка! Не указан аргумент ключа.
Ошибка! Не указан аргумент ключа.
то средний набор будет по крайней мере не хуже каждого из двух крайних либо будет строго им предпочитаться. Этот средневзвешенный набор содержит среднее количество товара 1 и среднее количество товара 2, имеющееся в двух наборах. Поэтому он лежит посередине отрезка прямой, соединяющего x -набор и y -набор.
В действительности будем считать сказанное справедливым для любого весового коэффициента t, принимающего значения от 0 до 1, а не только для 1/2. Таким образом, мы полагаем, что если (х 1, х 2 Ошибка! Не указан аргумент ключа.) ~ (y 1, y 2 Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа., то для любого t, такого, что 0 £ t £ 1, будет Ошибка! Не указан аргумент ключа.
(tx 1 + (1 — t) y 1, tx 2 + (1 — t) y 2) 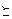 (x 1, x 2). Ошибка! Не указан аргумент ключа.
(x 1, x 2). Ошибка! Не указан аргумент ключа.
В этой средневзвешенной двух наборов x -набор имеет вес t, а y -набор — вес 1– t. Следовательно, расстояние от x -набора до среднего набора есть просто t -я доля расстояния от x -набора до y -набора вдоль прямой, соединяющей два указанных набора.
Геометрический смысл данного предположения в отношении предпочтений состоит в том, что множество наборов, слабо предпочитаемых набору (х 1, х 2 Ошибка! Не указан аргумент ключа.) Ошибка! Не указан аргумент ключа.Ошибка! Не указан аргумент ключа., есть выпуклое множество. Пусть (y 1, y 2 Ошибка! Не указан аргумент ключа.) и (х 1, х 2 Ошибка! Не указан аргумент ключа.) — безразличные друг другу наборы. Тогда, если средние значения предпочитаются крайним, то все средневзвешенные наборов (х 1, х 2 Ошибка! Не указан аргумент ключа.) и (y 1, y 2 Ошибка! Не указан аргумент ключа.) слабо предпочитаются наборам (х 1, х 2 Ошибка! Не указан аргумент ключа.) и (y 1, y 2 Ошибка! Не указан аргумент ключа.). Выпуклое множество обладает тем свойством, что если взять любые две принадлежащие ему точки и провести отрезок прямой, их соединяющий, то указанный отрезок будет полностью лежать внутри данного множества.
На рис.3.10A изображен пример выпуклых предпочтений (здесь и везде в тексте под выпуклыми предпочтениями понимаются предпочтения, изображаемые кривыми безразличия, выпуклыми к началу координат — прим. науч. ред.), а на рис.3.10B и 3.10C показаны два примера невыпуклых предпочтений. На рис.3.10C представлены предпочтения, которые невыпуклы до такой степени, что хочется назвать их " вогнутыми" предпочтениями (и снова имеется в виду вогнутость соответствующих кривых безразличия относительно начала координат — прим. науч. ред.).

A Выпуклые B Невыпуклые C Вогнутые
предпочтения предпочтения предпочтения
| Рис. 3.10 | Различные виды предпочтений. На рис.A изображены выпуклые предпочтения, на рис.B — невыпуклые предпочтения и на рис.C — " вогнутые" предпочтения. |
Можно ли представить себе предпочтения, которые не были бы выпуклыми? Одним из возможных примеров таких предпочтений могли бы стать мои собственные предпочтения в отношении мороженого и оливок. Я люблю мороженое и люблю оливки... но не люблю есть их вместе! О моем потреблении в течение ближайшего часа можно сказать следующее: мне, возможно, безразлично, съесть 8 унций мороженого и 2 унции оливок или же 2 унции мороженого и 8 унций оливок, но любой из этих наборов для меня лучше, чем одновременное потребление 5 унций того и другого! Именно такого рода предпочтения представлены на рис.3.10C.
Почему мы стремимся принять предпосылку о том, что стандартные предпочтения выпуклы? Потому что по большей части товары потребляются совместно. Предпочтения видов, представленных на рис.3.10B и 3.10C, подразумевают, что потребитель предпочел бы по крайней мере до некоторой степени специализироваться на потреблении лишь одного из товаров. Однако нормальным является случай, когда потребитель готов обменять некоторое количество одного товара на другой и потреблять в конечном счете некоторое количество каждого из товаров, а не специализироваться на потреблении лишь одного из двух товаров.
В самом деле, если взглянуть не на мое потребление в данный момент, а на мои предпочтения в отношении ежемесячного потребления мороженого и оливок, то мы увидим, что они гораздо более похожи на рисунок 3.10A, чем на рисунок 3.10C. Я предпочел бы ежемесячно потреблять сколько-то мороженого и сколько-то оливок, хотя и в разное время, нежели специализироваться на потреблении какого-то одного из этих товаров в течение всего месяца.
Наконец, развитием предпосылки о выпуклости предпочтений является предпосылка о строгой выпуклости предпочтений (именуемая также аксиомой строгой выпуклости предпочтений — прим. науч. ред.). Она означает, что средневзвешенная двух различных наборов строго предпочитается двум крайним наборам. Кривые безразличия для выпуклых предпочтений могут иметь участки, представленные отрезками прямых, в то время как строго выпуклые предпочтения должны описываться " скругленными" кривыми безразличия. Предпочтения в отношении двух товаров, являющихся совершенными субститутами, выпуклы, но не строго выпуклы.