Основные положения. При органицации СМО важно выбрать ее параметры так, чтобы наилучшим образом решать стоящие перед ней задачи

При органицации СМО важно выбрать ее параметры так, чтобы наилучшим образом решать стоящие перед ней задачи. Качество решения в общем случае, как известно, определяется с помощью векторного критерия эффективностей, компонентами которого являются частные показатели функционирования СМО.

Решение задачи поиска рациональных параметров СМО на основе векторного критерия требует специальных подходов, и здесь мы их рассматривать не будем.

Весьма распространенным способом оптимизации параметров СМО, допускающим регулярных методов оптимизации, является сведение векторного критерия к скалярному (так называемая свертка векторного критерия). В большом числе случаев такой подход является вполне естественным и скалярный критерий с выбранной точки зрения полностью отражает качество функционирования СМО.

Рассмотрим функционал:

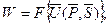
где 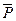- вектор параметров системы; 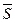- вектор, характеризующий состояние внешний среды; 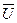- вектор частных показателей функционирования СМО.

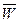называют целевой функцией, скалярным критерием эффективности, интегральным показателем эффективности, интегральным показателем эффективности СМО и т.п.

При записи (4.1) сделано предложение, что в процессе функционирования СМО никакие управления не вводятся и результаты функционирования полностью определяются параметрами СМО и состоянием внешней среды.

Применительно к Марковским СМО, рассматриваемым в курсе, векторы 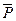и 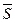получают очень простой вид:

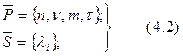
где i-индекс приоритета.

С учетом (4.2) можно переписать (4.1) в виде

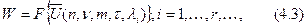
где F имеет смысл оператора свертывания частных показателей эффективности в интегральный.

Задачу оптимизации параметров СМО можно сформировать следующим образом:

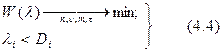
где 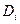- некоторое i-е дисциплинирующее условие, определяемое спецификой задачи.

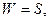
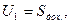
В качестве примера рассмотрим оптимизацию параметров парикмахерской. Здесь в качестве интегрального критерия разумно испытывать величину прибыли S, которая определяется, с одной стороны, доходами от обслуживания клиентов Sдох. и расходами Sрасх. на содержание парикмахерской, с другой стороны. Здесь 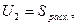оператор F имеет смысл выполнения работы.

Частные показатели задаются функциями

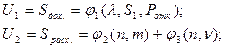
где 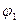- средняя плата за обслуживание одного клиента; 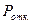- вероятность отказа в обслуживании; 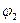- плата за содержание помещения, зависящая от числа сотрудников и допустимой длины очереди (монотонно возрастающая функция); 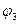- заработная плата, зависящая от квалификации парикмахеров и монотонно возрастающая.

Данная задача (4.4) получает вид:

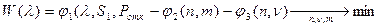
Исследование можно сделать интересней, если ввести зависимость 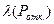и прогрессивное обложение налогом .

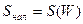Стоимостной критерий широко распространен, но он не является универсальным. Например, если исследовать с помощью аппарата ТМО систему ПВО, то стоимость ее может выступать лишь в качестве ограничения, а показателем функционирования будет естественно принять, скажем, математическое ожидание числа проникших самолетов противника, или (в терминах ТМО) вероятность отказа в обслуживании:

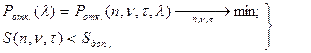
где τ -время пребывания цели в зоне ПВО, зависящее от глубины зоны ответственности.

Варианты заданий

1. Оптимизировать число линий связи и исследовать время окупаемости от

интенсивности поступающих вызовов λ. При расчетах полагать:

среднее время τ 1 разговора – в единицах времени;

обслуживание одного разговора приносит среднюю прибыль в S_прб. условных единиц;

эксплуатация одного работающего канала обходится в S_э условных единиц в единицу

времени;

стоимость S_пр. простоя одного канала – условная в единицу времени;

создание одного канала требует расхода S_созд. единиц.

2. Исследовать целесообразность введения второй, третьей и четвертой технологических линий ремонта сельскохозяйственных машин (с учетом времени окупаемости этих линий) в условиях следующей задачи.

Станция текущего ремонта сельскохозяйственной техники имеет одно помещение, в

котором может ремонтироваться только одна машина (одна технологическая линия). Во дворе станции имеется площадка, где одновременно могут находиться, ожидая ремонта, не более m машин. Статистика времени ремонта в этой мастерской показала, что оно распределено по эксплуатационному закону по средним значением 1/υ суток.

При анализе потока поступающей на ремонт техники было установлено, что этот поток является простейшим с параметром λ машин в сутки. Если площадка для ожидания занята, то машины поступают на другую станцию.

Стоимость оборудования для новой технологической линии составляет S₀ тысяч

рублей, содержание обслуживающего персонала на одной линии – S_сод. рублей в месяц, стоимость простоя сельскохозяйственной машины – S_пр. рублей в сутки. Ремонт одной машины приносит станции доход S_дох. руб.

3. Исследовать зависимость оптимального числа обслуживающих рабочих от их квалификации.

Цех имеет n станков-автоматов. Суточный простой одного станка обходится предприятию в S_пр. руб.Среднее время необходимое для наладки одного станка, может в зависимости от квалификации рабочего принимать значения:

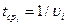
Зарплата рабочих в зависимости от их квалификации составляет соответственно S рублей в месяц.

Интенсивность отказов станков λ.

4. Исследовать с точки зрения минимизации простоя судов 3 варианта проекта морского

порта с возможными грузооборотами 2, 3 и 4 млн. тонн в год, если суда, прибывающие в порт, имеют грузоподъемность до 20 тыс. т. Статистика показала, что поступающие для разгрузки в порт суда образуют поток, близкий к пуассоновскому, с параметром 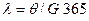, где θ - грузооборот порта, а G – средняя грузоподъемность принимаемых портом судов. Длительность погрузочно-разгрузочных работ принять распределенной

по экспоненциальному закону с математическим ожиданием 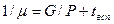, где P – пропускная способность одного причала; t_всп. – время на вспомогательные операции с судном у причала.

5. Аэродром имеет две посадочные полосы. Время занятости каждой из них садящимся

самолетом распределено экспоненциально со средним значением 1/υ (оцените допустимость этого предположения).

Поток самолетов, заходящих на посадку, - простейший с интенсивностью λ. Если обе

полосы заняты, то самолет ждет в воздухе τ мин, после чего уходит на запасной аэродром.

За каждый отказ в посадке аэропорт платит штраф в S₁ усл. единиц. Строительство

новой посадочной полосы стоит S₂ усл. единиц. За какой срок она окупается?

6. Решить задачу 5 в предположении, что время ожидания посадки в воздухе

распределено экспоненциально со средним значением 1/υ мин. и самолет уходит на запасной аэродром, если кроме него в воздухе уже ждут посадки m самолетов.

7. Грузовые вагоны поступают под разгрузку, образуя простейший поток

интенсивностью λ. Время обработки одного вагона бригадой грузчиков распределено экспоненциально со средним значением 1/υ мин. Что выгоднее: а) интенсифицировать разгрузку вдвое, доведя среднее время до 1/υ ₀ мин. или б) добавить еще одну бригаду грузчиков? Сравнить варианты а) и б):

1) по времени простоя вагонов;

2) по числу простаивающих вагонов;

3) по времени простоя грузчиков;

8. Полагая, что 1ч. простоя вагона стоит S₁ руб., а 1 ч. простоя бригады грузчиков – S₂

руб., дать решение задачи 7 в функции S₁/S₂.

9. n рабочих обслуживают m станков, каждый из которых характеризуется простейшим

потоком неисправностей с интенсивностью λ. Время устранения неисправностей распределено экспоненциально со средним значением 1/υ.

Выбрать критерий эффективности СМО и проанализировать структуру, сравнивая со

случаем, когда за каждым рабочим закреплены два определенных станка.

10. Телефонные вызовы заданного абонента составляют простейший поток с параметром

λ. Длительность каждого разговора распределена экспоненциально с параметром ν. Число неисправностей линии подчинено распределению Пуассона с параметром а. Время устранения неисправности имеет экспоненциальное распределение со средним значением τ.

1) какова вероятность того, что линией нельзя воспользоваться из-за занятости

или неисправности?

2) какова вероятность, что возникшая неисправность оборвет телефонный

разговор?

3) Какова вероятность, что начатый телефонный разговор не прервется поломкой

на линии?

4) Полагая, что стоимость ремонта зависит от его продолжительности (S_p=1/τ), а

доход от каждого обслуженного вызова равен S₀, определить расходы по ремонту линии.

Контрольные вопросы

1. Какие показатели эффективности СМО Вы знаете?

2. Что значит «оптимизировать СМО»?

3. Какие показатели должны быть учтены в обобщенном критерии экономической эффективности (на примере различных типов СМО)?

ЛИТЕРАТУРА

1. Бомас В.В., Булыгин В.С. Элементы теории Марковских процессов и ее технические приложения: Учебное пособие. - М.: МАИ, 1980.

2. Вентцель Е.С. Исследование операций. – М.: Наука, 1989.

3. Дунин – Барковский И.В., Смирнов Н.В. теория вероятностей и математическая статистика. – М.: Гостехтеориздат, 1955.

СОДЕРЖАНИЕ

Предисловие……………………………………………………………………………..3

Работа №1. Исследование нестационарного режима в Марковской системе

массового обслуживания методом имитационного моделирования……………………..4

Работа №2. Исследование систем массового обслуживания методом

имитационного моделирования………………………………………………………........11

Работа №3. Исследование надежности резервированной восстанавливаемой

системы методами теории массового обслуживания….....................................................15

Работа №4. Оптимизация параметров системы массового обслуживания.…...........20

Литература………………………………………………………………………………25