
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные свойства
|
|
Натуральные числа.
Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте. Последовательность всех натуральных чисел, расположенных в порядке их возрастания, называется натуральным рядом.
Существуют два подхода к определению натуральных чисел — это числа, возникающие при:
· подсчёте (нумерации) предметов (первый, второй, третий, …);
· обозначении количества предметов (нет предметов, один предмет, два предмета, …).
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля.
Множество всех натуральных чисел принято обозначать символом N{\displaystyle \mathbb {N} } (от лат. naturalis — естественный). Множество натуральных чисел является бесконечным, так как для любого натурального числа n {\displaystyle n} найдётся натуральное число, большее чем {\displaystyle n}n.
Наличие нуля облегчает формулировку и доказательство многих теорем арифметики натуральных чисел, поэтому при первом подходе вводится полезное понятие расширенного натурального ряда, включающего нуль. Расширенный ряд обозначается {\displaystyle \mathbb {N} _{0}}Nₒ или {\displaystyle \mathbb {Z} _{0}.}Zₒ
Операции над натуральными числами.
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
· Сложение. Слагаемое + Слагаемое = Сумма
· Умножение. Множитель × Множитель = Произведение
· Возведение в степень {\displaystyle a^{b}}bª, где b — основание степени и a — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
· Вычитание. Уменьшаемое − Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
· Деление. Делимое / Делитель = (Частное, Остаток). Частное {\displaystyle p} p и остаток {\displaystyle r}r от деления {\displaystyle a}a на {\displaystyle b}b определяются так: {\displaystyle a=p\cdot b+r}a = p • b + r, причём {\displaystyle 0\leqslant r< b}0 ≤ r < b. Заметим, что именно последнее условие запрещает деление на нуль, так как иначе {\displaystyle a} aa можно представить в виде {\displaystyle a=p\cdot 0+a}a = p•0 + a, то есть можно было бы считать частным {\displaystyle 0}0, а остатком = {\displaystyle a}a.
Основные свойства
1. Коммутативность сложения. {\displaystyle a+b=b+a}a + b = b+a
2. Коммутативность умножения. {\displaystyle ab=ba}ab = ba
3. Ассоциативность сложения. {\displaystyle (a+b)+c=a+(b+c)}(a+b) + c = a + (b+c)
4. Ассоциативность умножения. {\displaystyle (ab)c=a(bc)}(ab)c =a(bc)
5. Дистрибутивность умножения относительно сложения. {\displaystyle {\begin{cases}a(b+c)=ab+ac\\(b+c)a=ba+ca\end{cases}}}a(b+c) = ab + ac
Целые числа.
Целые числа — расширение множества натуральных чисел {\displaystyle \mathbb {N} }N, получаемое добавлением к {\displaystyle \mathbb {N} }N нуля и отрицательных чисел вида {\displaystyle -n} –n. Множество целых чисел обозначается Z{\displaystyle \mathbb {Z}.} Необходимость рассмотрения целых чисел продиктована невозможностью, в общем случае, вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего.
Сумма, разность и произведение двух целых чисел дают снова целые числа, то есть целые числа образуют кольцо относительно операций сложения и умножения.
Z не замкнуто относительно деления двух целых чисел.
Алгебраические свойства
Где a, b, c – целые числа
| сложение | умножение | |
| Замкнутость: | a + b — целое | a × b — целое |
| Ассоциативность: | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| Коммутативность: | a + b = b + a | a × b = b × a |
| существование нейтрального элемента: | a + 0 = a | a × 1 = a |
| существование противоположного элемента: | a + (− a) = 0 | a ≠ ±1 ⇒ 1/ a не является целым |
| Дистрибутивность умножения относительно сложения: | a × (b + c) = (a × b) + (a × c) |
Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b, {\displaystyle b\not =0}b ≠ 0, существует единственный набор целых чисел q и r, что a = bq + r и {\displaystyle 0\leq r< |b|} 0 ≤ r ≤ | b |, где | b | — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.
Геометрический алгоритм Евклида:
Пусть даны два отрезка длины a и b. Вычтем из большего отрезка меньший и заменим больший отрезок полученной разностью. Повторяем эту операцию, пока отрезки не станут равны. Если это произойдёт, то исходные отрезки соизмеримы, и последний полученный отрезок есть их наибольшая общая мера. Если общей меры нет, то процесс бесконечен. В таком виде алгоритм описан Евклидом[2] и реализуется с помощью циркуля и линейки.
Рациональные числа.
Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью {\displaystyle {\frac {m}{n}}}m/n, числитель {\displaystyle m}m —целое число, а знаменатель {\displaystyle n}n — натуральное число.
Множество рациональных чисел обозначается {\displaystyle \mathbb {Q} }Q.
Все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число
Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа {\displaystyle a={\frac {m}{n}}} a=m/n знаменатель {\displaystyle n=1}n = 1, то {\displaystyle a=m} a = m является целым числом.
Основные свойства
1.Упорядоченность. Для любых рациональных чисел {\displaystyle a}a и {\displaystyle b}b существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений: «{\displaystyle < }<», «{\displaystyle > }>» или «{\displaystyle =}=». Это правило называется правилом упорядочения и формулируется следующим образом:
два неотрицательных числа {\displaystyle a={\frac {m_{a}}{n_{a}}}}a = mₐ /nₐ и b= {\displaystyle b={\frac {m_{b}}{n_{b}}}}mₑ /nₑ связаны тем же отношением, что и два целых числа {\displaystyle m_{a}\cdot n_{b}} mₐ • nₑ и {\displaystyle m_{b}\cdot n_{a}} mₑ • nₐ;
два отрицательных числа {\displaystyle a}a и {\displaystyle b} b связаны тем же отношением, что и два неотрицательных числа {\displaystyle \left|b\right|}| a | и {\displaystyle \left|a\right|}| b |;
если же {\displaystyle a}a неотрицательно, а {\displaystyle b}b — отрицательно, то {\displaystyle a> b} a > b.
2. Операция сложения. Для любых рациональных чисел {\displaystyle a}a и {\displaystyle b}b существует так называемое правило суммирования, которое ставит им в соответствие некоторое рациональное число {\displaystyle c}c. При этом само число {\displaystyle c}c называется суммой чисел {\displaystyle a}a и {\displaystyle b}b и обозначается {\displaystyle \left(a+b\right)}(a+b), а процесс отыскания такого числа называется суммированием. Правило суммирования имеет следующий вид:
 +
+  =
= 
3. Операция умножения. Для любых рациональных чисел {\displaystyle a}a и {\displaystyle b}b существует так называемое правило умножения, которое ставит им в соответствие некоторое рациональное число {\displaystyle c}c. При этом само число {\displaystyle c}c называется произведением чисел {\displaystyle a}a и {\displaystyle b}b и обозначается {\displaystyle \left(a\cdot b\right)}(a•b), а процесс отыскания такого числа также называется умножением. Правило умножения имеет следующий вид

 =
= 
4. Транзитивность отношения порядка. Для любой тройки рациональных чисел {\displaystyle a}a, {\displaystyle b}b и {\displaystyle c}c если {\displaystyle a}a меньше {\displaystyle b}b и {\displaystyle b}b меньше {\displaystyle c}c, то {\displaystyle a}a меньше {\displaystyle c}c, а если {\displaystyle a}a равно {\displaystyle b}b и {\displaystyle b}bравно {\displaystyle c}c, то {\displaystyle a}a равно {\displaystyle c}c
5. Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
6.Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
7.Наличие нуля. Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
8.Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.
9.Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
10.Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
11.Наличие единицы. Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
12.Наличие обратных чисел. Любое ненулевое рациональное число имеет обратное рациональное число, умножение на которое даёт 1.
13.Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона: (a+b)*c = a*c + b*c
14.Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число.
15.Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число
16.Аксиома Архимеда. Каково бы ни было рациональное число {\displaystyle a} a, можно взять столько единиц, что их сумма превзойдёт {\displaystyle a}a.

Вычислите значения выражений:
1. 2a – 3a(4-a) +15 при а=-1; а=0, 5
2. k+ 2/3(k-2/3) при к = 1/6
3. (p+0, 6)(p-0, 6) при p = 0, 2
4. 2x + 3y – 5 при x =-1/2; y=-1/3
5. 2  -3
-3  при x =-1; y=2
при x =-1; y=2
6. (2x-  )(x+3) при x = 3
)(x+3) при x = 3
7. (t+3)(t-2)(t+2) при t = -1
8. (x+123)(x+17)  при x = 7
при x = 7
9. (y-32)+(y-  +12) –
+12) – 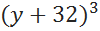 при y =11
при y =11
10. (t +  )(t -
)(t -  ) при t =13
) при t =13
11. (p -  ) + (p +
) + (p +  ) при p = 7
) при p = 7
12.  при x =5
при x =5

Понятие дроби.
Определение 3.
Запись вида  , в которой a и b – числа или выражения, называется дробью. Причем выражение a называется числителем дроби, а выражение b – знаменателем этой дроби.
, в которой a и b – числа или выражения, называется дробью. Причем выражение a называется числителем дроби, а выражение b – знаменателем этой дроби.
Примечания:
1.Если a b – числовые выражения, то  – числовая дробь.
– числовая дробь.
2.Если значение знаменателя дроби равно нулю, то дробь не определена или не имеет значения, или не существует.
Определение 4.
Значение преременной или неизвестного, при которой (котором) выражение обращается в ноль или равно нулю, называется корнем (или нулем) выражения.

Определение 5.
Дробь равна нулю, если числитель ее равен нулю, а знаменатель дроби не равен нулю, т.е.



Упрожнения на умножения многочлена на одночлен или многочлен.
1. (3  b – 5a
b – 5a  )(-
)(-  b)
b)
2. (2  +3a -2)(4a + 1)
+3a -2)(4a + 1)
3. (2x-1)(3x+2) -6x(2x+3) +6 
4. 2ax(a-x) – ( -(
-( (a-3x) -
(a-3x) -  (2ax-a)))
(2ax-a)))
5. (4a+5)(4a-5)
6. (2a -3)(4  +6a+9)
+6a+9)
7. (3a +4)(3a+4)
8. (a+2b)(a+2b)(a+2b)
9. (3-2b)(3-2b)(3-2b)
10. ( –a + 1)(
–a + 1)( +a +1)
+a +1)
11. ( +2x +3)(
+2x +3)( – 2x +3)
– 2x +3)
12. ( +
+  -
-  +
+  )(
)( -
-  +
+  -
-  )(x-z-y+a)
)(x-z-y+a)
13. (13x+17y)( +12y)(12x+
+12y)(12x+  )
)

17.( +b+
+b+  )(a+
)(a+  -17c)
-17c)
18.(x+y-z)(4x+23z-11y)(x+y)
19.( +
+  -
-  +1)(
+1)(
20.( x-
x-  p)(
p)( -1)(p+x)
-1)(p+x)
21.(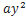 -x)(
-x)(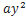 +x-1)
+x-1)
22.( +p)(p-1+
+p)(p-1+  (
( -37xp)
-37xp)
23.(x-z-y+p)( )
)
24.(m+  )(
)( )(x
)(x 
25.(z-x)(z-y)(y-z)(y-x)(x-z)(x-y)
26.(a+2c+5b) 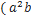 -33bc)
-33bc)
27.(zxy-  (
( +zy)(
+zy)( -zx)
-zx)
28.(x-q+z)( +q)
+q)
29.(y-z-x)( )
)
30.(xz+yx-ax)(z+  -
-  )
)
31.(a  +b
+b  +c
+c  +d)(a
+d)(a  -b
-b  -c
-c  +dx)
+dx)
32.((a  +b
+b  +c
+c  +d)(
+d)( +y-z)+(z+c)(
+y-z)+(z+c)( )(z+x)
)(z+x)

