Функциональная полнота

Как видно из табл.2.1, все функции попарно связаны между собой посредством отрицания, т.е. (і=0, 1, …15). Отсюда следуют зависимости для констант 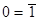и , для функций одной переменной (двойное отрицание) и для функций двух переменных:

х₁х₂=х₁/х₂; х₁< х₂=х₁> х₂ ; х₁Ä х₂=х₁~х₂ ; х₁+х₂=х₁vх₂;

х₁/х₂=х₁х₂; х₁> х₂=х₁< х₂ ; х₁~х₂=х₁Ä х₂; х₁vх₂=х₁+х₂.

Из этих зависимостей следует, что любую функцию двух переменных, включая константы, можно выразить в аналитической форме через совокупность шести функций, содержащей отрицание и любую из каждой пары (у₀, у₁₅), (у₁, у₁₄), (у₂, у₁₃), (у₆, у₉), (у₇, у₈).

Приняв во внимание, что хх=0 и х+х=1, можно сократить комплект элементарных функций до трех: отрицания `х, конъюнкции х₁х₂ и дизъюнкции х₁+х₂. Совокупность этих функций положена в основу булевой алгебры, которая преимущественно используется при математическом моделировании цифровых систем.

Система функций, суперпозицией которых может быть представлена любая функция из некоторого множества логических функций, называется функционально полной. Система функций является минимально полной, если удаление из нее любой функции превращает эту систему в неполную. Необходимое и достаточное условие функциональной полноты состоит в том, что выбранные функции должны в совокупности обладать всеми свойствами, приведенными в табл. 2.2 (звездочкой * отмечены свойства, которыми обладает данная функция).

Таблица 2.2

Функция	Обозна-чение	Свойства
		Несохра-нение 0	Несохра-нение 1	Несамо-двойст-венность	Нелиней-ность	Немоно-тонность
Константа 0 Константа 1 Отрицание Конъюнкция Дизъюнкция Импликация Эквиваленция Отрицание импликации Сумма по модулю 2 Штрих Шеффера Стрелка Пирса	х х1х2 х1+х2 х1> х2 х1~х2 х1< х2   х1Ä х2 х1/х2 х1vх2	* *     * *   * *	*   *     *   * * *	* * * * * * *   * * *	* * *   *     * *	*   * *     * *