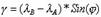Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вывод формулы сближения меридианов.
|
|
На сфере наметим две точки A и B, лежащие на одной параллели, то есть, имеющие одинаковую широту
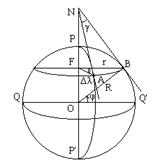 Проведем на поверхности сферы экватор и параллель точек A и B; в плоскости параллели проведем радиусы параллели FA = r и FB = r; угол между ними равен разности долгот точек.
Проведем на поверхности сферы экватор и параллель точек A и B; в плоскости параллели проведем радиусы параллели FA = r и FB = r; угол между ними равен разности долгот точек.
Через точки A и B проведем полуденные линии AN и BN, которые, пересекаясь на продолжении оси вращения Земли, образуют угол γ, являющийся сближением меридианов точек A и B. Требуется выразить Рис.1.13 угол γ через координаты точек A и B, то есть, через широту φ и долготы λ A и λ B, причем Δ λ = λ B - λ A.
Выразим длину дуги AB двумя способами: из Δ ABN AB = BN * γ и из Δ ABF AB = r * Δ λ (углы γ и Δ λ выражены в радианах). Далее пишем: BN*γ =r* Δ λ, откуда 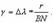 Радиус параллели выразим из Δ OFB r = R*Cos(φ), а отрезок BN - из Δ ONB BN = R * Ctg(φ), где R - радиус сферы; тогда γ = Δ λ * Sin(φ) или
Радиус параллели выразим из Δ OFB r = R*Cos(φ), а отрезок BN - из Δ ONB BN = R * Ctg(φ), где R - радиус сферы; тогда γ = Δ λ * Sin(φ) или