
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисления с использованием арифметики произвольной точности
|
|
MATLAB обычно ведет вычисления с числами, представленными в формате плавающей точки с двойной точностью. Это довольно высокая точность, обеспечивающая потребности практических вычислений в прикладных задачах. Однако ряд задач теории чисел, численного кодирования и некоторых других требует выполнения вычислений вообще без какой - либо погрешности или со сколь угодно малой погрешностью. Такие вычисления не очень удачно называют арифметикой произвольной точности: правильнее говорить о точной арифметике.
Для проведения вычислений в арифметике произвольной точности служит команда vpa:
R=vpa(S) – возвращает результат вычислений символьного выражения S, используя арифметику произвольной точности с текущим числом цифр D, установленным функцией digits. Результат R имеет тип sym;
R=vpa(S, D) – возвращает результат вычислений выражения S с текущим числом цифр D.
Переменная S может быть символьным массивом.
Примеры:
> > vpa(exp(1), 50)
ans =
2.7182818284590455348848081484902650117874145507813
> > vpa([2*pi, exp(1), log(2)], 10)
ans =
[ 6.283185308, 2.718281828,.6931471806]
Команда digits служит для установки числа цифр в числах арифметики произвольной точности. Она используется в одном из следующих вариантов:
digits – возвращает число значащих цифр в числах арифметики произвольной точности (по умолчанию 32);
digits(D) – устанавливает заданное число цифр D для арифметики произвольной точности.
Примеры вычисления числа π с 32 и 6 значащими цифрами:
> > digits
Digits = 32
> > vpa pi
ans =
3.1415926535897932384626433832795
> > digits 6
> > vpa pi
ans =
3.14159
3 КОМАНДЫ УПРОЩЕНИЯ ВЫРАЖЕНИЙ – simplify, simple
Команда simplify(S) упрощает символьное выражение или массив символьных выражений S. Если упрощение невозможно, то возвращается исходное выражение.
Пример для символьного выражения:
> > syms a b x
> > simplify((a^2-2*a*b+b^2)/(a-b))
ans =
a-b
Пример для вектор-столбца символьных выражений:
> > V=[sin(x)^2+cos(x)^2; log(a*b)]
V =
[ cos(x)^2+sin(x)^2]
[ log(a*b)]
> > simplify(V)
ans =
[ 1]
[ log(a*b)]
Возможности проведения упрощений с помощью команды simplify в Symbolic не обладают возможностями системы Maple в полной мере в связи с отсутствием опций, определяющих путь упрощения. Дополнительные возможности упрощения обеспечивает команда simple.
Команда simple(S) выполняет различные алгебраические преобразования символьного выражения S и выводит как промежуточные результаты, так и самый короткий результат. В модификации [R, HOW] = simple(S) промежуточные результаты не выводятся. Результат упрощений содержится в R, а в HOW указывается выполняемое преобразование. Следующие примеры иллюстрируют работу функции:
> > syms x
> > [R, HOW]=simple(cos(x)^2+sin(x)^2)
R =
HOW =
combine
> > [R, HOW]=simple(2*cos(x)^2-sin(x)^2)
R =
3*cos(x)^2-1
HOW =
simplify
> > [R, HOW]=simple(cos(x)^2-sin(x)^2)
R =
cos(2*x)
HOW =
combine
Существует более короткая модификация [R] = simple(S):
> > [R]=simple(cos(x)^2-sin(x)^2)
R =
cos(2*x)
4 КОМАНДА РАСШИРЕНИЯ ВЫРАЖЕНИЙ – expand
Команда expand(S) расширяет символьные выражения массива S. Рациональные выражения она раскладывает на простые дроби, полиномы – на полиномиальные выражения и т. д. Функция работает со многими алгебраическими и тригонометрическими функциями.
Примеры:
> > syms a b x
> > S=[(x+2)*(x+3)*(x-4), sin(2*x)];
> > expand(S)
ans =
[ x^3+x^2-14*x-24, 2*sin(x)*cos(x)]
> > expand(sin(a+b))
ans =
sin(a)*cos(b)+cos(a)*sin(b)
> > expand((a+b)^3)
ans =
a^3+3*a^2*b+3*a*b^2+b^3
5 РАЗЛОЖЕНИЕ ВЫРАЖЕНИЙ НА ПРОСТЫЕ МНОЖИТЕЛИ – КОМАНДА factor
Команда factor(S) поэлементно разлагает символьные выражения массива S на простые множители, а целые числа – на произведение простых чисел.
Примеры:
> > x=sym('x');
> > factor(x^7-1)
ans =
(x-1)*(x^6+x^5+x^4+x^3+x^2+x+1)
> > factor(sym('123456789'))
ans =
(3)^2*(3803)*(3607)
Пусть требуется найти определитель D (команда det) и обратную матрицу A-1 (команда inv) символьной матрицы
A =.
Решение:
> > syms a b
> > A=[a b; a^2 b^2]
A =
[ a, b]
[ a^2, b^2]
> > D=det(A)
D =
a*b^2-b*a^2
> > factor(D)
ans =
-a*b*(-b+a)
> > A1=inv(A)
A1 =
[ -b/a/(-b+a), 1/a/(-b+a)]
[ a/b/(-b+a), -1/b/(-b+a)]
6 ПРИВЕДЕНИЕ ПОДОБНЫХ ЧЛЕНОВ – КОМАНДА collect
Команда collect(S, v) работает с символьными полиномами S нескольких переменных, где v – одна из переменных полинома. Эта функция возвращает разложение полинома S по степеням v (S может быть массивом полиномов).
Примеры:
> > syms x y
> > S=[x^3*y^2+x^2*y+3*x*y^2, x^4*y-y*x^2];
> > collect(S, x)
ans =
[ x^3*y^2+x^2*y+3*x*y^2, x^4*y-x^2*y]
> > collect(S, y)
ans =
[ (x^3+3*x)*y^2+x^2*y, (x^4-x^2)*y]
7 ОБЕСПЕЧЕНИЕ ПОДСТАНОВОК – КОМАНДА subs
Одной из самых эффективных и часто используемых операций символьной математики является операция подстановки. Она реализуется с помощью команды subs со следующими формами записи:
subs(S) заменяет в символьном выражении S все переменные их символьными значениями, которые берутся из вычисляемой функции или рабочей области среды MATLAB;
subs(S, NEW) заменяет все свободные символьные переменные в S из списка NEW;
subs(S, OLD, NEW) заменяет OLD на NEW в символьном выражении S. При одинаковых размерах массивов OLD и NEW замена идет поэлементно. Если S и OLD – скаляры, а NEW – числовой массив или массив ячеек, то скаляры расширяются до массива результатов.
Примеры:
> > syms a b x y;
> > subs(x-y, y, 1)
ans =
x-1
> > subs(sin(x)+cos(y), [x y], [a b])
ans =
sin(a)+cos(b)
Подстановка вместо переменной ее числового значения приводит к вычислению символьной функции от значения аргумента, например:
> > s=sym('x^(x+1)');
> > f=subs(s, 'x', 1.5)
f =
2.7557
Число можно заменить его символьным представлением и затем найти значение функции с произвольной точностью при помощи команды vpa:
> > f=subs(s, 'x', '1.5')
f =
(1.5)^((1.5)+1)
> > vpa(f, 40)
ans =
2.7556759606310753604719445840441
8 ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ – КОМАНДА limit
Для вычисления пределов функции F(x), заданной в аналитическом (символьном) виде, служит команда limit, которая используется в одном из следующих вариантов:
limit(F, x, a) – возвращает предел символьного выражения F в точке x = a;
limit(F, x, a, 'right') или limit(F, x, a, 'left') – возвращает предел в точке a справа или слева.
Продемонстрируем приемы вычисления пределов на следующих примерах:
а); б) с); д);
е); ж).
Решения в указанном порядке имеют вид:
> > syms a x
> > limit(sin(a*x)/(a*x), x, 0)
ans =
> > limit((1+3/x)^(2*x), x, inf)
ans =
exp(6)
> > limit(1/(1-x), x, 1)
ans =
NaN
Здесь переменная NaN означает, что предела функции в точке x = 1 не существует.
> > limit(1/(1-x), x, 1, 'right')
ans =
-inf
Правосторонний предел функции в точке x = 1 существует и равен - ∞.
> > limit(1/(1-x), x, 1, 'left')
ans =
inf
Левосторонний предел функции в точке x=1 существует и равен +∞.
> > limit(x*(log(a+x)-log(x))/5, x, inf)
ans =
1/5*a
9 ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ – КОМАНДА diff
Для вычисления в символьном виде производных от выражения S служит команда diff, записываемая в форме diff(S, x, n). Она возвращает символьное значение n -ой производной (производной степени n) от символьного выражения или массива символьных выражений S по переменной x, т. е.
Sn(x) =.
В формате diff(S, x) находится первая производная (n = 1 по умолчанию).
Пример:
Найти первую и третью производные функции y = x2sinx.
Решение:
> > syms x
> > y=x^2*sin(x);
> > diff(y, x)
ans =
2*x*sin(x)+x^2*cos(x)
> > diff(y, x, 3)
ans =
6*cos(x)-6*x*sin(x)-x^2*cos(x)
Если S массив, то diff возвращает массив, элементами которого являются производные от исходных функций, образующих массив.
Пример:
> > syms a x
> > Y=[a*log(x); x^a]
[ a*log(x)]
[ x^a]
> > diff(Y, x)
ans =
[ a/x]
[ x^a*a/x]
Если выражение S зависит от нескольких переменных, например, S=S(x, y), то ее частная производная (или S'x(x, y)) по аргументу x есть производная этой функции по x при постоянном значении y.
В декартовой системе координат на плоскости xOy градиент функции S(x, y) есть вектор
grad S =.
Частными производными второго порядка функции S=S(x, y) называются частные производные от ее первых производных,, т. е.
=, =, =, =.
Частные производные второго порядка обозначаются также символами S''xx(x, y), S''xy(x, y), S''yx(x, y), S''yy(x, y). Аналогично определяются и обозначаются частные производные более высоких порядков. Смешанные производные второго порядка, отличающиеся только порядком дифференцирования, равны между собой при условии их непрерывности: S''xy(x, y) = S''yx(x, y).
Пример:
Для функции двух переменных f(x, y) = arcsinxy найти gradf(x; y) и вычислить его в точке (0; 0). Проверить выполнение условия f''xy(x, y) = f''yx(x, y).
Решение:
> > syms x y
> > f=asin(x*y);
> > x1=diff(f, x)
x1 =
y/(1-x^2*y^2)^(1/2)
> > pretty(x1)
y
---------------
2 2 1/2
(1 - x y)
Т. е. =.
> > y1=diff(f, y)
y1 =
x/(1-x^2*y^2)^(1/2)
> > pretty(y1)
x
---------------
2 2 1/2
(1 - x y)
Т. е. =. Тогда grad(arcsinxy) =.
Проверка:
> > subs([x1 y1], [x y], [0 0])
ans =
0 0
Итак, grad(arcsinxy) │ (0; 0) = (0; 0).
> > xy=diff(x1, y)
xy =
1/(1-x^2*y^2)^(1/2)+y^2/(1-x^2*y^2)^(3/2)*x^2
> > [m]=simple(xy)
m =
1/(1-x^2*y^2)^(3/2)
> > pretty(m)
---------------
2 2 3/2
(1 - x y)
Следовательно, =.
> > yx=diff(y1, x)
yx =
1/(1-x^2*y^2)^(1/2)+y^2/(1-x^2*y^2)^(3/2)*x^2
> > [m]=simple(yx)
m =
1/(1-x^2*y^2)^(3/2)
> > pretty(m)
---------------
2 2 3/2
(1 - x y)
Значит, =.
Окончательный результат:
grad(arcsinxy) │ (0; 0) = (0; 0) и f''xy(x, y) = f''yx(x, y) =.
10 ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ – КОМАНДА int
В ряде случаев возникает необходимость вычисления неопределенных и определенных интегралов
I = dx и I = dx.
Здесь f(x) – подынтегральная функция независимой переменной x, a нижний и b верхний пределы интегрирования для определенного интеграла.
Команда int(f, x) возвращает неопределенный интеграл (первообразную функцию) от символьного выражения f по переменной x.
Команда int(f, x, a, b) возвращает значение определенного интеграла от символьного выражения f по переменной x с пределами от а до b.
Подынтегральная функция f может зависеть от символьных параметров, а также быть массивом символьных выражений.
Если f массив, то int(f, x) возвращает массив первообразных, а int(f, x, a, b) – массив значений определенных интегралов.
Примеры:
> > syms x
> > f=[sin(x); 1/x]
f =
[ sin(x)]
[ 1/x]
> > int(f, x)
ans =
[ -cos(x)]
[ log(x)]
> > int(f, x, 1, 2)
ans =
[ -cos(2)+cos(1)]
[ log(2)]
Пример:
Вычислить неопределенный интеграл
dx.
Решение:
> > syms x a
> > int(log(x+a)/sqrt(x+a), x)
ans =
2*log(x+a)*(x+a)^(1/2)-4*(x+a)^(1/2)
> > [m]=simple(ans)
m =
2*(x+a)^(1/2)*(log(x+a)-2)
Полученную первообразную 2(ln(x+a) - 2), зависящую от символьного параметра a, проверим дифференцированием по x:
> > diff(m, x)
ans =
1/(x+a)^(1/2)*(log(x+a)-2)+2/(x+a)^(1/2)
> > [m]=simple(ans)
m =
log(x+a)/(x+a)^(1/2)
> > pretty(m)
log(x + a)
-----------
1/2
(x + a)
В результате дифференцирования получена подынтегральная функция
,
т. е. выражение 2(ln(x+a) - 2) действительно является первообразной.
Пример:
Вычислить определенный интеграл
dx.
Решение:
Подынтегральная функция задана в аналитическом виде с символьными переменными a, b, x, а пределами интегрирования являются символьные переменные c, d. Интегрировать можно по любой из переменных a, b, x. Здесь интегрирование осуществляется по переменной x, поэтому int возвращает значение интеграла, выраженное через параметры a, b, c, d
> > syms x a b c d
> > int(x/(a+b*x^2), x, c, d)
ans =
1/2*(log(a+d^2*b)-log(a+c^2*b))/b
> > pretty(ans)
2 2
log(a + d b) - log(a + c b)
1/2 --------------------------------
b
Пример:
Вычислить определенный интеграл по переменной b
db.
Решение:
> > syms x a b c d
> > int(x/(a+b*x^2), b, c, d)
ans =
(log(a+d*x^2)-log(a+c*x^2))/x
> > pretty(ans)
2 2
log(a + d x) - log(a + c x)
--------------------------------
x
От символьных параметров могут зависеть и кратные определенные интегралы.
Пример:
Вычислить тройной интеграл
(x2+y2)zdxdydz.
Решение:
Применив команду int трижды, получим символьный ответ:
> > syms a x y z
> > int(int(int((x^2+y^2)*z, x, 0, a), y, 0, a), z, 0, a)
ans =
1/3*a^6
Команда int не позволяет получить неопределенный интеграл от произвольной функции.
Пример:
Вычислить неопределенный интеграл
dx.
Решение:
При вводе int выдается предупреждение об ошибке и команда возвращается без результата:
> > syms x
> > int(exp(abs(sin(x))), x)
Warning: Explicit integral could not be found.
> In C: \matlab6p5\toolbox\symbolic\@sym\int.m at line 58
ans =
int(exp(abs(sin(x))), x)
Это означает, что либо первообразной не существует либо система MATLAB не смогла ее найти.
В некоторых случаях int возвращает выражение для первообразной через специальные функции.
Пример:
Вычислить неопределенный интеграл
dx.
Решение:
> > syms x
> > int(sin(x)/x)
ans =
sinint(x)
Ответ содержит функцию интегральный синус, которая определяется интегралом с переменным верхним пределом:
Si(x) = dt.
Вычисление несобственных интегралов, зависящих от параметров, имеет некоторые особенности.
Пример:
Вычислить несобственный интеграл
dt.
Решение:
Команда int возвращается без результата:
> > syms a n t
> > int(t^n*exp(-a*t), t, 0, inf)
ans =
int(t^n*exp(-a*t), t = 0.. inf)
Система MATLAB не смогла вычислить интеграл потому, что величина интеграла зависит от знака параметра n, который при определении n остается незаданным. При инициализации символьной переменной n укажем ее знак, например:
> > syms a t
> > n=sym('n', 'positive');
> > int(t^n*exp(-a*t), t, 0, inf)
ans =
1/(a^n)/a*gamma(n)*n
Значение интеграла выражается через гамма - функцию, информацию о которой можно получить с помощью команды doc gamma. Если n целое, то gamma(n)× n = n!, и в таком случае
dt =.
Пример:
Вычислить определенный интеграл
dx.
Решение:
Команда int возвращает символьное значение определенного интеграла, выраженное через функцию арксинус:
> > syms x
> > format long
> > int(asin(x), x, 0, pi/4)
ans =
1/4*pi*asin(1/4*pi)+1/4*(16-pi^2)^(1/2)-1
Для получения решения в естественной форме достаточно активизировать с помощью мыши строку ответа и нажать клавишу < Enter>. Будет получен следующий ответ (в установленном формате вывода):
ans =
0.32847177096777
Команда vpa (см. раздел 2) позволяет вывести на экран результат вычислений с любым числом текущих цифр, например, с 20:
> > int(asin(x), x, 0, pi/4)
ans =
1/4*pi*asin(1/4*pi)+1/4*(16-pi^2)^(1/2)-1
> > vpa(ans, 20)
ans =
.3284717709677653169
Пример:
Вычислить несобственный интеграл
dx.
Решение:
> > syms x
> > int(1/sqrt(abs(x-2)), x, 1, 3)
ans =
Пример:
Вычислить несобственный интеграл
dx.
Решение:
> > syms x
> > int(x*exp(-x), x, 0, inf)
ans =
Ранее система MATLAB не смогла найти первообразную от функции e|sinx|.
Но она позволяет вычислить определенный интеграл от этой функции.
Пример:
Вычислить определенный интеграл
I = dx.
Решение:
При обращении к int выдается предупреждение об ошибке и команда возвращается без результата:
> > syms x
> > I=int(exp(abs(sin(x))), x, 0, 2*pi)
I =
int(exp(abs(sin(x))), x = 0.. 2*pi)
Это означает, что команда int символьное решение не нашла. Воспользуемся теперь командой vpa. При интегрировании с 15 текущими цифрами получим:
> > vpa(I, 15)
ans =
12.4175160714222
Пример:
Вычислить двойной интеграл
I = esin(x² +y²)dxdy.
Решение:
Двойное применение int выдает предупреждение об ошибке и команда возвращается без результата:
> > syms x y
> > I=int(int(exp(sin(x^2+y^2)), x, 0, pi), y, 0, pi)
I =
int(int(exp(sin(x^2+y^2)), x = 0.. pi), y = 0.. pi)
Символьное решение не найдено. Совместное применение int и vpa возвращает приближенное значение интеграла. При вычислениях с 10 текущими цифрами получим:
> > vpa(int(int(exp(sin(x^2+y^2)), x, 0, pi), y, 0, pi), 10)
ans =
13.44629794
Пример:
Вычислить тройной интеграл
I = sin(x2+y2+z2)dxdydz.
Решение:
Тройное обращение к int возвращает символьное решение, выраженное через гипергеометрическую функцию и интегралы Френеля:
> > syms x y z
> > I=int(int(int(sin(x^2+y^2+z^2), x, 0, pi), y, 0, pi), z, 0, pi);
> > [R]=simple(I)
R =
1/18*pi^(5/2)*2^(1/2)*(6*pi^2*hypergeom([3/4], [3/2, 7/4], -1/4*pi^4)*FresnelC(2^(1/2)*pi^(1/2))*hypergeom([1/4], [1/2, 5/4], -1/4*pi^4)-pi^4*hypergeom([3/4], [3/2, 7/4], -1/4*pi^4)^2*FresnelS(2^(1/2)*pi^(1/2))+9*hypergeom([1/4], [1/2, 5/4], -1/4*pi^4)^2*FresnelS(2^(1/2)*pi^(1/2)))
Вычислим интеграл командами int и vpa с 15 текущими цифрами:
> > vpa(int(int(int(sin(x^2+y^2+z^2), x, 0, pi), y, 0, pi), z, 0, pi), 15)
ans =
.280500993612534
11 РАЗЛОЖЕНИЕ В РЯД ТЕЙЛОРА – КОМАНДА taylor
В задачах аппроксимации и приближения функций f(x) важное место занимает их разложение в ряд Тейлора в окрестности точки a:
f(x) =  .
.
Частным случаем этого ряда при a = 0 является ряд Маклорена:
f(x) =  .
.
Для получения разложения аналитической функции f в ряд Тейлора (и Маклорена) служит команда taylor:
taylor(f) – возвращает разложение в ряд Маклорена до шестой степени. В общем случае, когда необходимо получить разложение в ряд Тейлора до n - й степени в точке a, относительно которой находится разложение, используется команда taylor(f, n, x, a).
Примеры разложения в ряды Тейлора и Маклорена функции cos(x):
> > syms x
> > taylor(cos(x))
ans =
1-1/2*x^2+1/24*x^4
> > taylor(cos(x), 5, x, 2)
ans =
cos(2)-sin(2)*(x-2)-1/2*cos(2)*(x-2)^2+1/6*sin(2)*(x-2)^3+1/24*cos(2)*(x-2)^4
Пример:
Получить разложение в степенной ряд по степеням x «функции ошибок»
Erf(x) = dt,
которая не выражается в конечном виде через элементарные функции.
Решение:
> > syms x t
> > Pi=sym('pi');
> > taylor(2/sqrt(Pi)*int(exp(-t^2), t, 0, x))
ans =
2/pi^(1/2)*x-2/3/pi^(1/2)*x^3+1/5/pi^(1/2)*x^5
> > [m]=simple(ans)
m =
1/15*x*(30-10*x^2+3*x^4)/pi^(1/2)
> > pretty(m)
2 4
x (30 - 10 x + 3 x)
1/15 -------------------------
1/2
pi
Команда taylortool приводит к появлению окна приложения, изображенного на рисунке 1.

Рисунок 1
Пользователь может вводить формулы различных функций в строке f(x) = и исследовать приближение функции на произвольном интервале отрезком ряда Тейлора, содержащим различное число членов разложения.
12 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ – КОМАНДА solve
Для решения систем уравнений и одиночных уравнений служит команда
solve(expr1, expr2,..., exprN, var1, var2,..., varN). Она возвращает значения переменных varI, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается, что exprI = 0.
Результат может быть возвращен в следующих формах:
для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;
при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде.
Команда solve позволяет найти не только вещественные, но и комплексные решения систем уравнений и одиночных уравнений. Справку по этой команде можно получить, введя команду doc solve.
Пример:
Решить уравнение x3 - 1 = 0.
Решение:
> > syms x, y=x^3-1; S=solve(y)
S =
[ 1]
[ -1/2+1/2*i*3^(1/2)]
[ -1/2-1/2*i*3^(1/2)]
В результате получены три разных значения корня x1 = 1, x2 =, x3 =, которые хранятся соответственно в элементах S(1), S(2), S(3) массива S.
Проверка:
С помощью subs (раздел 7) подставим найденные значения корней в выражение x3 - 1:
> > subs(y, x, S)
ans =
[ 0]
[ (-1/2+1/2*i*3^(1/2))^3-1]
[ (-1/2-1/2*i*3^(1/2))^3-1]
> > [m]=simple(ans)
m =
[ 0]
[ 0]
[ 0]
Выражение x3 - 1 принимает значение 0 при подстановке любого из найденных корней, поэтому x1, x2, x3 являются точными корнями уравнения x3 - 1 = 0.
В общем случае полиномиальное уравнение степени выше 4 не может иметь точного решения, выраженного с помощью радикалов.
Команда solve позволяет решать уравнения, представленные в аналитическом виде.
Пример:
Решить квадратное уравнение ax2+bx+c = 0.
Решение:
> > S=solve('a*x^2+b*x+c=0', x)
S =
[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]
[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]
Команда solve возвратила известные выражения корней x1, 2 = квадратного уравнения ax2+bx+c = 0. Точно также можно выразить с помощью радикалов решения кубического уравнения ax3+bx2+cx+d = 0, хотя эти выражения достаточно сложные.
Пример:
Решить трансцендентное уравнение xlnx+1 - 1 = 0.
Решение:
> > syms x
> > S=solve('x^(log(x)+1)-1', x)
S =
[ exp(0)]
[ exp(-1)]
Проверка:
> > subs(x^(log(x)+1)-1, x, S)
ans =
[ 0]
[ 0]
В данном случае solve нашла точные значения корней x1 = 1, x2 = e− 1.
Пример:
Решить трансцендентное уравнение lnx + 3 - x = 0.
Решение:
> > solve('log(x)+3-x=0')
ans =
[ -lambertw(-exp(-3))]
[ -lambertw(-1, -exp(-3))]
Команда solve возвратила значения корней, выраженные через функцию Ламберта.
Команда vpa возвращает приближенные значения этих корней, вычисленные с 20 значащими цифрами:
> > vpa(ans, 20)
ans =
[.52469097457714872410e-1]
[ 4.5052414957928833670]
Решение любого трансцендентного уравнения достаточно сложная и серьезная проблема. Иногда solve возвращает неверные решения.
Пример:
Решить трансцендентное уравнение sinxlnsinx+xx - 2 = 0.
Решение:
> > syms x
Y=sin(x)^log(sin(x))+x^x-2;
> > S=solve(Y)
S =
1/2*pi
Проверка:
> > subs(Y, S)
ans =
-1+(1/2*pi)^(1/2*pi)
> > vpa(ans, 5)
ans =
1.0327
Найденное решение неверное, т. к. оно не прошло проверку подстановкой.
Команда solve может возвратить не все решения.
Пример:
Решить трансцендентное уравнение sinx+lnx+ex - 1 = 0.
Решение:
> > syms x
> > Y=sin(x)+log(x)+exp(x)-1;
> > S=solve(Y);
> > vpa(S, 5)
ans =
-3.0553-1.7145*i
> > subs(Y, S)
ans =
-.8e-31-.1e-30*i
Возвратив приближенный комплексный корень уравнения x1 = -3, 0553 - 1, 7145i, solve не нашла вещественный корень. С помощью команды ezplot (см. раздел 15) графически определяем, что он находится вблизи значения 0, 4 (рисунок 2):
> > ezplot('sin(x)+log(x)+exp(x)-1', [0, 1, -1, 3])
> > grid

Рисунок 2
Вещественный корень x2=0, 4072 найден в [2] (раздел 6.2) с помощью команды fzero.
Перейдем теперь к системам уравнений.
Пример:
Решить систему уравнений

Решение:
Результатом выполнения команды solve является структура S с полями x и y, каждое из которых содержит символьное представление решения:
> > syms x y
> > Y1=x+y-3;
> > Y2=x*y^2-4;
> > S=solve(Y1, Y2, x, y)
S =
x: [3x1 sym]
y: [3x1 sym]
Выведем в командное окно содержимое структуры:
disp([S.x S.y])
[ 4, -1]
[ 1, 2]
[ 1, 2]
Получили три решения (x1; y1) = (4; -1) и (x2; y2) = (1; 2) (второе – кратности 2), причем (x1; y1) хранится в [ S.x(1) S.y(1) ], а (x2; y2) – в [ S.x(2) S.y(2) ]:
> > disp([S.x(1) S.y(1)])
[ 4, -1]
> > disp([S.x(2) S.y(2)])
[ 1, 2]
Для проверки подставим в выражения Y1 = x+y - 3 и Y2 = xy2 - 4 вначале первое решение, а затем второе:
> > disp(subs([Y1 Y2], [x y], [S.x(1) S.y(1)])
[ 0, 0]
> > disp(subs([Y1 Y2], [x y], [S.x(2) S.y(2)])
[ 0, 0]
Как видим, найдены точные решения, т. к. выражения Y1 и Y2 при их подстановке обратились в 0.
Команда solve допускает использование символьных переменных в качестве выходных аргументов. Эквивалентное обращение к solve в предыдущем примере имеет вид:
> > [x, y]=solve(Y1, Y2, x, y)
x =
[ 4]
[ 1]
[ 1]
y =
[ -1]
[ 2]
[ 2]
Команда solve позволяет решать системы уравнений, заданные в аналитическом виде.
Пример:
Решить систему уравнений относительно x, y, z

Решение:
> > syms a b c x y z
> > Y1=(a+b)/(x+y)+(b+c)/(y+z)-(c+a)/(z+x)-1;
> > Y2=(a+b)/(x+y)-(b+c)/(y+z)+(c+a)/(z+x)-1;
> > Y3=-(a+b)/(x+y)+(b+c)/(y+z)+(c+a)/(z+x)-1;
> > S=solve(Y1, Y2, Y3, x, y, z)
S =
x: [1x1 sym]
y: [1x1 sym]
z: [1x1 sym]
> > disp([S.x S.y S.z])
[ a, b, c]
Проверим найденное решение (a; b; c) подстановкой в систему:
> > subs([Y1 Y2 Y3], [x y z], [S.x S.y S.z])
ans =
[ 0, 0, (-a-b)/(a+b)+1]
> > disp(simplify(ans))
[ 0, 0, 0]
Убеждаемся, что решение найдено верно.
Иногда системе MATLAB можно помочь, преобразовав уравнение или систему уравнений к эквивалентному виду.
Например, уравнение ln(4 - 2x)+x2 - 2 = 0 имеет эквивалентный вид e2− x² +2x - 4 = 0. Можно проверить, что для каждого из этих уравнений команда solve возвращает свой вещественный корень. Это будут разные корни, но каждый из них удовлетворяет исходному уравнению. Существует и третий вещественный корень, который можно найти с помощью команды fzero [2].
Пример:
Решить систему трансцендентных уравнений

Решение:
> > syms x y
> > Y1=3^y*9^x-81;
> > Y2=log10((y+x)^2)-log10(x)-2*log10(3);
> > S=solve(Y1, Y2, x, y)
S =
x: [4x1 sym]
y: [4x1 sym]S =
> > R=[S.x S.y];
> > disp(vpa(R, 10))
[ 16.00000002, -28.00000004]
[ 16.00000002, -3.999999992]
[ 1.000000000, -3.999999996]
[ 1.000000000, 1.999999996]
Получили 4 приближенных решения c 10 значащими цифрами. Однако системе удовлетворяют только первое и последнее из них. Убедимся в этом подстановкой:
> > disp(vpa(subs([Y1, Y2], [x y], [S.x(1) S.y(1)]), 15))
[.1e-12,.15e-13]
> > disp(vpa(subs([Y1, Y2], [x y], [S.x(2) S.y(2)]), 15))
[ 22876792454891.6,.25e-13]
> > disp(vpa(subs([Y1, Y2], [x y], [S.x(3) S.y(3)]), 15))
[ -80.8888888888889,.31e-13]
> > disp(vpa(subs([Y1, Y2], [x y], [S.x(4) S.y(4)]), 15))
[ -.71e-11,.18e-13]
Приближенное равенство [ Y1, Y2 ] » [ 0, 0 ] выполняется только при подстановке в систему первого и последнего решений. В остальных случаях [ Y1, Y2 ] ≠ [ 0, 0 ].
Алгебраическими преобразованиями приведем исходную систему к эквивалентной системе
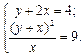
Решим ее:
> > syms x y
> > S=solve('y+2*x=4', '(y+x)^2/x=9', x, y);
> > [S.x S.y]
ans =
[ 1, 2]
[ 16, -28]
Получили два точных решения, являющихся также решениями исходной системы.
Пример:
Решить cистему уравнений

Решение:
> > syms x y z
> > Y1=x+x^2-2*y*z-.1;
> > Y2=y-y^2+3*x*z+.2;
> > Y3=z+z^2+2*x*y-.3;
> > S=solve(Y1, Y2, Y3, x, y, z);
> > R=[S.x S.y S.z];
> > disp(vpa(R, 6))
[ -.541941+.626019e-1*i, -.179057-.433417*i,.148543-.344892*i]
[ -.541941-.626019e-1*i, -.179057+.433417*i,.148543+.344892*i]
[.128241e-1, -.177801,.244688]
[ -1.08804, -.130325,.161425e-1]
[.578802e-1,.156279e-1, -1.24040]
[.374678+.356411*i,.353227-.580416*i, -.281751+.419593*i]
[.374678-.356411*i,.353227+.580416*i, -.281751-.419593*i]
[.121093, 1.17493,.152166e-1]
Получено 8 приближенных решений с 6 значащими цифрами, 4 из которых вещественные (c 3 - го по 5 - е и 8 - е). Проверим все 8 решений подстановкой с помощью цикла for [2]:
> > for i=1: 8
T=subs([Y1 Y2 Y3], [x y z], [S.x(i) S.y(i) S.z(i)]);
disp(vpa(T, 6))
end
[ -.5e-31-.1471e-30*i, -.32e-30+.71e-30*i,.25e-30+.103e-29*i]
[ -.5e-31+.1471e-30*i, -.32e-30-.71e-30*i,.25e-30-.103e-29*i]
[.12e-30,.9e-31, -.13e-30]
[.8e-31,.14e-30, -.3e-31]
[.2e-31, -.6e-31, -.14e-30]
[.637e-29+.829e-29*i, -.754e-29+.15e-30*i,.709e-29-.346e-29*i]
[.637e-29-.829e-29*i, -.754e-29-.15e-30*i,.709e-29+.346e-29*i]
[.17422e-27, -.1012e-28,.12735e-27]
При подстановке любого из решений [ Y1 Y2 Y3 ] » [ 0 0 0 ]. Значит, каждое из них удовлетворяет системе уравнений.
13 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ – КОМАНДА dsolve
Для решения обыкновенных дифференциальных уравнений (систем уравнений) MATLAB имеет команду
r = dsolve('eq1', 'eq2',..., 'cond1', 'cond2',..., 'v').
Она возвращает аналитическое решение дифференциальных уравнений eq1, eq2,..., использующих v как независимую переменную, с граничными и (или) начальными условиями cond1, cond2,.... По умолчанию независимой переменной считается переменная t, обычно обозначающая время. Если в выражениях eqI (condI) не используется знак равенства, то полагается, что eqI (condI) = 0.
Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d2/dt2 и т. д. Имя независимой переменной не должно начинаться с буквы D.
Начальные условия задаются в виде равенств 'y(a) = b' или 'Dy(a) = b', где у – зависимая переменная, a и b – константы, которые могут быть и символьными. Могут быть символьными и константы в уравнениях. Если число начальных условий меньше порядка уравнения, то в решении будут присутствовать произвольные постоянные C1, C2 и т. д. Формы вывода результата такие же, как и для команды solve. Справку по dsolve можно получить, введя команду doc dsolve.
Пример:
Решить дифференциальные уравнения
1) x'' = -2x', 2) y'' = -ax+y', y(0) = b, 3) y(4) - y = 5exsinx+x4, 4) y''+4y'+3y = cost, y(0) = 1, y'(0) = 0.
Решения 3 - го и 4 - го уравнений проверить подстановкой.
Решение:
> > dsolve('D2x=-2*x')
ans =
C1*cos(2^(1/2)*t)+C2*sin(2^(1/2)*t)
> > dsolve('D2y=-a*x+y', 'y(0)=b', 'x')
ans =
a*x+C1*sinh(x)+b*cosh(x)
> > syms x
> > S=dsolve('D4y-y-5*exp(x)*sin(x)-x^4', 'x');
> > [R]=simple(S)
R =
-24-x^4-exp(x)*sin(x)+C1*exp(x)+C2*sin(x)+C3*cos(x)+C4*exp(-x)
Проверка 3-го решения:
> > diff(R, x, 4)-R-5*exp(x)*sin(x)-x^4
ans =
> > S=dsolve('D2y+4*Dy+3*y=cos(t)', 'y(0)=1', 'Dy(0)=0', 't')
S =
1/10*cos(t)+1/5*sin(t)-7/20*exp(-3*t)+5/4*exp(-t)
Проверка 4-го решения:
> > syms t
> > diff(S, t, 2)+4*diff(S, t)+3*S
ans =
cos(t)
Проверка выполнения начальных условий 4 - го решения:
> > subs(S, t, 0)
ans =
> > subs(diff(S, t), t, 0)
ans =
Пример:
Решить систему линейных дифференциальных уравнений

Решение:
> > S=dsolve('Dx = y', 'Dy = -x')
S =
x: [1x1 sym]
y: [1x1 sym]
> > disp([S.x, S.y ])
[ cos(t)*C1+sin(t)*C2, -sin(t)*C1+cos(t)*C2]
Пример:
Решить систему линейных дифференциальных уравнений с начальными условиями и проверить решение


Решение:
> > S=dsolve('Dx = y', 'Dy = -x', 'x(0)=1', 'y(0)=2')
S =
x: [1x1 sym]
y: [1x1 sym]
> > disp([S.x S.y])
[ cos(t)+2*sin(t), -sin(t)+2*cos(t)]
Получено решение: x = cost+2sint, y = -sint+2cost.
Проверка решения:
syms t
> > diff(S.x, t)-S.y
ans =
> > diff(S.y, t)+S.x
ans =
Проверка выполнения начальных условий:
> > subs(S.x, t, 0)
ans =
> > subs(S.y, t, 0)
ans =
Команда dsolve не позволяет получить аналитическое решение дифференциального уравнения произвольного вида.
Пример:
Найти аналитическое решение уравнения Ван-дер-Поля
y'' - (1 - y2)y'+y = 0, y(0) = 2, y'(0) = 0.
Решение:
Обращение к dsolve выдает сообщение о том, что решение не найдено:
> > dsolve('D2y-(1-y^2)*Dy+y=0', 'y(0)=2', 'Dy(0)=0')
ans =
[ empty sym ]
В некоторых случаях dsolve возвращает решение, выраженное через специальные функции.
Пример:
Найти аналитическое решение уравнения Бесселя
x2y''+xy'+(x2 - v2)y = 0.
Решение:
> > dsolve('x^2*D2y+x*Dy+(x^2-v^2)*y=0', 'x')
ans =
C1*besselj(v, x)+C2*bessely(v, x)
Решение выражается через функции Бесселя. Информацию о функциях Бесселя можно получить с помощью команды doc besselj.
14 ПРЯМОЕ И ОБРАТНОЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА – КОМАНДЫ laplace, ilaplace
Преобразование Лапласа любой комплексной функции f(t) действительной переменной t имеет вид
L(s) = f(t)e-stdt.
Функцию f(t) принятоназывать оригиналом, а функцию L(s) – изображением. Функция f(t) должна удовлетворять следующим условиям:
а) f(t) является непрерывной функцией для всех значений t, принадлежащих области определения. (Допускается наличие разрывов первого рода в конечном числе точек, расположенных на интервалах конечной длины. Количество таких интервалов должно быть конечным числом);
б) f(t) = 0 при t < 0;
в) существуют числа M > 0 и p ≥ 0 такие, что для всех t │ f(t) │ < Mept (p называется показателем роста │ f(t) │).
Некоторые простейшие преобразования Лапласа приведены в таблице 7.1.
Таблица 1 − Некоторые преобразования Лапласа
| f(t) | L(s) = f(t)e-stdt. |
| 1 | s-1 |
| e-at | (s+a)-1 |
| sinat | a(s2+a2)-1 |
| tn | n! s-n-1 |
| e-atcoswt | |
| tne-at |
В MATLAB преобразование Лапласа функции f(t) осуществляется с помощью команды laplace(F, t, s).
Найдем с помощью этой команды изображения заданных в таблице 1 оригиналов f(t):
> > syms a t w s
> > n=sym('n', 'positive');
> > laplace(1, t, s)
ans =
1/s
> > laplace(exp(-a*t), t, s)
ans =
1/(s+a)
> > laplace(sin(a*t), t, s)
ans =
a/(s^2+a^2)
> > laplace(t^n, t, s)
ans =
s^(-n-1)*gamma(n+1)
> > laplace(exp(-a*t)*cos(w*t), t, s)
ans =
(s+a)/((s+a)^2+w^2)
> > laplace(t^n*exp(-a*t), t, s)
ans =
gamma(n+1)*(s+a)^(-n-1)
Полученные изображения совпадают с табличными, если учесть, что
gamma(n+1) = n! для целых n (см. раздел 10).
Пример:
Найти изображение функции f(t) = e-2tsin2tcos3t.
Решение:
> > syms t s
> > laplace(exp(-2*t)*sin(2*t)*cos(3*t), t, s)
ans =
5/2/((s+2)^2+25)-1/2/((s+2)^2+1)
> > pretty(ans)
1 1
5/2 ------------- - 1/2 ------------
2 2
(s + 2) + 25 (s + 2) + 1
> > factor(ans)
ans =
2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5)
> > pretty(ans)
s + 4 s - 1
2 ------------------------------
2 2
(s + 4 s + 29) (s + 4 s + 5)
Итак,
L(s) = 2.
Пример:
Найти изображение функции f(t) =.
Решение:
При обращении к laplace команда возвращается без результата:
> > laplace(1/t, t, s)
ans =
laplace(1/t, t, s)
Это означает что либо изображения не существует, либо системе MATLAB не удалось его найти.
Существуют различные модификации laplace (справку можно получить с помощью команды doc laplace).
Обратное преобразование Лапласа имеет вид
f(t) = L(s)estds.
В среде MATLAB обратное преобразование Лапласа функции L(s) можно получить с помощью команды ilaplace(L, s, t). Найдем с ее помощью оригиналы заданных в таблице 1 изображений L(s):
> > syms a t w s
> > n=sym('n', 'positive');
> > ilaplace(1/s, s, t)
ans =
> > ilaplace(1/(s+a), s, t)
ans =
exp(-a*t)
> > ilaplace(a/(s^2+a^2), s, t)
ans =
a/(a^2)^(1/2)*sin((a^2)^(1/2)*t)
> > ilaplace(s^(-n-1)*gamma(n+1), s, t)
ans =
t^n
> > ilaplace((s+a)/((s+a)^2+w^2), s, t)
ans =
exp(-a*t)*cos(w*t)
> > ilaplace(gamma(n+1)*(s+a)^(-n-1), s, t)
ans =
exp(-a*t)*t^n
Полученные оригиналы совпадают с табличными.
Пример:
Найти оригинал полученного ранее изображения
2
функции f(t) = e-2tsin2tcos3t.
Решение:
> > syms t s
> > ilaplace(2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5), s, t)
ans =
1/2*exp(-2*t)*sin(5*t)-1/2*exp(-2*t)*sin(t)
> > factor(ans)
ans =
1/2*exp(-2*t)*(sin(5*t)-sin(t))
Поскольку (sin5t - sint) = sin2tcos3t, то оригинал найден верно.
Пример:
Найти оригинал изображения
L(s) =.
Решение:
Команда ilaplace возвращает решение, выраженное через функцию Хевисайда:
> > syms t s a
> > ilaplace(exp(-2*s)/(s+a), s, t)
ans =
Heaviside(t-2)*exp(-a*(t-2))
Функция Хевисайда (единичная функция) определяется следующим образом:
δ 0(t) = 
Следовательно, найденный оригинал имеет вид
f(t) = 
Пример:
Найти оригинал изображения
L(s) =.
Решение:
Команда ilaplace возвращает решение, выраженное через корни уравнения z4+1 = 0:
> > syms t s
> > ilaplace((s^4-1)/(s^5+s), s, t)
ans =
-1+2*sum(1/4*exp(_alpha*t), _alpha = RootOf(_Z^4+1))
Команда vpa вычисляет приближенное значение оригинала с заданным количеством текущих цифр:
> > vpa(ans, 4)
ans =
-1.+1.000*exp(-.7071*t)*cos(.7071*t)+1.000*exp(.7071*t)*cos(.7071*t)
Пример:
Найти оригинал изображения
L(s) =.
Решение:
Команда ilaplace возвращается без результата:
> > syms t s
> > ilaplace(exp(2*s)/(s+3)^2, s, t)
ans =
ilaplace(exp(2*s)/(s+3)^2, s, t)
Это означает что либо оригинала не существует, либо системе MATLAB не удалось его найти.
Существуют и другие модификации ilaplace (справку можно получить, введя команду doc ilaplace).
15 ГРАФИКИ СИМВОЛЬНЫХ ФУНКЦИЙ – КОМАНДЫ ezplot, ezpolar
Чтобы избавить пользователя от хлопот, связанных с построением графиков функций с помощью стандартных средств (например, команды plot, [2]), в пакет Symbolic введены довольно удобные графические команды класса ezplot:
ezplot(f) – строит график символьно заданной функции f(x) независимой переменной x в интервале[- 2*pi; 2*pi ];
ezplot(f, xmin, xmax) – делает то же, но позволяет задать диапазон изменения независимой переменной x в интервале от xmin до xmax;
ezplot(f, [xmin, xmax, ymin, ymax]) – строит график функции f(x, у) = 0 для xmin < х < xmax, ymin < y < ymax.
Построим график функции sin(t)/t (рисунок 3):
> > ezplot('sin(t)/t'), grid

Рисунок 3
Следующая команда строит график гиперболы u2 - v2 - 1 = 0 для - 3 < u < 3, - 3 < v < 3 (рисунок 4):
> > ezplot('u^2-v^2-1', [-3, 3, -3, 3]), grid

Рисунок 4
Ранее с помощью команды ezplot был построен график на рисунке 2.
График функции f(t) в полярной системе координат строит команда ezpolar:
ezpolar(f) – строит график функции f(t) при изменении угла t от 0 до 2π;
ezpolar(f, [a b]) – строит график функции f(t) при изменении угла t от a до b.
Построим график функции cos3t в полярной системе координат (рисунок 5):
> > ezpolar('cos(3*t)')

Рисунок 5
Помимо команд ezplot и ezpolar, пакет Symbolic поддерживает построение графиков других типов. Так, команда ezcontour служит для построения контурных графиков функций вида f(x, y). Похожая команда ezcontourf строит контурные графики с функциональной окраской областей между линиями равного уровня. Для построения трехмерных графиков параметрически заданных функций служит команда ezplot3. Команды ezsurf, ezsurfc, ezmesh, ezmeshc применяются для построения графиков поверхностей, заданных функциями двух переменных f(x, y). Справку с примерами по применению любой из этих команд можно получить с помощью команды doc < имя команды >.
16 ПРЯМОЙ ДОСТУП К ЯДРУ СИСТЕМЫ Maple – КОМАНДА maple
Применение возможностей системы Maple совместно с возможностями системы MATLAB придает последней особую гибкость и резко расширяет возможности решения сложных математических задач, где целесообразно объединять аналитические (символьные) методы с численными расчетами.
Доступ к большинству функций и команд системы Maple, ядро которой включено в МАТLAB, осуществляется командой maple.
Пример:
Найти аналитическое решение дифференциального уравнения y''+2xy'+ny = 0.
Решение:
Обращение к dsolve приводит к решению, выраженному через функции Уиттекера:
> > dsolve('D2y+2*x*Dy+n*y=0', 'x')
ans =
C1/x^(1/2)*WhittakerW(1/4*n-1/4, 1/4, x^2)*exp(-1/2*x^2)+C2/x^(1/2)*WhittakerM(1/4*n-1/4, 1/4, x^2)*exp(-1/2*x^2)
Непосредственно из МАТLAB функции WhittakerW и WhittakerM недоступны, т.к. их нет в списке mfunlist функций системы Maple, доступных из МАТLAB [2].
Определение функций функций Уиттекера, варианты вызова и подробное описание с примерами использования возвращает команда mhelp Whittaker. Вычислим значение одной из них:
> > maple('WhittakerM(1, 2, 3)')
ans =
WhittakerM(1, 2, 3)
> > vpa(ans, 7)
ans =
10.17605
Ниже приводятся примеры решения в МАТLAB некоторых математических задач с привлечением возможностей системы Maple.