Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция на тонкой пластине.
|
|
|
|
|
Пусть на прозрачную плоскопараллельную тонкую пластинку толщиной d с показателем преломления n (у окружающей среды показатель преломления равен единице) падает параллельный пучок монохроматического света (монохроматическая волна – это строго синусоидальная волна с постоянной во времени частотой и амплитудой). Луч (под лучом будем понимать световые волны, распространяющиеся в определенном направлении) падает на пластину под углом ψ 1 (рис. 1), частично отражается, а частично преломляется. В результате происходит деление амплитуды падающей волны. При отражении от границы среды, оптически более плотной, в среду, менее плотную (отражение в точке О), световая волна меняет фазу своего колебания на противоположную. Изменение фазы на π соответствует «пробегу» волной дополнительного расстояния λ /2 (как говорят, свет при отражении «теряет половину длины волны»). Таким образом, добавив (или вычтя) половину длины волны (в вакууме) к разности хода лучей 1 и 2, мы учтем изменение фазы колебания луча 1 при отражении в точке О.
Лучи 1 и 2 когерентны, так как исходят от одного источника. Разность хода лучей 1 и 2 в точках А и В равна
Δ = nS 2 – S 1,
где S 1 = | OA |, S 2 = | OC | + | CB |, а n – показатель преломления пластины.
Из рис. 1 следует, что S 1 = 2 d · tg(ψ 2)sin(ψ 1), S 2 = 2 d / cos(ψ 2). Далее, воспользовавшись соотношением cos2(ψ 2) = 1 – sin2 (ψ 2) и законом преломления света sin(ψ 2) = sin(ψ 1) / n, получаем
.
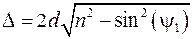С учетом изменения фазы на π окончательно имеем:
. (3)
Если на пути лучей 1 и 2 поставить собирающую линзу, то лучи сойдутся в фокальной плоскости линзы и будут интерферировать. При Δ = k λ (k = 1, 2, 3…) разность фаз, согласно (2), ∆ φ = 2 k π, т. е. колебания придут в точку наблюдения «в фазе» и усилят друг друга, в результате чего получаются максимумы интенсивности; а при Δ = (k + ½)λ (k = 0, 1, 2, 3…) разность фаз ∆ φ = (2 k + 1)π, т. е. колебания придут «в противофазе» и ослабят друг друга, в результате чего получаютсяминимумы интенсивности.
При постоянном угле падения ψ 1 и показателе преломления n результат интерференции зависит только от толщины пластинки d. Поэтому на пластинке переменной толщины возникает система интерференционных полос, каждая из которых соответствует определенному значению толщины пластинки. Картина интерференции в этом случае называется полосами равной толщины. В настоящей работе исследуется интерференционная картина полос равной толщины, называемая кольцами Ньютона.