Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие сведения из теории пределов функции
|
|
Число А называют пределом функции f (x) при 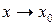 (и пишут
(и пишут  ), если для любого
), если для любого  найдется число
найдется число  зависящее от e, такое, что для всех
зависящее от e, такое, что для всех  , удовлетворяющих условию
, удовлетворяющих условию 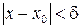 , выполняется неравенство
, выполняется неравенство 
Функция a(x) называется бесконечно малой (б.м.ф.) при 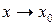 (
( если
если 
Функция f (x) называется бесконечно большой (б.б.ф.) при 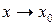 , (
, ( если для любого M > 0 найдётся число
если для любого M > 0 найдётся число  зависящее от М, такое, что для всех
зависящее от М, такое, что для всех  , удовлетворяющих условию
, удовлетворяющих условию 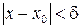 , будет верно неравенство
, будет верно неравенство 
Если функция a(x) есть бесконечно малая при 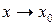 (или
(или  то функция
то функция  является бесконечно большой, и обратно, если функция f (x) бесконечно большая функция при
является бесконечно большой, и обратно, если функция f (x) бесконечно большая функция при 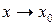 , то
, то  является бесконечно малой функцией.
является бесконечно малой функцией.
Если функции  и
и  бесконечно малые при
бесконечно малые при 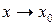 (
( ),
),
то чтобы сравнить их, нужно вычислить предел их отношения. Пусть  Тогда:
Тогда:
— при 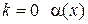 называется бесконечно малой более высокого порядка малости, чем
называется бесконечно малой более высокого порядка малости, чем  ;
;
— при 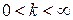
 и
и  одного порядка малости;
одного порядка малости;
— при 
 более низкого порядка малости, чем
более низкого порядка малости, чем  .
.
Если 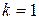 , то бесконечно малые
, то бесконечно малые  и
и  называются эквивалентными:
называются эквивалентными: 
Предел отношения двух бесконечно малых функций не изменится, если каждую бесконечно малую функцию заменить на эквивалентную.
Примеры эквивалентных бесконечно малых функций при
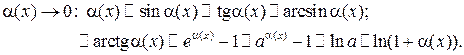
Теоремы о пределах:
1. 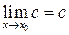 (c =const).
(c =const).
2. Если 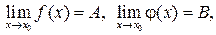 то:
то:
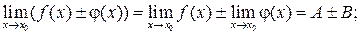


Первый замечательный предел: 
Второй замечательный предел (число е = 2, 718…):
 или
или 
Чтобы найти предел элементарной функции 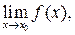 нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если  то, учитывая свойства б.б. и б.м. функций, получим:
то, учитывая свойства б.б. и б.м. функций, получим:
 если
если 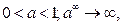 если a > 1.
если a > 1.
Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:
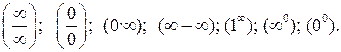
Устранить неопределенность можно с помощью алгебраических преобразований или используя правило Лопиталя.
Правило Лопиталя. Предел отношения двух б.м.  или б.б.
или б.б. 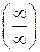 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность  или
или 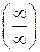 и затем использовать формулу (5).
и затем использовать формулу (5).
Задание 7. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
а) 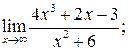 б)
б)  в)
в) 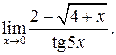
Решение.
а) Подставляя в функцию вместо х предельное значение  , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
 т. к.
т. к. 
Аналогично: 
Имеем неопределенность вида 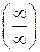 . Используем правило Лопиталя:
. Используем правило Лопиталя:

б) 

в) 
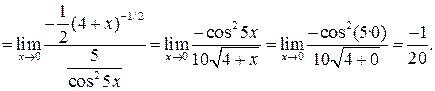
Замечание. Если, применив правило Лопиталя, снова получили неопределенность  или
или 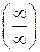 , то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.
, то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.
Задание 8. Построить график функции  используя общую схему исследования функции. Определить абсолютный максимум
используя общую схему исследования функции. Определить абсолютный максимум
и абсолютный минимум функции на отрезке [–1, 2].
Краткие теоретические сведения и образец решения примера сведены в таблицу 1.
Общая схема исследования и построения графика функции 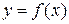
| п/п | Краткие теоретические сведения | Пример |
Область определения функции (о.о.ф.). Областью определенияD(f) функции 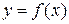 называется множество всех называется множество всех  таких, что выражение f (x) имеет смысл, т. е. взяв любое таких, что выражение f (x) имеет смысл, т. е. взяв любое  и подставив в f (x) можно найти соответствующее значение функции f (x) и подставив в f (x) можно найти соответствующее значение функции f (x)
| 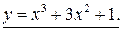
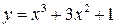 определена для любого х, т. е. о.о.ф. определена для любого х, т. е. о.о.ф.   или или 
| |
 2 2
| Область непрерывности функции. Функция 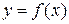 называется непрерывной в точке х 0, если она: 1) определена в точке х 0; 2) имеет конечный предел при называется непрерывной в точке х 0, если она: 1) определена в точке х 0; 2) имеет конечный предел при 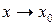 ; 3) этот предел равен значению функции в этой точке ; 3) этот предел равен значению функции в этой точке 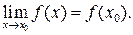 Функция называется непрерывной на некотором промежутке Х, если она непрерывна в каждой точке этого промежутка.
Точка х 0 называется точкой разрыва функции, если в этой точке не выполнено хотя бы одно из условий 1—3 непрерывности функции. Все элементарные функции непрерывны во всех точках, где они определены.
Функция называется непрерывной на некотором промежутке Х, если она непрерывна в каждой точке этого промежутка.
Точка х 0 называется точкой разрыва функции, если в этой точке не выполнено хотя бы одно из условий 1—3 непрерывности функции. Все элементарные функции непрерывны во всех точках, где они определены.
| Так как функция 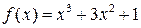 определена на всей числовой оси, то она и непрерывна для любого определена на всей числовой оси, то она и непрерывна для любого  Точек разрыва нет.
Точек разрыва нет.
|
Исследовать функцию на чётность, нечётность.
Функция 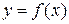 называется чётной, если называется чётной, если  , её график симметричен относительно оси ОY.
Функция , её график симметричен относительно оси ОY.
Функция 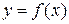 называется нечётной, если называется нечётной, если  , её график симметричен относительно начала координат. Остальные функции называются функциями общего вида. , её график симметричен относительно начала координат. Остальные функции называются функциями общего вида.
| 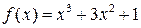


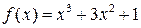 — общего вида — общего вида
|
Определить (если возможно) точки пересечения графика функции с осями координат. Для этого решить системы:
Пересечение с осью OY 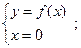 пересечение с осью ОХ пересечение с осью ОХ 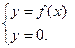
| 
 решение затруднено.
решение затруднено.
| |||||||||||||||||||||
 5 5
| Определить асимптоты графика функции. Асимптотой кривой 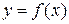 называется прямая l, такое, что расстояние точки называется прямая l, такое, что расстояние точки  от этой прямой стремится к нулю при неограниченном удалении точки по кривой от начала координат. Различают вертикальные и наклонные асимптоты.
Прямая от этой прямой стремится к нулю при неограниченном удалении точки по кривой от начала координат. Различают вертикальные и наклонные асимптоты.
Прямая  является вертикальной асимптотой графика функции является вертикальной асимптотой графика функции 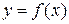 , если х 0 есть точка бесконечного разрыва функции, т. е. если хотя бы один из односторонних пределов функции , если х 0 есть точка бесконечного разрыва функции, т. е. если хотя бы один из односторонних пределов функции  Прямая
Прямая  есть наклонная асимптота графика функции есть наклонная асимптота графика функции 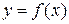 , если , если  причем оба предела существуют и конечны. причем оба предела существуют и конечны.
| Т. к. функция 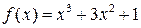 не имеет точек разрыва, то вертикальных асимптот у графика функции нет. не имеет точек разрыва, то вертикальных асимптот у графика функции нет.
 Наклонных асиптот нет.
Наклонных асиптот нет.
| ||||||||||||||||||||
Определить интервалы монотонности и точки локального экстремума функции. Функция 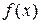 называется возрастающей на (а, b) называется возрастающей на (а, b)  если для если для  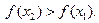 Функция Функция 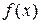 называется убывающей на (а, b) называется убывающей на (а, b)  если для если для 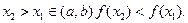 Функция называется монотонной на (а, b), если Функция называется монотонной на (а, b), если 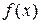 только только 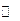 или только или только 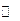 на (а, b).
Если для всех на (а, b).
Если для всех  то то 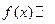 на (а, b). на (а, b).
 то то 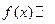 на (а, b). на (а, b). | а) Определим критические точки:
 б) о.о.ф. найденными критическими точками разбиваем на интервалы и определяем знак
б) о.о.ф. найденными критическими точками разбиваем на интервалы и определяем знак 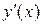 внутри каждого внутри каждого
| |||||||||||||||||||||

| Точка  называется точкой локального максимума (max), [минимума (min)] функции называется точкой локального максимума (max), [минимума (min)] функции 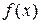 , если существует некоторый интервал , если существует некоторый интервал  содержащий точку х 0 такой, что для всех содержащий точку х 0 такой, что для всех   Точки локального максимума и локального минимума называются точками локального экстремума функции.
Необходимое условие экстремума. Если х 0 точка локального экстремума непрерывной функции
Точки локального максимума и локального минимума называются точками локального экстремума функции.
Необходимое условие экстремума. Если х 0 точка локального экстремума непрерывной функции 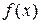 , то её первая производная , то её первая производная  в точке х 0 или равна нулю, или не существует.
Точки, в которых в точке х 0 или равна нулю, или не существует.
Точки, в которых 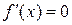 или или  не существует, называются критическими точками. Первое достаточное условие экстремума: если при переходе через критическую точку х 0 знак не существует, называются критическими точками. Первое достаточное условие экстремума: если при переходе через критическую точку х 0 знак  изменился
с «+» на «–», то в точке х 0 локальный максимум;
с «–» на «+», то в точке х 0 локальный минимум;
если знак изменился
с «+» на «–», то в точке х 0 локальный максимум;
с «–» на «+», то в точке х 0 локальный минимум;
если знак  не изменился, то в точке х 0 экстремума нет. не изменился, то в точке х 0 экстремума нет.
|
| ||||||||||||||||||||
Определить интервалы выпуклости функции, точки перегиба
Функция 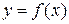 называется выпуклой вверх называется выпуклой вверх  [ вниз [ вниз  ] на интервале (а, b), если для любых ] на интервале (а, b), если для любых 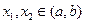 выполняется неравенство: выполняется неравенство:
 Точки, разделяющие интервалы выпуклости, называются точками перегиба.
Если
Точки, разделяющие интервалы выпуклости, называются точками перегиба.
Если  всюду на (а, b), то функция всюду на (а, b), то функция 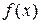 выпукла вниз ( выпукла вниз ( ) на (а, b).
Если ) на (а, b).
Если  всюду на (а, b), то функция всюду на (а, b), то функция 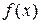 выпукла вверх выпукла вверх  на (а, b). на (а, b).
| а) Определим точки, подозрительные на перегиб:
 б) О.о.ф. найденными точками разбиваем на интервалы, определяем знак
б) О.о.ф. найденными точками разбиваем на интервалы, определяем знак 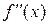 внутри каждого интервала. внутри каждого интервала.

| |||||||||||||||||||||
Необходимое условие перегиба: если х 0 — абсцисса точки перегиба непрерывной функции 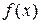 , то , то  или или  не существует.
Достаточное условие точки перегиба: пусть не существует.
Достаточное условие точки перегиба: пусть  или или  не существует. Тогда если при переходе через х 0 знак второй производной не существует. Тогда если при переходе через х 0 знак второй производной 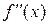 изменился, то изменился, то 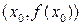 точка перегиба графика функции (при этом точка перегиба графика функции (при этом  существует). существует).
|
| |||||||||||||||||||||
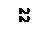 8 8
| Построить график. Для построения графика можно взять несколько дополнительных точек (–3, 1), (1, 5). |

| ||||||||||||||||||||
Абсолютным (или глобальным) экстремумом функции называется наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значения функции в области.
Если функция непрерывна на отрезке [ a, b ], то она всегда имеет на этом отрезке абсолютный максимум и абсолютный минимум.
Абсолютный экстремум может быть или в точках локального экстремума Î [ a, b ] или в концевых точках отрезка.
Если дифференцируемая функция на интервале (а, b) имеет единственную точку локального экстремума, то эта точка будет и точкой абсолютного экстремума функции на (а, b).
 Пример. Пример. 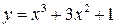 на [–1; 2] на [–1; 2]
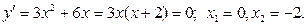
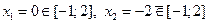
 Следовательно: Следовательно:  — абсолютный минимум; — абсолютный минимум;
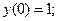  — абсолютный максимум — абсолютный максимум
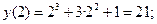 функции на [–1; 2]. функции на [–1; 2].
|