Квантталған сигналдарды кодалау

Кода негізі рұ қ сат етілген дең гей санына (кванттау дең гейлері) тең жә не кодалық топтағ ы символдар саны бірге тең квантталғ ан АИМ-2 сигналын кодалық деп санауғ а болады. Осылайша, квантталғ ан сигнал кө п дең гейлі болып табылады.

Кө п дең гейлі сигналдарды беру ө те ың ғ айсыз, ө йткені қ абылдағ ыш барлық рұ қ сат етілген дең гейлерді ажыратуы тиіс. Оғ ан қ оса бұ ндай сигналдарды, егер оларғ а бө геуілдер ә сер етсе, қ алпына келтіру (регенерациялау) ө те қ иын. Басқ а сө збен айтқ анда, кө п дең гейлі сигналдарғ а аналогты сигналдардың кемшіліктері сә йкес келеді. Сондық тан ЦБЖ кө бінесе негіздері салыстырмалы тү рде кіші кодалар қ олданылады, кө бінесе екілік кодалар қ олданылады. кө п дең гейлі сигналды негізі кіші кодағ а тү рлендң ру процессін кодалау деп атайды. Символдар (жіберулер, цифрлар) комбинациясы кодалау нә тижесі болып табылады. Олар сә йкес есептеу жү йесінде квантталғ ан сигнал дең гейінің рұ қ сат етілген номерін кө рсетеді. ИКМ-АУБ ЦБЖда екілік есептеу жү йесі кең қ олданыс тапты. Кез келген рұ қ сат етілген дең гейі бар квантталғ ан дең гейлерді екілік есептеу жү йесінде жазуды келесі тү рде кө рсетуге болады:

(2.2)

мұ ндағ ы - кода разрядының саны; 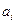- разрядты цифра, ол 0 немесе 1 мағ ынасын қ абылдайды. m-разрядты екілік кода кө мегімен, тең кванттау дең гейлерінің санын кодалауғ а болады.

Кванттау дең гейінің санының таң далуы кванттау қ адамының мү мкін шамасыен анық талатындық тан, кө бінесе кері есепті шешуге тура келеді: кода разрядының минималды қ ажетті санын анық тау, ол белгілі болғ ан жағ дайда кодалау ү шін қ олданылуы мү мкін. Сондық тан екілік кода ү шін мына ө рнек қ олданылады:

(2.3)

мұ ндағ ы 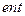дө ң гелек жақ шадағ ы ө рнектен ү лкен бү тін.

Кодалық топтардың немесе кодалық комбинациялардың жалпы саны .

Бірегей қ ұ рылу заң ымен байланысқ ан, қ олданылатын кодалық комбинациялардың кө птігі кода деп аталады. Қ ұ рылу негізінде (2.2) қ атынасы жатқ ан кода, қ арапайым кода болып табылады жә не натуралды екілік кода деп аталады.

Графикалық тү рде кодаларды кодалық кестелермен немесе кодалық растрлармен бейнелеу ың ғ айлы, олар кванттау дең гейлерін жә не оларғ а сә йкес кодалық комбинациялардың байланысын сипаттайды. Осылайша, оларды дең гейлері бойынша сипаттауғ а мү мкіндік туады. ЦБЖ - да кең інен қ олданылатын кодалардың кодалық кестелері 2.3 суретте кө рсетілген.

2.3, а суретінде 4-разрядты натуралды екілік коданың кодалық кестесі кө рсетілген, оның кө мегімен 16 дең гейдің берілуін іске асыруғ а болады. Бұ л жердегі кодалық кестенің қ араң ғ ы телімдер 1 (бірлер немесе импульстар), ал ашық телімдер - 0 (нольдер немесе пробелдер) білдіреді. Дең гей номреленуі жоғ арыдан тө мен қ арай берілген, жоғ арыда кода разрядының салмағ ы кө рсетілген.

Сурет 2.3 – Екілік кодалардың кестелері: а — натуралды; б - Грея кодасы; в – симметриялық кода

Кодалық комбинацияның жү ру ретін керіге алмастыру қ арапайым кері коданы береді, оның разрядының салмағ ы тө менде кө рсетілген. Мысалы, дең гей натуралды кодада 1011 кодалық комбинация тү рінде ұ сынылады (сурет 2.3, а), оның кері кодасы 1101 тү рде болады.

Кодалық комбинацияда барлық импульстарды пробелге ауыстыру (немесе бірлерді нольге, ал нольді бірлерге) инверсты кодағ а ә келеді. Мысалы, кодалық комбинациясы инверсты кодада 0100 тү рге ие болады. ЦБЖ –да қ олданылатын коданың тағ ы бір тү рі Грей кодасы (рефлексты немесе айналық кода деп те атайды). Оның айрық ша ерекшелігі: кез келген екі кө рші кодалық комбинация бір бірінен тек қ ана бір разрядқ а айрық шаланады (сурет 2.3, б). Грей кодасы негізінен топтық телефондық жә не кең жолақ ты теледидар сигналдарын кодалау ү шін қ олданылады, бұ л сигналдар ү шін кванттау дең гейідегі кө ршілес кодалық топтардың кө п разряд сандарының символдарындағ ы айырмашылық болмауы қ ажет, ө йткені бұ л жағ дайда кодалау жә не декодалау кезіндегі қ ателіктер ө те қ ауіпті. Бірақ Грей кодасын декодалау ө те қ иын. Сондық тан оны кө бінесе натуралды екілік кодағ а тү рлендіреді, содан кейін ғ ана декодалайды, ө йткені натуралды кілік коданы декодалау қ иын емес. Грей кодасының қ ұ рылу тә ртібі келесідей жү реді: бірінші разрядтар кө рші дең гейлердің 2ⁱ блоктарды нақ ты анық тайды, ол блоктар табалдырық арқ ылы бө лінген, ал i-шы разряд барлық табалдырық тарда бірден нольге немесе нольден бірге ө туді кө рсетеді, олар алдың ғ ы разрядтардың ө туімен ә лі анық талмағ ан болады.

Грей кодасының натуралды екілік кодағ а тү рленуі келесі тү рде жү реді.

Егер екілік натуралды коданың разрядын арқ ылы, ал Грей кодасының разрядын арқ ылы белгілесе, онда:

Соң ғ ы ө рнектің оң жаң ындағ ы символы 2 модулі бойынша қ осуды білдіреді, ал бұ л операция ерекше НЕМЕСЕ логикалық функциясымен бірдей, ол соң ғ ы ө рнектің орта жағ ында кө рсетілген, бұ л ереже барлық келесі разрядтар ү шін де жү реді, мысалы:

Натуралды екілік коданың жә не Грей коданың кестелерін салыстыру Грей кодасын натуралды кодағ а тү рлендірудің оң ай ережесін кө рсетеді: натуралды коданың i-шы разрядында импульс немесе пробел қ ұ рылады, импульстың немесе пробелдың қ ұ рылуы алдың ғ ы Грей кодасының (i-шы позицияны қ осқ анда) комбинациясындағ ы импульсты позициясында импульстардың саны жұ п немесе тақ болуына байланысты болады. Мысалы, Грей кодасының 1011001 комбинациясы осы ережеге сә йкес натуралды коданың 1101110 комбинациясына сә йкес келеді. Импульс сандарының жұ п немесе тақ тығ ын анық тау операциясы триггер кө мегімен жасауғ а болады.

Санауларды кодалауда симметриялы кодалар кең қ олданысқ а ие (сурет 2.3, в). екі полярлы кванттталғ ан санауларды кодалау барысында санаудың полярлығ ын белгілеу ү шін натуралды екілік коданың жоғ арғ ы разрядын қ олдану ың ғ айлы, мысалы 1 оң санауды кодалау ү шін жә не 0 – теріс санауды кодалау ү шін, ал қ алғ ан разрядтар абсолютты шамаларды кодалау ү шін. Симметриялы коданың кестесі ө зінің ортасына қ атысты симметриялы болады. 2.3, б суреттен Грей кодасы симметриялық қ асиетке ие екені анық.

2.4 суретте тө рт разрядты натуралды екілік кода қ олданғ андағ ы квантталғ ан топтық АИМ сигналдың кодалану процессін кө рсететін, уақ ыттық диаграммасы келтірілген.

Кодалайтын қ ұ рылғ ының (кодер) кірісіне тү сетін, санау амплитудалары 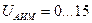диапазонында шартты кванттау қ адамының мағ ынасын қ абылдайды, ал кодердің шығ ысында цифрлық сигналы қ ұ рылады, ол сигнал тө рт разрядты кодалық комбинацияның кезектілігін ұ сынады. Кодер шығ ысындағ ы m-разрядты кодалық комбинацияның кезектілігі импульсты – кодалы модуляцияланғ ан топтық сигнал болады, оны цифрлық деп атайды.

Сурет 2.4 - U_АИМ санауларының U_ИКМ кодалық комбинацияғ а кодалану процессі

Кодалардың негізгі сипаттамалары келесілер:

- кодалық қ ашық тық, бұ л разрядтар саны, бұ ларда кодалық комбинация ө зара айрық шаланады; мысалы, бірінің соң ынан бірі жү ретін, натуралды екілік кода (сурет 2.1, а) дең гейлерінің арасындағ ы қ ашық тық 1, 2, 1, 3, 1, 2, 1, 4 жә не т.б. тең болады. m-разрядты натуралды коданың кө ршілес дең гейлерінің арасындағ ы ең ү лкен қ ашық тық тең жә не кодалық кестенің ортасынан орын алады. Бірлі қ ашық тық ты кодада кө ршілес кодалық комбинациялар арасындағ ы айырмашық ыл бірге тең жә не тек қ ана бір разрядтан орын алады. грей кодасы осындай кода болып табылады;

- кода артық тығ ы, берілген кода разрядтылығ ында максималды мү мкін кодалық комбинациялардың іс жү зінде қ олданылатын комбинацияларғ а қ атынасы. комбинациялардың барлық ансамблін колданатын кода (сурет 2.1), артық тық сыз болады;

- кодалық комбинацияның диспаритеттігі, яғ ни бірлердің нольдерден кө п болуы, мысалы 000110 жә не 100111 комбинациялары сә йкесінше - 2 жә не + 2 диспаритерліктерге. Диспаритерлік неғ ұ рлым тө мен болса, соғ ұ рлым ақ параттық сигналдарды синхрондау проблемасын шешу оң ай болады;

- қ ателіктерді анық тау мү мкіндігі, яғ ни кодалық комбинацияның қ ұ рылымының ө згеруі бойынша қ ателіктердің барлығ ы жө нінде шешім қ абылдауғ а болады. Тұ рақ ты дипаритерлігі бар қ ода ү шін кодалық комбинацияның разрядтарының біреуінің бұ рмалануы кезінде диспаритерліктің ө згеруі болады, бұ л қ абылдауда қ олданылатын кодалық комбинациялардың ансамбліне кірмейтін кодалық комбинацияның пайда болуына ә келеді, бұ л яғ ни қ ате бар екенін айтады. Егер 7-разрядты кодалық комбинацияда 4 бірлік жә не 3 ноль болса, кез келген бірлі қ ате бірліктердің тақ санын кө рсетеді. Сондық тан, осындай қ атенің бар екенін немесе жоқ екенін анық тау ү шін, қ абылданатын бірліктердің жұ п сан немесе тақ сан екенін анық тау қ ажет. Бұ л ә діс жұ птық қ а тексеру деп аталады;

-қ ателерді тү зету мү мкіндігі, яғ ни кодалық комбинацияның қ ұ рылымының ө згеруі бойынша жә не сә йкес кодалық комбинациялар арасындағ ы кодалық қ ашық тық бойынша қ ателер анық талады жә не жойылады.

Кодалау желілі жә не желісіз болуы мү мкін. Желілі кодалау деп бір қ алыпты квантталғ ан сигналды кодалауды айтады, ал желісіз – бір қ алыпсыз квантталғ ан сигналды кодалау. Кодалау жеке квантталғ ан АИМ сигнал дең гейінде жә не топтық квантталғ ан АИМ сигнал дең гейінде іске асуы мү мкін. Бірінші жағ дайда кодек жеке болса, екінші жағ дайда топтық болады. Бірақ екі кодалау ә дістерінде де міндетті тү рде топтық ИКМ сигнал қ ұ рылады, ол сигнал цикл деп аталатын, дискретизация периодында анық талады.