
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Список задач контрольной работы № 3
|
|
1. Исследовать сходимость числового ряда.
1.1. 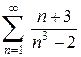 . 1.2.
. 1.2.  .
.
1.3. 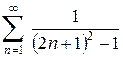 . 1.4.
. 1.4.  .
.
1.5. 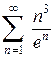 . 1.6.
. 1.6. 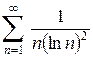 .
.
1.7.  . 1.8.
. 1.8.  .
.
1.9.  . 1.10.
. 1.10.  .
.
2. Найти интервал сходимости степенного ряда.
2.1. 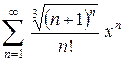 . 2.2.
. 2.2. 
2.3.  . 2.4.
. 2.4.  .
.
2.5.  . 2.6.
. 2.6. 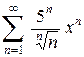 .
.
2.7.  . 2.8.
. 2.8.  .
.
2.9.  . 2.10.
. 2.10.  .
.
3. Вычислить определенный интеграл  с точностью до 0, 001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
с точностью до 0, 001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
3.1.  . 3.2.
. 3.2.  .
.
3.3.  . 3.4.
. 3.4.  .
.
3.5.  . 3.6.
. 3.6.  .
.
3.7.  . 3.8.
. 3.8.  .
.
3.9.  . 3.10.
. 3.10.  .
.
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения у = у (х) дифференциального уравнения у' = f (х, y), удовлетворяющего начальному условию у (0) = у 0.
4.1. у' = cos x + y 2; у (0) = 1.
4.2. у' = ex + y 2; у (0) = 0.
4.3. у' = y + y 2; у (0) = 3.
4.4. у' = 2 ey - xy; у (0) = 0.
4.5. у' = sin x + y 2; у (0) = 1.
4.6. у' = ex + y; у (0) = 4.
4.7. у' = x 2 + y 2; у (0) = 2.
4.8. у' = sin x + 0, 5 y 2; у (0) = 1.
4.9. у' = 2 ey + xy; у (0) = 0.
4.10. у' = x + x 2 + y 2; у (0) = 5.
5. Разложить данную функцию f (х) в ряд Фурье в интервале (a; b).
5.1. f (х) = x + 1 в интервале (-p, p).
5.2. f (х) = x 2 + 1 в интервале (-2, 2).
5.3. f (х) =  в интервале (-p, p).
в интервале (-p, p).
5.4. f (х) = 1 + | x | в интервале (-1, 1).
5.5. f (х) =  в интервале (-p, p).
в интервале (-p, p).
5.6. f (х) = |1 - x | в интервале (-2, 2).
5.7. f (х) = | x | в интервале (-p, p).
5.8. f (х) = x - 1 в интервале (-1, 1).
5.9. f (х) = x 2 в интервале (0, 2p).
5.10. f (х) =  в интервале (-p, p).
в интервале (-p, p).
6. Найти общее решение дифференциального уравнения.
6.1. (х 2 - у 2) у ' = 2 ху. 6.2. (1 + х 2) у ' - 2 ху = (1 + х 2)2.
6.2. ху ' =  . 6.4. ху ' + у - 3 = 0.
. 6.4. ху ' + у - 3 = 0.
6.5. ху ' +  - у = 0. 6.6. у ' cos x = (у + 1) sin x.
- у = 0. 6.6. у ' cos x = (у + 1) sin x.
6.7. ху ' - у =  . 6.8. х 2 у ' = 2 ху + 3.
. 6.8. х 2 у ' = 2 ху + 3.
6.9. х 2 у ' + у 2 - 2 ху = 0. 6.10. ху ' + у - х - 1 = 0.
7. Найти частное решение дифференциального уравнения
y " + py ' + qy = f (x), удовлетворяющее начальным условиям: у (0) = у 0,
у' (0) =  .
.
7.1. y " + 4 y ' - 12 y = 8 sin 2 x; у (0) = 0, у' (0) = 0.
7.2. y " - 6 y ' + 9 y = x 2 - x + 3; у (0) = 4/3, у' (0) = 1/27.
7.3. y " + 4 y = е- 2 х ; у (0) = 0, у' (0) = 0.
7.4. y " - 2 y ' + 5 y = xе 2 х ; у (0) = 1, у' (0) = 0.
7.5. y " + 5 y ' + 6 y = 12 cos 2 x; у (0) = 1, у' (0) = 3.
7.6. y " - 5 y ' + 6 y = (12 х - 7) е - х; у (0) = 0, у' (0) = 0.
7.7. y " - 4 y ' + 13 y = 26 x + 5; у (0) = 1, у' (0) = 0.
7.8. y " - 4 y ' = 6 x 2 + 1; у (0) = 2, у' (0) = 3.
7.9. y " - 2 y ' + y = 16 ех; у (0) = 1, у' (0) = 2.
7.10. y " + 6 y ' + 9 y = 10 е -3 х ; у (0) = 3, у' (0) = 2.
8. Элементы теории вероятностей и математической статистики.
8.1. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
8.2. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
8.3. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0, 9, вторым – 0, 8, третьим – 0, 7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
8.4. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
8.5. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равно 0, 9, второе – 0, 95, третье – 0, 85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.
8.6. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
8.7. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наугад взятых из этой партии, ровно 3 окажутся дефектными.
8.8. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
8.9. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной рана 0, 7, если она изготовлена на первом станке, 0, 8 – если на втором, 0, 9 – если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
8.10. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наугад по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
9. Дискретная случайная величина Х может принимать только два значения: х 1 и х 2, причем х 1 < х 2. Известны вероятность р 1 возможного значения х 1, математическое ожидание М (Х) и дисперсия D (Х). Найти закон распределения этой случайной величины.
9.1. р 1 = 0, 1; М (Х) = 3, 9; D (Х) = 0, 09.
9.2. р 1 = 0, 3; М (Х) = 3, 7; D (Х) = 0, 21.
9.3. р 1 = 0, 5; М (Х) = 3, 5; D (Х) = 0, 25.
9.4. р 1 = 0, 7; М (Х) = 3, 3; D (Х) = 0, 21.
9.5. р 1 = 0, 9; М (Х) = 3, 1; D (Х) = 0, 09.
9.6. р 1 = 0, 9; М (Х) = 2, 2; D (Х) = 0, 36.
9.7. р 1 = 0, 8; М (Х) = 3, 2; D (Х) = 0, 16.
9.8. р 1 = 0, 6; М (Х) = 3, 4; D (Х) = 0, 24.
9.9. р 1 = 0, 4; М (Х) = 3, 6; D (Х) = 0, 24.
9.10. р 1 = 0, 2; М (Х) = 3, 8; D (Х) = 0, 16.
10. Случайная величина Х задана функцией распределения F (x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
10.1. F (x) = 
10.2. F (x) = 
10.3. F (x) = 
10.4. F (x) = 
10.5. F (x) = 
10.6. F (x) = 
10.7. F (x) = 
10.8. F (x) = 
10.9. F (x) = 
10.10. F (x) = 
Приложение
МИНОБРНАУКИ РОССИИ
Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Самарский государственный технический университет» в г. Сызрани
Кафедра ОТД
КОНТРОЛЬНАЯ РАБОТА № 3
по дисциплине " Математика"
на тему " Ряды. Дифференциальные уравнения.
Элементы теории вероятностей"
Выполнил
студент группы _______
_____________________
(Ф.И.О.)
Проверил
к.п.н., доцент
Егорова И.П.
Сызрань, 2012