Происхождение энергии деления тяжёлых ядер.

Хорошо известно, что энергия деления тяжёлых ядер, которая используется в практических целях – это кинетическая энергия осколков исходных ядер (см., например, [М3]). Но каково происхождение этой энергии, т.е. какая энергия превращается в кинетическую энергию осколков?

Официальные воззрения на этот вопрос отличаются крайней непоследовательностью. Так, Мухин [М3] пишет, что большая энергия, освобождаемая при делении тяжёлого ядра, обусловлена разностью дефектов масс у исходного ядра и осколков – и получает, на основе этой логики, оценку выхода энергии при делении ядра урана:»200 МэВ. Но далее он пишет, что в кинетическую энергию осколков превращается энергия их кулоновского отталкивания – которая, когда осколки находятся впритык друг к другу, составляет те же»200 МэВ [М3]. Близость обеих этих оценок к экспериментальному значению, конечно, впечатляет, но уместен вопрос: в кинетическую энергию осколков превращается всё-таки разность дефектов масс или энергия кулоновского отталкивания? Вы уж определитесь, про что нам рассказываете – про бузин у или про дядьку в Киеве!

Эту тупиковую дилемму теоретики создали сами: по их логике, им непременно требуется и разность дефектов масс, и кулоновское отталкивание. Откажись либо от того, либо от другого – и станет совсем очевидна никчёмность традиционных исходных предпосылок в физике ядра. Вот, например, зачем говорят о разности дефектов масс? Затем, чтобы хоть как-то объяснить саму возможность феномена деления тяжёлых ядер. Нас пытаются убедить в том, что деление тяжёлых ядер происходит потому, что оно энергетически выгодно. Что за чудеса? При делении тяжёлого ядра, часть ядерных связей разрушается – а энергии ядерных связей исчисляются МэВами! Нуклоны в ядре связаны на порядки сильнее, чем атомарные электроны. И опыт учит нас, что система устойчива как раз в области энергетической выгодности – а если бы ей было энергетически выгодно распасться, она распалась бы немедленно. Но залежи урановых руд в природе существуют! О какой же «энергетической выгодности» деления ядер урана может идти речь?

Чтобы абсурдность допущения о выгодности деления тяжёлого ядра не слишком бросалась в глаза, теоретики пустились на отвлекающий манёвр: они рассуждают об этой «выгодности» в терминах средней энергии связи, приходящейся на один нуклон. Действительно, с увеличением атомного номера, увеличивается и величина дефекта масс у ядра, но число нуклонов в ядре увеличивается быстрее – за счёт избыточных нейтронов. Поэтому у тяжёлых ядер полная энергия связи, пересчитанная на один нуклон, уменьшается с увеличением атомного номера. Казалось бы, тяжёлым ядрам делиться, в самом деле, выгодно? Увы, эта логика основана на традиционных представлениях о том, что ядерными связями охвачены все нуклоны в ядре. При таком допущении, средняя энергия связи на нуклон E ₁ есть частное от деления энергии связи ядра D E на число нуклонов [М3]:

E ₁=D E / A, D E =(Zm _p+(A-Z) m_n) c ²-(M _ат- Zm_e) c ², (4.13.1)

где Z - атомный номер, т.е. число протонов, A - число нуклонов, m _p, m_n и m_e – массы, соответственно, протона, нейтрона и электрона, M _ат - масса атома. Однако, неадекватность традиционных представлений о ядре мы уже проиллюстрировали выше (4.11). И если, по логике предложенной модели (4.12), при расчёте энергии связи на нуклон не учитывать те нуклоны в ядре, которые временно не охвачены ядерными связями, то мы получим формулу, отличную от (4.13.1). Если считать, что текущее число связанных нуклонов составляет 2 Z (4.12), и что каждый из них связан лишь половину времени действия связи (4.12), то для средней энергии связи на нуклон мы получим формулу

E ₁^*=D E / Z, (4.13.2)

которая отличается от (4.13.1) лишь знаменателем. Сглаженные функции E ₁(Z) и E ₁^*(Z) приведены на Рис.4.13. В отличие от привычного графика E ₁(Z), помещённого во многие учебники, график E ₁^*(Z) имеет поразительную особенность: он демонстрирует, для тяжёлых ядер, независимость энергии связи на нуклон от числа нуклонов. Значит, из нашей модели (4.12) следует, что ни о какой «энергетической выгодности» деления тяжёлых ядер не может быть и речи – в согласии со здравым смыслом. Т.е., кинетическая энергия осколков не может быть обусловлена разностью дефектов масс исходного ядра и осколков.

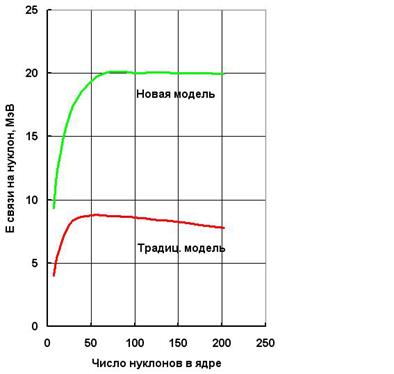
Рис.4.13

В согласии с тем же здравым смыслом, в кинетическую энергию осколков не может превращаться энергия их кулоновского отталкивания: мы привели как теоретические аргументы (4.7, 4.12), так и экспериментальные свидетельства (4.12) о том, что никакого кулоновского отталкивания у частиц, входящих в состав ядра, не существует.

Тогда каково же происхождение кинетической энергии осколков тяжёлого ядра? Прежде постараемся ответить на вопрос: почему, при цепной ядерной реакции, деления ядер эффективно вызываются нейтронами, вылетевшими при предыдущих делениях – причём, нейтронами тепловыми, т.е. имеющими энергии, ничтожные по ядерным масштабам. С тем, что тепловые нейтроны обладают способностью разваливать тяжёлые ядра, казалось бы, трудно согласовать наш вывод о том, что «избыточные» - на текущий момент – нейтроны в тяжёлых ядрах являются свободными (4.12). Тяжёлое ядро буквально нашпиговано тепловыми нейтронами, но при этом оно отнюдь не распадается – хотя его немедленное деление вызывает попадание в него единственного теплового нейтрона, испущенного при предыдущем делении.

Логично допустить, что временно свободные тепловые нейтроны в тяжёлых ядрах и тепловые нейтроны, испускаемые при делении тяжёлых ядер, всё-таки отличаются друг от друга. Поскольку у тех и у других отсутствуют ядерные прерывания, то степенью свободы, по которой они могут различаться, должен обладать процесс, обеспечивающий внутреннюю связь в нейтроне – через циклические превращения входящих в его состав пар (4.10). И единственная степень свободы, которую мы здесь усматриваем – это возможность ослабления этой внутренней связи «на приросте масс» (4.10), из-за уменьшения частоты циклических превращений в нейтроне – с излучением соответствующих g-квантов. Приведение нейтронов в подобное ослабленное состояние – например, при распадах тяжёлых ядер, когда происходят экстремальные превращения энергии из одних форм в другие – не представляется нам чем-то необычным. Ослабленное состояние нейтрона обусловлено, по-видимому, нештатным режимом работы программы, которая формирует нейтрон в физическом мире – и при этом нейтрону легче распасться на протон и электрон. Похоже, что среднее время жизни в 17 мин, измеренное для нейтронов, вылетающих из ядерных реакторов [М3, К7], характерно как раз для ослабленных нейтронов. Неослабленный же нейтрон способен жить, на наш взгляд, пока работает связующий его алгоритм (4.10), т.е., неопределённо долго.

Каким же образом ослабленный нейтрон разваливает тяжёлое ядро? По сравнению с неослабленными нейтронами, у ослабленных нейтронов период прерываний нуклонных пульсаций увеличен. Если у такого нейтрона, попавшего в ядро, будут «включены» ядерные прерывания, так что он окажется связан с каким-либо протоном, то вышеописанный синхронизм переключения связей в тройке n ⁰- p ⁺- n ⁰ (4.12) окажется невозможен. В результате нарушится синхронизм связей в соответствующем a-комплексе, что вызовет последовательность сбоев переключений связей, оптимально переформировывающих a-комплексы и обеспечивающих динамическую структуру ядра (4.12). Образно говоря, через ядро пройдёт трещина, порождаемая не силовым разрывом ядерных связей, а нарушениями синхронизма их переключений. Заметим, что ключевым моментом для описанного сценария является «включение» у ослабленного нейтрона ядерной связи – а для того, чтобы это «включение» произошло, нейтрон должен иметь достаточно малую кинетическую энергию. Так мы объясняем, почему нейтроны с кинетической энергией в несколько сотен кэВ только возбуждают тяжёлое ядро, а тепловые нейтроны с энергиями всего в несколько сотых эВ способны эффективно его развалить.

Что же мы видим? При делении ядра на два осколка, «аварийно» рассыпаются те ядерные связи, которые, в штатном режиме своих переключений (4.12), сцепляли эти два осколка в исходном ядре. Возникает нештатная ситуация, при которой собственные энергии некоторых нуклонов уменьшены на величину энергии ядерных связей, но самих этих связей уже нет. Эта нештатная, по логике принципа автономных превращений энергии (4.4), ситуация немедленно исправляется следующим образом: собственные энергии нуклонов остаются как есть, а бывшие энергии распавшихся связей превращаются в кинетическую энергию нуклонов – и, в конечном счёте, в кинетическую энергию осколков. Таким образом, энергия деления тяжёлого ядра обусловлена не разностью дефектов масс у исходного ядра и осколков, и не энергией кулоновского отталкивания осколков. Кинетическая энергия осколков – это бывшая энергия ядерных связей, удерживавших эти осколки в исходном ядре. В пользу этого вывода свидетельствует поразительный и малоизвестный факт постоянства кинетической энергии осколков – в независимости от силы воздействия, инициирующего деление ядра. Так, при инициировании деления ядер урана протонами с энергией 450 МэВ, кинетическая энергия осколков составляла 163±8 МэВ [Б2], т.е. столько же, сколько и при инициировании деления тепловыми нейтронами, с энергиями в сотые доли эВ!

Сделаем, на основе предложенной модели, ориентировочную оценку энергии деления ядра урана по наиболее вероятному варианту, ₉₂U²³⁵®₃₆Kr⁹⁴+₅₆Ba¹³⁹, при котором осколки включают в себя 18 и 28 a-комплексов. Если считать, что эти 18 и 28 a-комплексов были сцеплены в исходном ядре с помощью 8-10 переключаемых связей, со средней энергией 20 МэВ каждая (см. Рис.4.13), то энергия осколков должна составить 160-200 МэВ, т.е. величину, близкую к фактической [М3].