
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 2.2
|
|
Табличная функция Лапласа (см приложение А).
Проверим гипотезу с помощью критерия согласия Хи-квадрат Пирсона.
Параметр  = 71, 665,
= 71, 665,  6, 677 (вычислены в лабораторной работе №1).
6, 677 (вычислены в лабораторной работе №1).
Вычислим вероятности по формуле:
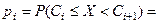


 = =
= =  = -0, 3997+0, 5 = 0, 1003,
= -0, 3997+0, 5 = 0, 1003,

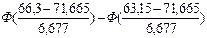 = =
= =  = - 0, 2881 + 0, 3997 = 0, 1116,
= - 0, 2881 + 0, 3997 = 0, 1116,

 = =
= =  = - 0, 1293 + 0, 2881= 0, 1588,
= - 0, 1293 + 0, 2881= 0, 1588,

 = =
= =  = 0, 0557 + 0, 1293 = 0, 1850,
= 0, 0557 + 0, 1293 = 0, 1850,

 = =
= = 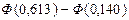 = 0, 2291- 0, 0557 = 0, 1734,
= 0, 2291- 0, 0557 = 0, 1734,

 = =
= =  = 0, 3599- 0, 2291 = 0, 1308,
= 0, 3599- 0, 2291 = 0, 1308,

 = =
= =  = 0, 5 - 0, 3599 = 0, 1401.
= 0, 5 - 0, 3599 = 0, 1401.
Таблица 2.2 – Расчет c2 для случайной величины Х, распределенной по нормальному закону
Границы интервалов

| Частоты эмпири-ческие 
| Вероятности

| Частоты теоретические 
| 
|
( , 63, 15] , 63, 15]
| 0, 1003 | 4, 012 | 0, 985 | |
| (63, 15; 66, 3] | 0, 1116 | 10, 816 | 0, 304 | |
| (66, 3; 69, 45 ] | 0, 1588 | |||
| (69, 45; 72, 6] | 0, 1850 | 19, 568 | 0, 017 | |
| (72, 6; 75, 75] | 0, 1734 | |||
| (75, 75; 78, 9] | 0, 1308 | |||
(78, 9,  ) )
| 0, 1401 | 5, 604 | 0, 028 | |
| итого | 1, 334= 
|

Рисунок 2.2 – Компьютерный расчет
Вывод. По таблицам квантилей распределения c2 определяется критическое значение  =
=  = 3, 841(Приложение Б), соответствующее заданному уровню значимости a=0, 05 и числу степеней свободы
= 3, 841(Приложение Б), соответствующее заданному уровню значимости a=0, 05 и числу степеней свободы  , (4 – число интервалов в последнем столбце таблицы, 2 – число параметров нормального закона распределения). Сравниваем полученное значение с табличным значением. Так как расчетное
, (4 – число интервалов в последнем столбце таблицы, 2 – число параметров нормального закона распределения). Сравниваем полученное значение с табличным значением. Так как расчетное  = 1, 334 меньше, чем табличное
= 1, 334 меньше, чем табличное  = 3, 841, то гипотеза о нормальном законе распределения подтвердилась.
= 3, 841, то гипотеза о нормальном законе распределения подтвердилась.
Пример 2.2
При проведении экспериментов фиксировались значения случайной величины X, характеризующей время простоя оборудования в ожидании ремонта (в часах).
Требуется выдвинуть гипотезу о виде закона распределения данной случайной величины X и проверить ее с помощью критерия согласия  .
.
1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.
Таблица 2.3 – Расчетная таблица
| Номер п/п | Выборка, час. | Вариационный ряд,  , час. , час.
|
| 6, 72 | 0, 21 | |
| 8, 2 | 0, 4 | |
| 0, 4 | 0, 64 | |
| 12, 9 | 0, 69 | |
| 3, 15 | 0, 77 | |
| 34, 5 | 0, 93 | |
| 4, 71 | 1, 14 | |
| 1, 14 | 1, 51 | |
| 2, 87 | 1, 73 | |
| 3, 07 | 1, 86 | |
| 5, 86 | ||
| 11, 4 | 2, 1 | |
| 3, 12 | 2, 32 | |
| 0, 21 | 2, 32 | |
| 1, 51 | 2, 4 | |
| 2, 76 | 2, 76 | |
| 0, 93 | 2, 87 | |
| 2, 4 | 2, 87 | |
| 3, 5 | 2, 99 | |
| 5, 29 | 3, 07 | |
| 1, 86 | 3, 12 | |
| 4, 99 | 3, 15 | |
| 8, 77 | 3, 5 | |
| 1, 73 | 3, 6 | |
| 0, 77 | 4, 59 | |
| 5, 99 | 4, 61 | |
| 7, 95 | 4, 71 | |
| 2, 87 | 4, 99 | |
| 0, 64 | 5, 29 | |
| 5, 74 | 5, 74 | |
| 0, 69 | 5, 86 | |
| 2, 99 | 5, 99 | |
| 4, 59 | 6, 72 | |
| 2, 32 | 7, 95 | |
| 2, 32 | 8, 2 | |
| 8, 77 | ||
| 2, 1 | 11, 4 | |
| 4, 61 | 12, 9 | |
| 30, 1 | 30, 1 | |
| 3, 6 | 34, 5 | |
| Итого |
2) Найдем размах выборки  = 34, 5- 0, 21 = 34, 29.
= 34, 5- 0, 21 = 34, 29.
3) Длина интервала  =
=  =
=  = 5, 424.
= 5, 424.
4) границы интервалов:
 = 0, 21,
= 0, 21,  =0, 21+5, 424 = 5, 634,
=0, 21+5, 424 = 5, 634,  = 5, 634 +5, 424 = 11, 058,
= 5, 634 +5, 424 = 11, 058,  = 11, 058 +5, 424= 16, 482,
= 11, 058 +5, 424= 16, 482,  = 16, 482+ 5, 424= 21, 906,
= 16, 482+ 5, 424= 21, 906, 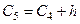 = 21, 906+ 5, 424 = 27, 33,
= 21, 906+ 5, 424 = 27, 33,  = 27, 33+ 5, 424 = 32, 754,
= 27, 33+ 5, 424 = 32, 754,  = 32, 754+ 5, 424 = 38, 178
= 32, 754+ 5, 424 = 38, 178  .
.
5) Построим интервальный статистический ряд:
Таблица 2.4– Интервальный статистический ряд
Границы интервалов  , час. , час.
| Частоты 
|
| [0.21; 5, 634) | |
| [5, 634; 11, 058) | |
| [11, 058; 16, 482) | |
| [16, 482; 21, 906) | |
| [21, 906; 27, 33) | |
| [27, 33; 32, 754) | |
| [32, 754; 38, 178) | |
| Итого |
6) Вычислим необходимые числовые характеристики.
а) математическое ожидание  .
.
7) Построим гистограмму частот.

Рисунок 2.3 – Гистограмма частот
8) По виду гистограммы частот выдвигаем нулевую гипотезу о виде закона распределения случайной величины  (времени простоя оборудования в ожидании ремонта):
(времени простоя оборудования в ожидании ремонта):
 Случайная величина
Случайная величина  (время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.
(время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.
9) Выбираем уровень значимости  .
.
10) Вычислим вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения по формуле: 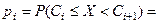

 =
=  .
.
 .
.
Проверим гипотезу с помощью критерия согласия Хи-квадрат Пирсона.
11) Вычислим параметр  =
=  =
=  = 0, 189358 = 0, 189.
= 0, 189358 = 0, 189.
12) Так как изучается непрерывная случайная величина, то при вычислении значений  необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о показательном законе распределения.
необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о показательном законе распределения.
| Вид закона распределения | Первый интервал разбиения | Последний интервал разбиения |
| Экспоненциальный | 
| 
|
13) Вычислим вероятности по формуле  .
.
Пример расчета:
 1- 0, 344788 = 0, 655212 =0, 655.
1- 0, 344788 = 0, 655212 =0, 655.
14) Для того, чтобы облегчить расчеты, можно с помощью пакета программ  выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:
выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:
Таблица 2.5- Расчетная таблица
Граница интервала 
| 
| 
| 
| 
|
| 0, 655212 | 26, 21 | |||
| 5, 634 | -1, 06483 | 0, 344788 | 0, 221096 | 8, 844 |
| 11, 058 | -2, 08996 | 0, 123692 | 0, 079318 | 3, 173 |
| 16, 482 | -3, 1151 | 0, 044374 | 0, 028455 | 1, 138 |
| 21, 906 | -4, 14023 | 0, 015919 | 0, 010208 | 0, 408 |
| 27, 33 | -5, 16537 | 0, 005711 | 0, 003662 | 0, 146 |
| 32, 754 | -6, 19051 | 0, 002049 | 0, 002049 | 0, 082 |

| - 
| - | - | |
| Итого | - | - |
Таблица 2.6 – Расчет c2 для случайной величины Х, распределенной по показательному закону
Границы интервалов

| Частоты эмпири-ческие 
| Вероят-ности

| Частоты теоретические 
| 
|
| [0; 5, 634) | 0, 655 | 26, 21 | 
| |
| [5, 634; 11, 058) | 0, 221 | 8, 844 | 
| |
| [11, 058; 16, 482) | 0, 079 | 3, 173 | 
| |
| [16, 482; 21, 906) | 0, 028 | 1, 138 | ||
| [21, 906; 27, 33) | 0, 01 | 0, 408 | ||
| [27, 33; 32, 754) | 0, 004 | 0, 146 | ||
[32, 754;  ) )
| 0, 002 | 0, 082 | ||
| Итого | 0, 863 = c2 |
15) Вычислим число степеней свободы n = k – r – 1 = 3-1-1= 1, где k = 3– число интервалов в таблице 2.6 после объединения, r =1 - число параметров выбранного закона распределения – в нашем случае показательный закон (один параметр  ).
).
16) По таблицам квантилей распределения c2 определяется критическое значение  =
=  = 3, 841 (Приложение Б), соответствующее заданному уровню значимости a=0, 05 и числу степеней свободы n = 1.
= 3, 841 (Приложение Б), соответствующее заданному уровню значимости a=0, 05 и числу степеней свободы n = 1.
Вывод. Так как расчетное  = 0, 863 меньше, чем табличное
= 0, 863 меньше, чем табличное  = 3, 841, то гипотеза о показательном законе распределения непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, подтвердилась.
= 3, 841, то гипотеза о показательном законе распределения непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, подтвердилась.
Порядок выполнения работы
1 Принять значение уровня значимости a.
2 Выдвинуть гипотезу о виде закона распределения изучаемой случайной величины по данным из лабораторной работы №1.
3 Проверить согласование сформулированной гипотезы с имеющимися выборочными данными (ручной расчёт):
– вычислить оценки параметров предполагаемого закона распределения;
– определить значения теоретических частот npi, i = 1, 2, …, k;
– вычислить выборочное значение критерия c2;
–сравнить выборочное значение критерия с критическим значением  и сделать вывод.
и сделать вывод.
4 Проверить согласование выдвинутой гипотезы с имеющимися экспериментальными данными с помощью ППП:
– вычислить выборочное значение критерия c2 (приложение А, п. 9);
– построить совместное графическое изображение статистического и предполагаемого теоретического распределений изучаемой случайной величины (см. приложение А, п. 9).
5 Сделать вывод о законе распределения вероятностей изучаемой случайной величины.
Контрольные вопросы
1 Что такое непараметрическая гипотеза?
2 Что такое нулевая, альтернативная гипотезы?
3 Из каких соображений выдвигается гипотеза о виде закона распределения случайной величины?
4 Что такое статистический критерий?
5 Какие ошибки могут быть совершены при статистической проверке гипотез?
6 Что такое уровень значимости статистического критерия?
7 Что называется статистическим критерием значимости?
8 По какой формуле вычисляется критерий c2?
9 Сформулируйте алгоритм применения критерия Пирсона.
10 Как найти критическое значение критерия  ?
?
11 Как вычислить число степеней свободы  ?
?
ПРИЛОЖЕНИЕ А (справочное) Таблица значений функции Лапласа

| х | Сотые доли х | |||||||||
| 0.0 | 0.0000 | |||||||||
| 0.1 | 0.0398 | |||||||||
| 0.2 | 0.0793 | |||||||||
| 0.3 | 0.1179 | |||||||||
| 0.4 | 0.1554 | |||||||||
| 0.5 | 0.1915 | |||||||||
| 0.6 | 0.2257 | |||||||||
| 0.7 | ||||||||||
| 0.8 | ||||||||||
| 0.9 | ||||||||||
| 1.0 | 0.3413 | |||||||||
| 1.1 | ||||||||||
| 1.2 | ||||||||||
| 1.3 | ||||||||||
| 1.4 | ||||||||||
| 1.5 | ||||||||||
| 1.6 | ||||||||||
| 1.7 | ||||||||||
| 1.8 | ||||||||||
| 1.9 | ||||||||||
| 2.0 | 0.4772 | |||||||||
| 2.1 | ||||||||||
| 2.2 | ||||||||||
| 2.3 | ||||||||||
| 2.4 | ||||||||||
| 2.5 | ||||||||||
| 2.6 | ||||||||||
| 2.7 | ||||||||||
| 2.8 | ||||||||||
| 2.9 | ||||||||||
| 3.0 | 0.49865 | |||||||||
| 3.1 | 0.49903 | |||||||||
| 3.2 | 0.49931 | |||||||||
| 3.3 | 0.49952 | |||||||||
| 3.4 | 0.49966 | |||||||||
| 3.6 | 0.499841 | |||||||||
| 3.8 | 0.499928 | |||||||||
| 4.0 | 0.499968 | |||||||||
| 4.5 | 0.499997 | |||||||||
| 5.0 | 0.4999997 | |||||||||

| 0.5 |
ПРИЛОЖЕНИЕ Б
(справочное)
Критические точки распределения c2
| Степени свободы n | Уровень значимости a | ||||||||
| 0.001 | 0.01 | 0.025 | 0.05 | 0.1 | 0.9 | 0.95 | 0.975 | 0.99 | |
| 10.827 | 6.635 | 5.024 | 3.841 | 2.706 | 0.016 | 0.0039 | 0.00098 | 0.00016 | |
| 13.815 | 9.210 | 7.378 | 5.991 | 4.605 | 0.211 | 0.103 | 0.051 | 0.020 | |
| 16.266 | 11.345 | 9.348 | 7.815 | 6.251 | 0.584 | 0.352 | 0.216 | 0.115 | |
| 18.466 | 13.277 | 11.143 | 9.488 | 7.779 | 1.064 | 0.711 | 0.484 | 0.297 | |
| 20.515 | 15.086 | 12.832 | 11.070 | 9.236 | 1.610 | 1.145 | 0.831 | 0.554 | |
| 22.457 | 16.812 | 14.449 | 12.592 | 10.645 | 2.204 | 1.635 | 1.237 | 0.872 | |
| 24.321 | 18.475 | 16.013 | 14.067 | 12.017 | 2.833 | 2.167 | 1.690 | 1.239 | |
| 26.124 | 20.090 | 17.535 | 15.507 | 13.362 | 3.490 | 2.733 | 2.180 | 1.647 | |
| 27.877 | 21.666 | 19.023 | 16.919 | 14.684 | 4.168 | 3.325 | 2.700 | 2.088 | |
| 29.588 | 23.209 | 20.483 | 18.307 | 15.987 | 4.865 | 3.940 | 3.247 | 2.558 | |
| 31.264 | 24.725 | 21.920 | 19.675 | 17.275 | 5.578 | 4.575 | 3.816 | 3.053 | |
| 32.909 | 26.217 | 23.337 | 21.026 | 18.549 | 6.304 | 5.226 | 4.404 | 3.571 | |
| 34.527 | 27.688 | 24.736 | 22.362 | 19.812 | 7.041 | 5.892 | 5.009 | 4.107 | |
| 36.124 | 29.141 | 26.119 | 23.685 | 21.064 | 7.790 | 6.571 | 5.629 | 4.660 | |
| 37.698 | 30.578 | 27.488 | 24.996 | 22.307 | 8.547 | 7.261 | 6.262 | 5.229 | |
| 39.252 | 32.000 | 28.845 | 26.296 | 23.542 | 9.312 | 7.962 | 6.908 | 5.812 | |
| 40.791 | 33.409 | 30.191 | 27.587 | 24.769 | 10.085 | 8.672 | 7.564 | 6.408 | |
| 42.312 | 34.805 | 31.526 | 28.869 | 25.989 | 10.865 | 9.390 | 8.231 | 7.015 | |
| 43.819 | 36.191 | 32.852 | 30.144 | 27.204 | 11.651 | 10.117 | 8.907 | 7.633 | |
| 45.314 | 37.566 | 34.170 | 31.410 | 28.412 | 12.443 | 10.851 | 9.591 | 8.260 | |
| 46.796 | 38.932 | 35.479 | 32.671 | 29.615 | 13.240 | 11.591 | 10.283 | 8.897 | |
| 48.268 | 40.289 | 36.781 | 33.924 | 30.813 | 14.041 | 12.338 | 10.982 | 9.542 | |
| 49.728 | 41.638 | 38.076 | 35.172 | 32.007 | 14.848 | 13.091 | 11.689 | 10.196 | |
| 51.179 | 42.980 | 39.364 | 36.415 | 33.196 | 15.659 | 13.848 | 12.401 | 10.856 | |
| 52.619 | 44.314 | 40.646 | 37.652 | 34.382 | 16.473 | 14.611 | 13.120 | 11.524 | |
| 54.051 | 45.642 | 41.923 | 38.885 | 35.563 | 17.292 | 15.379 | 13.844 | 12.198 | |
| 55.475 | 46.963 | 43.195 | 40.113 | 36.741 | 18.114 | 16.151 | 14.573 | 12.878 | |
| 56.892 | 48.278 | 44.461 | 41.337 | 37.916 | 18.939 | 16.928 | 15.308 | 13.565 | |
| 58.301 | 49.588 | 45.722 | 42.557 | 39.087 | 19.768 | 17.708 | 16.047 | 14.256 | |
| 59.702 | 50.892 | 46.979 | 43.773 | 40.256 | 20.599 | 18.493 | 16.791 | 14.953 | |
| 61.098 | 52.191 | 48.232 | 44.985 | 41.422 | 21.434 | 19.281 | 17.539 | 15.655 | |
| 62.487 | 53.486 | 49.480 | 46.194 | 42.585 | 22.271 | 20.072 | 18.291 | 16.362 | |
| 63.869 | 54.775 | 50.725 | 47.400 | 43.745 | 23.110 | 20.867 | 19.047 | 17.073 | |
| 65.247 | 56.061 | 51.966 | 48.602 | 44.903 | 23.952 | 21.664 | 19.806 | 17.789 | |
| 66.619 | 57.342 | 53.203 | 49.802 | 46.059 | 24.797 | 22.465 | 20.569 | 18.509 | |
| 67.985 | 58.619 | 54.437 | 50.998 | 47.212 | 25.643 | 23.269 | 21.336 | 19.233 | |
| 69.348 | 59.893 | 55.668 | 52.192 | 48.363 | 26.492 | 24.075 | 22.106 | 19.960 | |
| 70.704 | 61.162 | 56.895 | 53.384 | 49.513 | 27.343 | 24.884 | 22.878 | 20.691 | |
| 72.055 | 62.428 | 58.120 | 54.572 | 50.660 | 28.196 | 25.695 | 23.654 | 21.426 | |
| 73.403 | 63.691 | 59.342 | 55.758 | 51.805 | 29.051 | 26.509 | 24.433 | 22.164 |
|