
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двух нормально распределенных генеральных
|
|
Проверка гипотезы о равенстве дисперсий
совокупностей (выборки независимые)
Задача проверки гипотезы о равенстве двух дисперсий на практике возникает довольно часто. Например, при анализе стабильности производственного процесса до и после введения технических усовершенствований (сравнивается колеблемость в выпуске продукции); при изучении точности измерительных приборов, инструментов, машин; при изучении степени однородности двух совокупностей в отношении какого-либо признака, например стажа рабочих; при сравнении рисков, связанных с отклонением доходности акций от ожидаемого уровня и т.д.
Пусть даны две генеральные совокупности Х и Y, которые имеют нормальный закон распределения. Есть основание предположить, что их генеральные дисперсии равны, то есть выдвинуть нулевую гипотезу Н 0: D (Х) = D (Y). Проверим эту гипотезу при заданном уровне значимости  .
.
Для этого проведем независимые выборки из этих данных генеральных совокупностей с объемами, соответственно, равными nx и ny. По данным выборок находим оценки генеральных дисперсий - исправленные выборочные дисперсии  ,
,  , которые будут несмещенными оценками, то есть
, которые будут несмещенными оценками, то есть 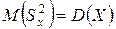 и
и  . Тогда нулевую гипотезу можно записать и так: Н 0:
. Тогда нулевую гипотезу можно записать и так: Н 0: 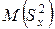 =
=  .
.
Практически же исправленные дисперсии, как правило, будут различаться. Наша задача выявить существенно (значимо) или несущественно (незначимо) это различие, так как:
1) если нулевая гипотеза справедлива, то есть D (Х) = D (Y), то различие исправленных дисперсий случайное (незначимо), например, за счет случайного отбора элементов выборок;
2) если нулевая гипотеза отвергнута, то различие исправленных дисперсий существенное (значимо), оно является следствием того, что генеральные дисперсии различны.
Итак, необходимо выявить значимость различия исправленных дисперсий. Воспользуемся случайной величиной 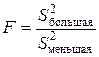 .
.
Покажем, что случайная величина F имеет распределение Фишера - Снедекора, если нормально распределенные признаки Х и Y имеют равные дисперсии. Примем для определенности, что  является оценкой
является оценкой  , а
, а 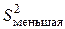 - оценкой
- оценкой  .
.
Тогда  .
.
Следовательно, если  , то случайная величина F имеет распределение Фишера - Снедекора
, то случайная величина F имеет распределение Фишера - Снедекора 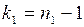 и
и  степенями свободы. Здесь n 1 - объем выборки, по которой рассчитана
степенями свободы. Здесь n 1 - объем выборки, по которой рассчитана  , n 2 - соответственно,
, n 2 - соответственно,  .
.
По выборочным данным находят  . Далее нужно найти критическую точку F крит и критическую область, которая строится в зависимости от вида конкурирующей гипотезы.
. Далее нужно найти критическую точку F крит и критическую область, которая строится в зависимости от вида конкурирующей гипотезы.
Чаще всего выбирают конкурирующую гипотезу следующего вида:
Н 1: D (Х) > D (Y).
Эта конкурирующая гипотеза определяет правостороннюю критическую область  , которая строится, исходя из требования
, которая строится, исходя из требования  (F > F крит (a, k1, k2))=
(F > F крит (a, k1, k2))=  (здесь F крит (a, k1, k2) = F крит. пр (a, k1, k2)).
(здесь F крит (a, k1, k2) = F крит. пр (a, k1, k2)).

Рис. 1
Критическую точку F крит(a, k 1, k 2) можно найти по таблице критических точек распределения Фишера - Снедекора (см. прил. 6 файла «Приложения»). Далее сравниваем наблюдаемое и критическое значение критерия и делаем вывод.
При формулировке вывода руководствуются следующим правилом: если наблюдаемое значение критерия F набл попало в область принятия гипотезы (F набл < F крит(a, k 1, k 2)) (рис. 1), то нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), и расхождение между исправленными выборочными дисперсиями случайное; если же наблюдаемое значение критерия F набл попало в критическую область (F набл > F крит(a, k 1, k 2)), то нулевая гипотеза отвергается, а принимается конкурирующая гипотеза D (Х) > D (Y), то есть расхождение между исправленными выборочными дисперсиями значимо.
Замечание. При проверке гипотезы о равенстве генеральных дисперсий при заданном уровне значимости a контролируется лишь ошибка первого рода, но нельзя ничего сказать о степени риска, связанного с принятием неверной гипотезы 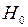 , то есть с возможностью ошибки второго рода.
, то есть с возможностью ошибки второго рода.
Пример 1. По двум независимым выборкам, объемы которых nx = 9 и ny = 16, извлеченным из нормально распределенных генеральных совокупностей Х и Y, найдены исправленные выборочные дисперсии 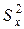 = 34, 02 и
= 34, 02 и  = 12, 15. При уровне значимости 0, 01 проверить гипотезу о равенстве генеральных дисперсий.
= 12, 15. При уровне значимости 0, 01 проверить гипотезу о равенстве генеральных дисперсий.
Решение. Совокупности Х и Y имеют нормальный закон распределения. Выдвигаем гипотезы:
Н 0: D (Х) = D (Y),
Н 1: D (Х) > D (Y).
Проверяется нулевая гипотеза по выборочным данным. С этой целью сделаны выборки объемами nx = 9, ny = 16 и найдены точечные оценки генеральных дисперсий: 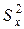 = 34, 02 и
= 34, 02 и  = 12, 15.
= 12, 15.
Гипотеза проверяется с помощью случайной величины 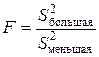 , которая имеет распределение Фишера - Снедекора с k 1 = nх - 1 = 8 и k 2 = ny - 1 = 15 степенями свободы. Находим
, которая имеет распределение Фишера - Снедекора с k 1 = nх - 1 = 8 и k 2 = ny - 1 = 15 степенями свободы. Находим  . По таблице критических точек распределения Фишера - Снедекора (прил. 6) находим F крит(0, 01; 8; 15) = 4, 0. Сравниваем F набл и F крит(0, 01; 8; 15). Так как F набл < F крит(0, 01; 8; 15), то есть F набл попало в область принятия гипотезы (рис. 2), то нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), а расхождение между исправленными выборочными дисперсиями случайное.
. По таблице критических точек распределения Фишера - Снедекора (прил. 6) находим F крит(0, 01; 8; 15) = 4, 0. Сравниваем F набл и F крит(0, 01; 8; 15). Так как F набл < F крит(0, 01; 8; 15), то есть F набл попало в область принятия гипотезы (рис. 2), то нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), а расхождение между исправленными выборочными дисперсиями случайное.
Пример 2. Для сравнения точности двух станков-автоматов взяты две пробы (выборки), объемы которых n 1 = 10 и n 2 = 8. В результате измерений контролируемого размера отобранных изделий получены следующие результаты:
xi: 1, 08; 1, 10; 1, 12; 1, 14; 1, 15; 1, 25; 1, 36; 1, 38; 1, 40; 1, 42;
yj: 1, 11; 1, 12; 1, 18; 1, 22; 1, 33; 1, 35; 1, 36; 1, 38.
Можно ли считать, что станки обладают одинаковой точностью при уровне значимости 0, 05?
Решение. Признак Х - размер изделия, обработанного на первом станке-автомате. Признак Y - размер изделия, обработанного на втором станке-автомате. Пусть признаки имеют нормальный закон распределения. Выдвигаем гипотезы:
Н 0: D (Х) = D (Y),
Н 1: D (Х) > D (Y).
Проверим нулевую гипотезу по выборочным данным с помощью случайной величины 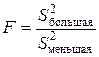 , которая имеет распределение Фишера - Снедекора с
, которая имеет распределение Фишера - Снедекора с  и
и  степенями свободы, где n 1 - объем выборки, по которой найдена
степенями свободы, где n 1 - объем выборки, по которой найдена  .
.
Предварительно по выборочным данным вычислим исправленные выборочные дисперсии исследуемых признаков. Расчеты представим в таблице:
| xi | xi 2 | yj | yj 2 | |
| 1, 08 1, 10 1, 12 1, 14 1, 15 1, 25 1, 36 1, 38 1, 40 1, 42 | 1, 1664 1, 21 1, 2544 1, 2996 1, 3225 1, 5625 1, 8496 1, 9044 1, 96 2, 0164 | 1, 11 1, 12 1, 18 1, 22 1, 33 1, 35 1, 36 1, 38 - - | 1, 2321 1, 2544 1, 3924 1, 4884 1, 7689 1, 8225 1, 8496 1, 9044 - - | |
| Итого | 12, 4 | 15, 5458 | 10, 05 | 12, 7127 |



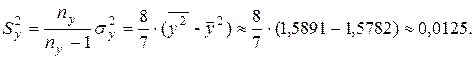
Найдем наблюдаемое значение критерия:
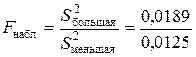 »1, 51.
»1, 51.
По таблице критических точек распределения Фишера - Снедекора (прил. 6) находим F крит(a, k 1, k 2) = F крит(0, 05; 9, 7) = 3, 68. Сравниваем F набл и F крит(0, 05; 9; 7).
Так как F набл < F крит(0, 05; 9; 7), то есть наблюдаемое значение критерия попало в область принятия гипотезы (рис. 2), нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), расхождение между исправленными выборочными дисперсиями случайное. Следовательно, по данным наблюдения станки обладают одинаковой точностью.