Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия с матрицами
|
|
Тема 2. Начальные сведения о матрицах.
Прямоугольной матрицей размера т ´ п называется система чисел, расположенных виде таблицы
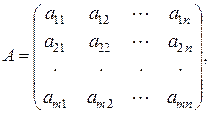
состоящей из т строк и п столбцов. Кратко матрицу А записывают виде 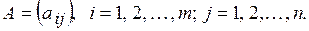 Числа
Числа  , составляющие данную матрицу, называют ее элементами. Первый индекс у элемента указывает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент.
, составляющие данную матрицу, называют ее элементами. Первый индекс у элемента указывает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент.
Матрицу называют комплексной, если хотя бы один ее элемент является комплексным числом, и действительной (вещественной), если все ее элементы – действительные (вещественные) числа.
Две матрицы одинакового размера т ´ п считаются равными, если равны их соответствующие элементы, т.е. элементы, стоящие на одинаковых местах в этих матрицах. Таким образом, одно равенство между матрицами размера т ´ п равносильно системе тп равенств между из элементами.
Матрицу, состоящую из одной строки или одного столбца, называют соответственно вектор-строкой или вектор-столбцом
 .
.
Элементы векторов называют их компонентами. Матрица, состоящая из одного числа, отождествляется с этим числом.
Матрица, состоящая из нулей, называется нулевой и обозначается 0.
Если число т строк матрицы равно числу п ее столбцов, то матрицу называют квадратной порядкап. Диагональ квадратной матрицы, соединяющая левый верхний угол с правым нижним, называют главной. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называют диагональными.
Диагональная матрица, у которой все элементы по главной диагонали одинаковые, называют скалярной. Частным случаем скалярных матриц является единичная матрица
 .
.
Матрицу, полученную из данной матрицы А заменой в ней строк на соответствующие столбцы, называют транспонированной А и обозначают через  или
или  . Если А – (т ´ п)-матрица, то
. Если А – (т ´ п)-матрица, то  – (п ´ т)-матрица, например,
– (п ´ т)-матрица, например,
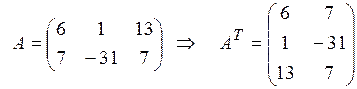 .
.
В частности, если А – вектор-строка, то  – вектор-столбец, и наоборот.
– вектор-столбец, и наоборот.
Матрицу А называют симметрической, если А =  , или другими словами
, или другими словами  , например
, например

Если же  = – А, то матрицу А называется кососимметрической. Элементы, расположенные симметрично относительно главной диагонали, у симметрической матрицы равны, а у кососимметрической противоположны. В частности, все диагональные элементы кососимметрической матрицы равны нулю. Пример кососимметрической матрицы
= – А, то матрицу А называется кососимметрической. Элементы, расположенные симметрично относительно главной диагонали, у симметрической матрицы равны, а у кососимметрической противоположны. В частности, все диагональные элементы кососимметрической матрицы равны нулю. Пример кососимметрической матрицы
 .
.
Матрицу  называют комплексно сопряженной к матрице А, если она получена из А заменой в ней элементов на комплексно сопряженные; матрицу
называют комплексно сопряженной к матрице А, если она получена из А заменой в ней элементов на комплексно сопряженные; матрицу  – эрмитово-сопряженной, или сопряженной к матрице А, если она получена из А заменой в ней элементов на комплексно сопряженные и транспонированием, т.е.
– эрмитово-сопряженной, или сопряженной к матрице А, если она получена из А заменой в ней элементов на комплексно сопряженные и транспонированием, т.е.  . Для действительной матрицы
. Для действительной матрицы  .
.
Квадратная матрица называется эрмитовой, если 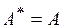 , например
, например
 .
.

Суммой матриц  и
и  одинакового размера т ´ п называется матрица
одинакового размера т ´ п называется матрица  того же размера, элементы которой равны суммам
того же размера, элементы которой равны суммам 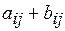 соответствующих элементов слагаемых матриц. Таким образом,
соответствующих элементов слагаемых матриц. Таким образом,
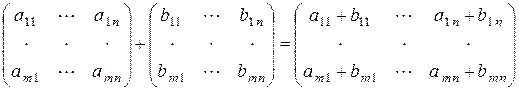 Разность матриц определяется аналогично.
Разность матриц определяется аналогично.
Произведение матрицы  на число a называют матрицу aА, все элементы которой равны произведениям соответствующих элементов исходной матрицы на это число:
на число a называют матрицу aА, все элементы которой равны произведениям соответствующих элементов исходной матрицы на это число:
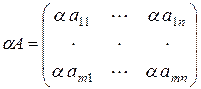 .
.
В частности, матрицу (–1) А называют противоположной матрице А и обозначают – А.
Линейной комбинацией вектор-строк (столбцов) одинакового размера 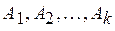 называют вектор-стоку (столбец)
называют вектор-стоку (столбец)

Например,

Сложение матриц и умножение их на числа обладают следующими свойствами при любых матрицах А, В, С и любых a, b:
1) А + В = В + А
(коммутативность),
2) А + (В + С) = (А + В) + С
(ассоциативность)
3) А + 0 = А, (существование
нулевого элемента)
4) А + (– А) = 0, (существование противоположного элемента)
5) 1 × А = А,
6) (a + b) × А = a А + b А,
7) a × (А + В) = a А + a В,
8) a × (b А) = (ab)× А
Умножение матриц определяется лишь для случая, когда число столбцов первого сомножителя равно числу строк второго сомножителя.
Пусть

Произведение матриц А и В, заданных в указанном порядке, называется матрица  , элементы которой определяются по следующему правилу:
, элементы которой определяются по следующему правилу:

т.е. элемент 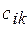 матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы k -го столбца матрицы В. Из этого определения следует, что матрица С будет матрицей размера т ´ р. Произведение двух матриц зависит от порядка сомножителей (!), т.е. произведение матриц не обладает свойством коммутативности.
матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы k -го столбца матрицы В. Из этого определения следует, что матрица С будет матрицей размера т ´ р. Произведение двух матриц зависит от порядка сомножителей (!), т.е. произведение матриц не обладает свойством коммутативности.
Например, даны матрицы
 . Найдем произведения АВ и ВА.
. Найдем произведения АВ и ВА.

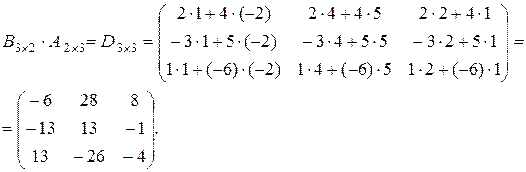
Если рассматривать матрицы не квадратные, то может случиться даже, что произведение матриц в одном порядке будет иметь смысл, а в обратном – нет. Например, произведение АВ матриц  и
и  существует, а произведение ВА не существует.
существует, а произведение ВА не существует.
Умножение матриц обладает следующими свойствами:
1) А (ВС) = (АВ) С (ассоциативность),
2) a (АВ) = (aА) В = А (aВ),
3) С (А + В) = СА + СВ (левая дистрибутивность),
4) (А+В) С = АС + ВС (правая дистрибутивность).
К особенностям умножения матриц можно отнести существование делителей нуля, т.е. из условия АВ = О не следует, что А = О или В = О. Например, если возьмем ненулевые матрицы  и
и  , то результатом их произведения будет нулевая матрица (АВ = О).
, то результатом их произведения будет нулевая матрица (АВ = О).
Рассмотрим некоторые свойства операций транспонирования и комплексного сопряжения матриц:
1) 
2) 
3) 
4) 
5) 
Матрицы А и В называются перестановочными, если АВ = ВА.
Рассмотрим произвольную квадратную матрицу Х порядка п. По определению полагаем

Все натуральные степени одной и той же матрицы перестановочны между собой, т.е.  .
.
Рассмотрим теперь какой-нибудь многочлен

от буквы х, коэффициенты которого некоторые числа. Если А – некоторая квадратная матрица, то выражение

называют значением многочлена f (x) при х = А или соответствующим многочленом от матрицы А.
Например, найдем f (A), если  при условии, что
при условии, что 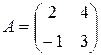 .
.
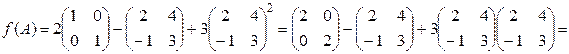
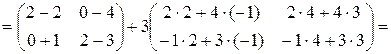

Разобьем какую-нибудь матрицу А системой вертикальных и горизонтальных прямых на части. Эти части можно рассматривать как матрицы низших порядков, из которых сама матрица построена как из элементов. Они называются клетками или блоками матрицы А, а сама матрица А, разбитая определенным образом на клетки, называется соответственно клеточной или блочной. Одна и та же матрица может быть разбита на клетки различными способами, например

Клеточная матрица вида

где  квадратные клетки, а О – нулевые матрицы надлежащих размерностей, называется клеточно-диагоналиной. Вместо этого говорят также, что А распадается на части
квадратные клетки, а О – нулевые матрицы надлежащих размерностей, называется клеточно-диагоналиной. Вместо этого говорят также, что А распадается на части  или что А есть прямая сумма матриц
или что А есть прямая сумма матриц 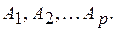
Операции над распавшимися матрицами приводятся к операциям над их диагональными клетками. Отсюда в свою очередь следует, что если f (x) – некоторый многочлен и А – клеточно-диагональная матрица с диагональными клетками  то
то
 .
.
Рассмотрим пример: зная матрицу А, найдем А 2.