
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Существует пять правильных многогранников.
|
|
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ».
Определение. Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани - равные друг другу правильные многоугольники; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные углы равны.
По теореме Эйлера для любого многогранника, имеющего В вершин, Р ребер и Г граней, выполняется соотношение: В - Р + Г = 2.
Пусть каждая грань многогранника имеет m ребер, и в каждой вершине многогранника сходятся n ребер. Очевидно, что 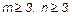
Так как у многогранника В вершин, и в каждой вершине сходятся n ребер, то получится n× В ребер. Но любое ребро соединяет две вершины многогранника, поэтому в произведение n× В каждое ребро войдет дважды. Значит, у многогранника имеется 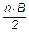 различных ребер. Тогда
различных ребер. Тогда 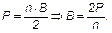
В каждой грани многогранника m ребер, а число граней равно Г. Так как каждое ребро принадлежит двум различным граням, то число различных ребер многогранника равно 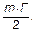 Тогда
Тогда 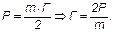
Получим 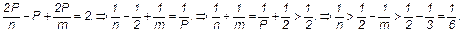
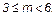 Аналогично
Аналогично 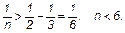
Гранями правильного многогранника могут быть либо правильные треугольники, либо правильные четырехугольники (квадраты), либо правильные пятиугольники. Количество ребер, сходящихся в одной вершине, меньше 6.
1) При n = 3 и m = 3 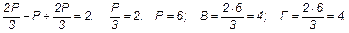
2) При n = 4 и m = 3 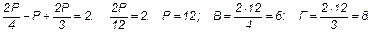
3) При n = 5 и m = 3 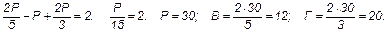
4) При n = 3 и m = 4 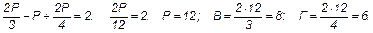
5) При n = 4 и m = 4 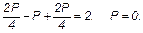
6) При n = 5 и m = 4 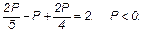
4) При n = 3 и m = 5 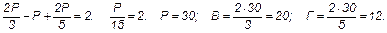
5) При n = 4 и m = 5 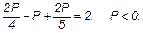
6) При n = 5 и m = 5 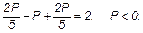
Существует пять правильных многогранников.
| Название многогранника | Вид грани | В | Р | Г |
| Правильный тетраэдр | Правильный треугольник | |||
| Правильный октаэдр | Правильный треугольник | |||
| Правильный икосаэдр | Правильный треугольник | |||
| Правильный гексаэдр (куб) | Квадрат | |||
| Правильный додекаэдр | Правильный пятиугольник |
|