Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № 8
|
|
“Определенный интеграл и его приложения”
ЗАДАНИЕ 1. Вычислить интегралы:
| 1. | 1) 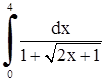 ;
2) ;
2) 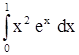 . .
| 2. | 1)  ;
2) ;
2) 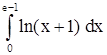 . .
| 3. | 1) 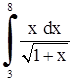 ;
2) ;
2) 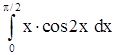 . .
|
| 4. | 1)  ;
2) ;
2) 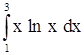 . .
| 5. | 1) 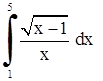 ;
2) ;
2) 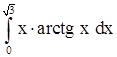 . .
| 6. | 1) 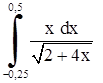 ;
2) ;
2) 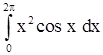 . .
|
| 7. | 1) 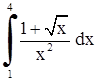 ;
2) ;
2) 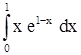 . .
| 8. | 1) 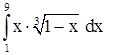 ;
2) ;
2) 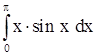 . .
| 9. | 1) 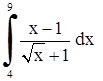 ;
2) ;
2) 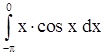 . .
|
| 10. | 1) 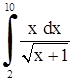 ;
2) ;
2) 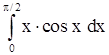 . .
| 11. | 1) 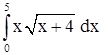 ;
2) ;
2)  . .
| 12. | 1) 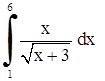 ;
2) ;
2) 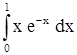 . .
|
| 13. | 1) 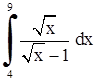 ;
2) ;
2)  . .
| 14. | 1) 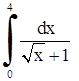 ;
2) ;
2) 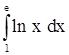 . .
| 15. | 1) 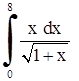 ;
2) ;
2) 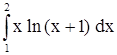 . .
|
| 16. | 1) 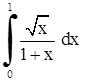 ;
2) ;
2) 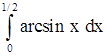 . .
| 17. | 1) 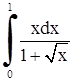 ;
2) ;
2) 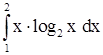 . .
| 18. | 1) 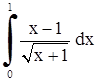 ;
2) ;
2) 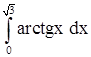 . .
|
| 19. | 1) 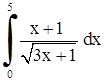 ;
2) ;
2) 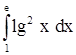 . .
| 20. | 1) 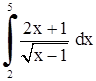 ;
2) ;
2) 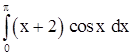 . .
| 21. | 1) 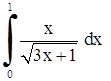 ;
2) ;
2) 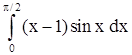 . .
|
| 22. | 1)  ;
2) ;
2) 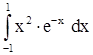 . .
| 23. | 1) 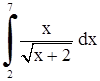 ;
2) ;
2) 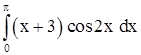 . .
| 24. | 1) 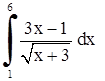 ;
2) ;
2) 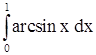 . .
|
| 25. | 1) 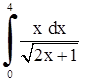 ;
2) ;
2) 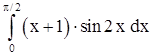 . .
| 26. | 1)  ;
2) ;
2) 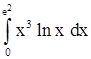 . .
| 27. | 1) 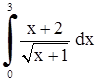 ;
2) ;
2) 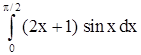 . .
|
| 28. | 1) 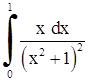 ;
2) ;
2) 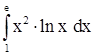 . .
| 29. | 1) 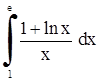 ;
2) ;
2) 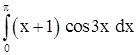 . .
| 30. | 1)  ;
2) ;
2)  . .
|
ЗАДАНИЕ 2. Вычислить площади фигур, ограниченных линиями:
| 1. | 1) 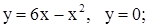
| 2) 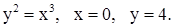
| ||
| 2. | 1) 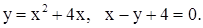
| 2) 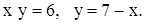
| ||
| 3. | 1) 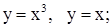
| 2) 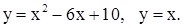
| ||
| 4. | 1) 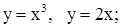
| 2) 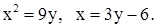
| ||
| 5. | 1) 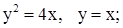
| 2) 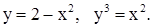
| ||
| 6. | 1) 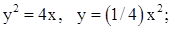
| 2) 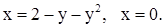
| ||
| 7. | 1) 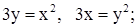
| 2) 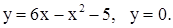
| ||
| 8. | 1) 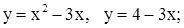
| 2) 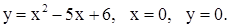
| ||
| 9. | 1) 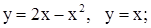
| 2) 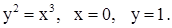
| ||
| 10. | 1) 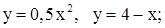
| 2) 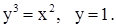
| ||
| 11. | 1) 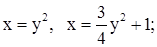
| 2) 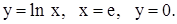
| ||
| 12. | 1) 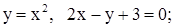
| 2) 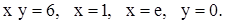
| ||
| 13. | 1) 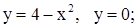
| 2) 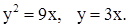
| ||
| 14. | 1) 
| 2) 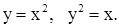
| ||
| 15. | 1) 
| 2) 
| ||
| 16. | 1) 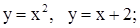
| 2) 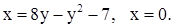
| ||
| 17. | 1) 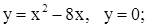
| 2) 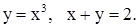
| ||
| 18. | 1) 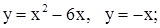
| 2) 
| ||
| 19. | 1) 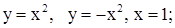
| 2) 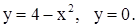
| ||
| 20. | 1) 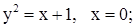
| 2) 
| ||
| 21. | 1) 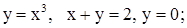
| 2) 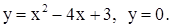
| ||
| 22. | 1) 
| 2) 
| ||
| 23. | 1) 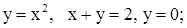
| 2) 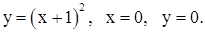
| ||
| 24. | 1) 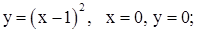
| 2) 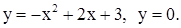
| ||
| 25. | 1) 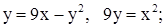
| 2) 
| ||
| 26. | 1) 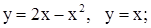
| 2) 
| ||
| 27. | 1) 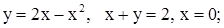
| 2) 
| ||
| 28. | 1) 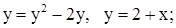
| 2) 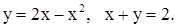
| ||
| 29. | 1) 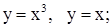
| 2) 
| ||
| 30. | 1) 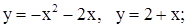
| 2) 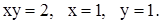
| ||
ЗАДАНИЕ 3. Найти объемы тел, образованных вращением вокруг оси  фигуры, ограниченной линиями:
фигуры, ограниченной линиями:
| 1. | 1) 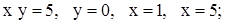
| 2) 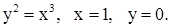
| |||
| 2. | 1) 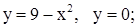
| 2) 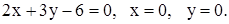
| |||
| 3. | 1) 
| 2) 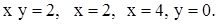
| |||
| 4. | 1) 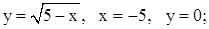
| 2) 
| |||
| 5. | 1) 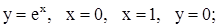
| 2) 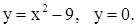
| |||
| 6. | 1) 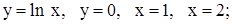
| 2) 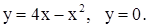
| |||
| 7. | 1) 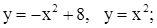
| 2) 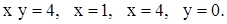
| |||
| 8. | 1) 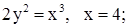
| 2) 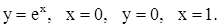
| |||
| 9. | 1) 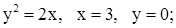
| 2) 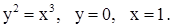
| |||
| 10. | 1) 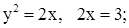
| 2) 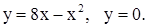
| |||
| 11. | 1) 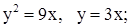
| 2) 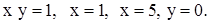
| |||
| 12. | 1) 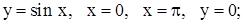
| 2) 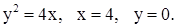
| |||
| 13. | 1) 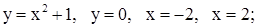
| 2) 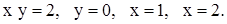
| |||
| 14. | 1) 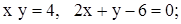
| 2) 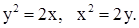
| |||
| 15. | 1) 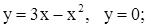
| 2) 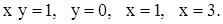
| |||
| 16. | 1) 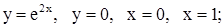
| 2) 
| |||
| 17. | 1) 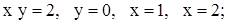
| 2) 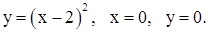
| |||
| 18. | 1) 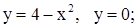
| 2) 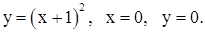
| |||
| 19. | 1) 
| 2) 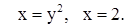
| |||
| 20. | 1) 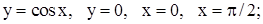
| 2) 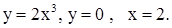
| |||
| 21. | 1) 
| 2) 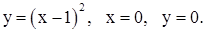
| |||
| 22. | 1) 
| 2) 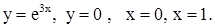
| |||
| 23. | 1) 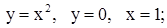
| 2) 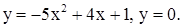
| |||
| 24. | 1) 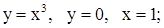
| 2) 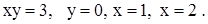
| |||
| 25. | 1) 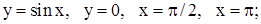
| 2) 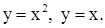
| |||
| 26. | 1) 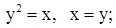
| 2) 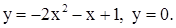
| |||
| 27. | 1) 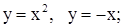
| 2) 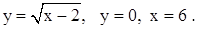
| |||
| 28. | 1) 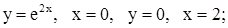
| 2) 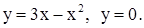
| |||
| 29. | 1) 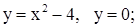
| 2) 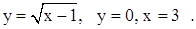
| |||
| 30. | 1) 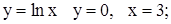
| 2) 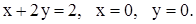
| |||
Образец выполнения контрольной работы № 8
“ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ”
1) Вычислить интегралы.
а) 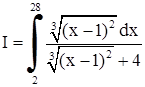 . Чтобы избавиться от кубического корня, заменим
. Чтобы избавиться от кубического корня, заменим
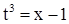 , тогда
, тогда 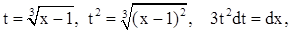 заменим пределы интегрирования
заменим пределы интегрирования 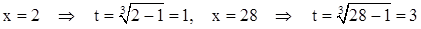 .
.
После подстановок получим
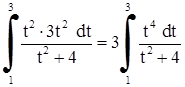 .
.
Под знаком интеграла неправильная рациональная дробь. Делим столбиком.




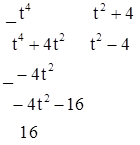
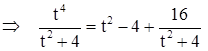 .
.
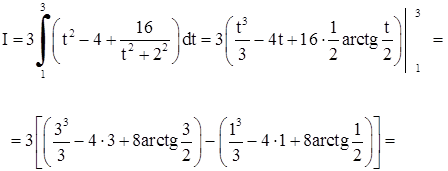
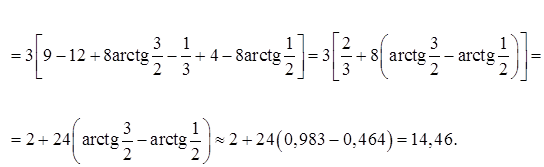
Ответ: 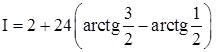 .
.
б). Интеграл 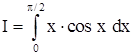 находим по частям с помощью подстановок:
находим по частям с помощью подстановок:
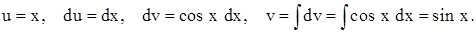
После преобразований получим
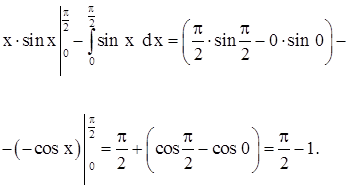
Ответ: 
|
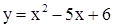 и прямой
и прямой 
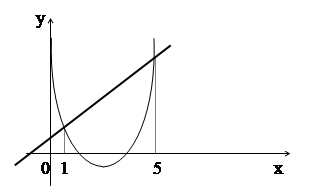
Рисунок 8
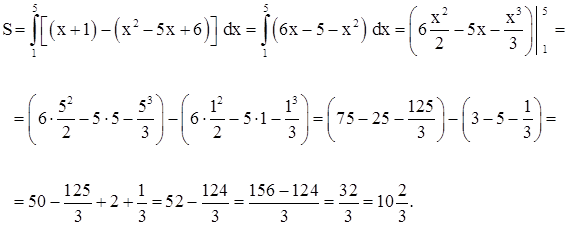
Ответ: 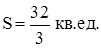
3) Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 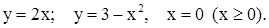
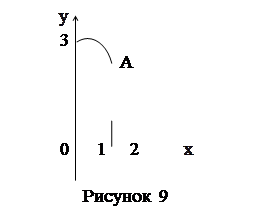 |
|



Выбираем, как дано, 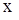 больше нуля, значит,
больше нуля, значит, 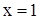 . Так как объем тела вращения
. Так как объем тела вращения 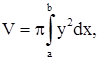 а в данном случае
а в данном случае 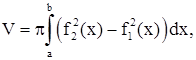 объем
объем
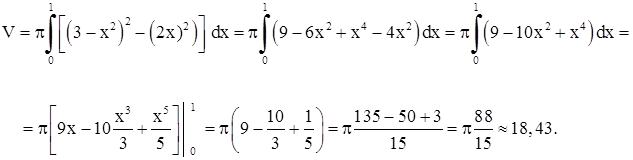
Ответ: 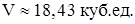
|
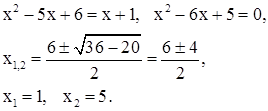 Так как
Так как 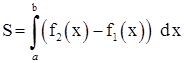 , то
площадь данной фигуры
, то
площадь данной фигуры
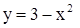 и прямой
и прямой 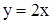 (рис. 9).
(рис. 9).