
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрия. Действия со степенями
|
|
Арифметика и алгебра
Действия со степенями
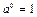
|
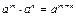
| 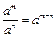
| 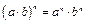
| 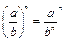
| 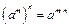
| ||
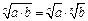
| 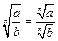
| 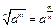
| 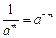
| 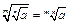
| 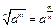
| ||
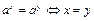
| 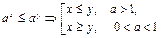
| 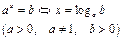
| |||||
Формулы сокращенного умножения
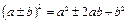
| 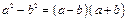
|
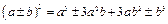
| 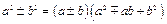
|
Корни квадратного уравнения 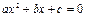
| По формуле Кардано | По теореме Виета |
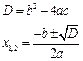
| 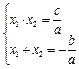
|
Разложение квадратного трехчлена на множители 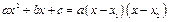
Выделение полного квадрата в квадратном трехчлене 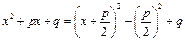
Арифметическая прогрессия
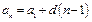
| 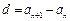
| 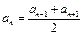
| 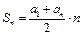
|
Геометрическая прогрессия
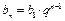
| 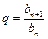
| 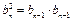
| 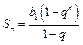 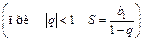
|
Логарифмы
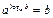
| 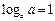
| 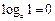
| 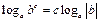
| 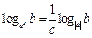
| 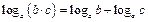
| ||||
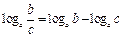
| 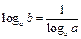
| 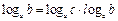
| 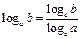
| 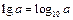
| 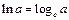
| ||||
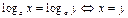
| 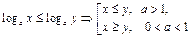
| 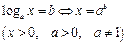
| |||||||
Тригонометрия
Основные соотношения
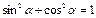
| 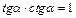
| 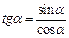
| 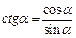
| 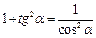
| 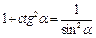
|
Сумма и разность двух аргументов Четность/ нечетность
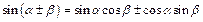
| 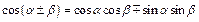
|
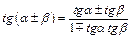
| 
|
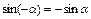
| 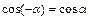
|
Двойные аргументы
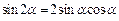
| 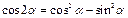
| 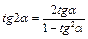
| 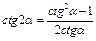
|
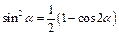
| 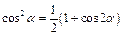
|
Формулы понижения степени
Преобразование произведения в сумму
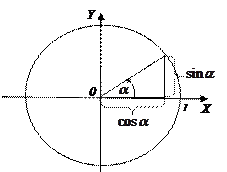
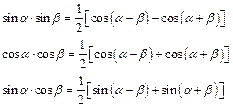
Преобразование суммы и разности в произведение
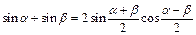
| 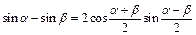
|
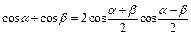
| 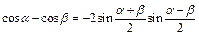
|
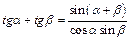
| 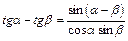
|
Тригонометрические уравнения
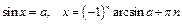
| 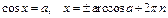
|
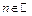
|
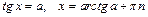
| 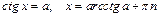
|
Основные значения 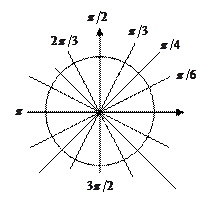

| 
| 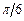
| 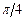
| 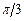
| 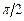
|
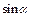
| 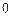
| 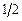
| 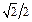
| 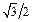
| 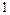
|
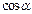
| 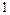
| 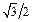
| 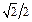
| 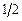
| 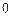
|
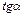
| 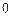
| 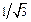
| 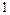
| 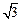
| 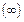
|
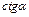
| 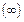
| 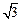
| 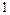
| 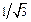
| 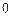
|

| 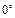
| 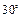
| 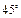
| 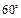
| 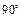
|
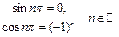
|

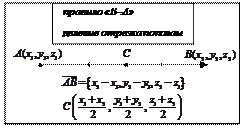



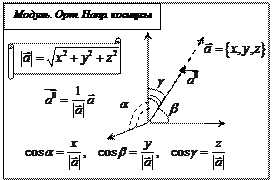 |
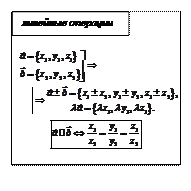
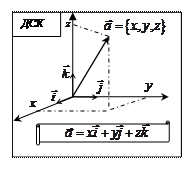
| Скалярное произведение (ЧИСЛО) | Векторное произведение (ВЕКТОР) | Смешанное произведение (ЧИСЛО) | ||||||
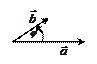 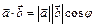
| 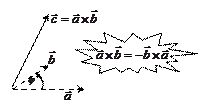
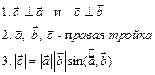 . .
| 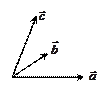
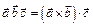
|
Производные некоторых элементарных функций
| 1. | 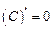
| 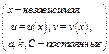
| 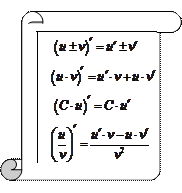
|
| 2. | 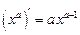 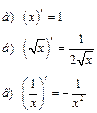
| 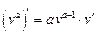

| |
| 3. | 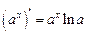 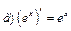 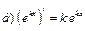
| 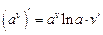 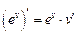
| |
| 4. | 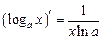 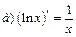
| 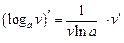 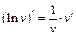
| |
| 5. | 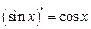 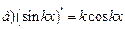
| 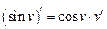
| |
| 6. | 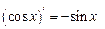 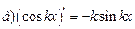
| 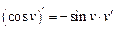
| |
| 7. | 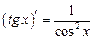
| 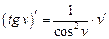
| |
| 8. | 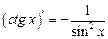
| 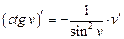
| |
| 9. | 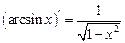
| 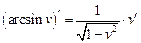
| |
| 10. | 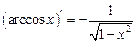
| 
| |
| 11. | 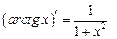
| 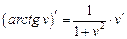
| |
| 12. | 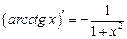
| 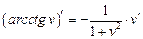
|
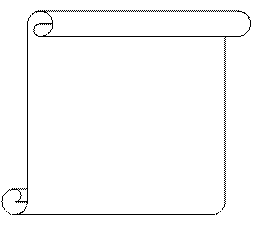
Интегралы некоторых функций
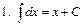
| 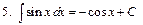 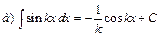
| 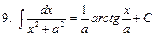 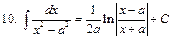
| |
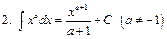 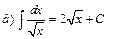 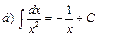
| |||
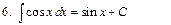 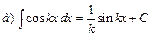
| 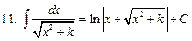 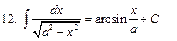
| ||
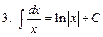
| 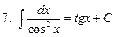 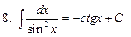
| 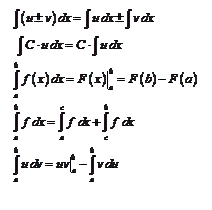 
| |
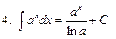 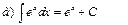 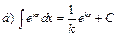
| |||
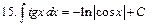 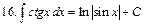
| |||
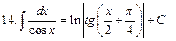 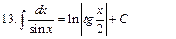
| |||
ОДУ 1-го порядка 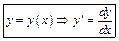
| ДУ с разделенными переменными | Однородные ДУ | Линейные (Бернулли) |
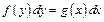
| 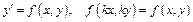
| 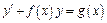
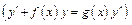
|
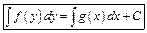
| 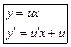
| 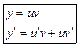
|
ОДУ высших порядков
1. Допускающие понижение порядка
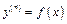
| 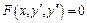
| 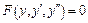
|
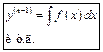
| 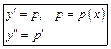
| 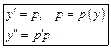
|
2. Линейные ДУ с постоянными коэффициентами
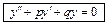 Общее решение
Общее решение 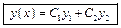 . Как найти . Как найти 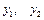 ? ?
Составляем характеристическое уравнение
| ||||||||||||||||||
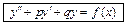 Общее решение
Общее решение 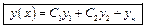 Здесь Здесь 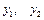 – см. выше. Как найти – см. выше. Как найти 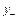 ? ?
Здесь |
Разложения в степенной ряд некоторых функций
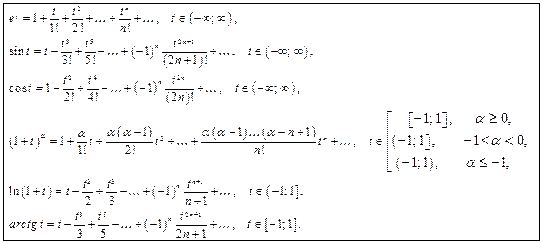
|
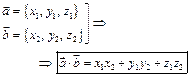
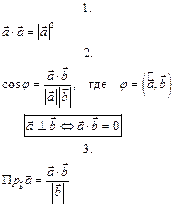
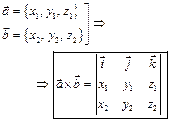
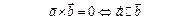
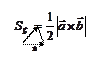 2.
2.
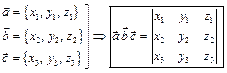
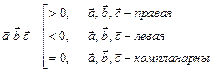 2.
2.
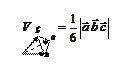
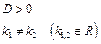
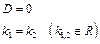
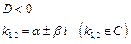
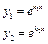
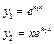
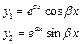
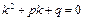 . Находим его корни по формуле
. Находим его корни по формуле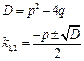 . Возможны следующие случаи
. Возможны следующие случаи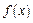
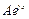
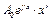
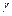
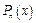
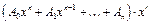
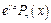
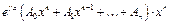
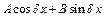
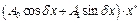
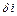
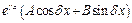
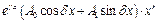
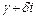
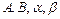 – заданы,
– заданы, 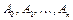 –неизвестные, подлежащие вычислению,
–неизвестные, подлежащие вычислению, 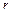 – кратность корня
– кратность корня