
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчеты оптимального использования ресурсов
|
|
Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. И от того, как будут распределяться эти, как правило ограниченные, ресурсы, зависит конечный результат деятельности, бизнеса.
Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя. При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации.
В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое.
Линейное программирование (планирование) – математический метод отыскивания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изображаются в виде прямых линий, обозначающих 1-е степени соответствующих величин.)
Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Она носит название целевой функции.
Ограничения характеризуют имеющиеся возможности решения задачи.
Существо решения задач линейного программирования заключается в нахождении условий, обращающих целевую функцию в минимум или максимум.
Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальным планом.
Линейное программирование (планирование) служит для выбора наилучшего плана распределения ограниченных однородных ресурсов в целях решения поставленной задачи.
В общем виде постановка задачи линейного программирования заключается в следующем.
Условия задачи представляются с помощью системы линейных уравнений или неравенств, выражающих ограничения, налагаемые на использование имеющихся ресурсов:
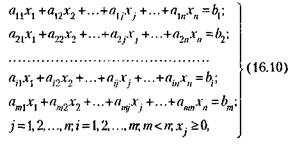
где Xj – искомые величины, содержащие решение поставленной задачи;
aij и bi – известные постоянные величины, характеризующие условия задачи.
Целевая функция (линейная форма) задается в виде
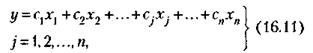
где сj – постоянные коэффициенты (коэффициенты стоимости).
Условия задачи (ограничения) могут быть заданы также в виде неравенств. В этих случаях можно привести систему линейных ограничений к виду (16.10), вводя в каждое линейное ограничение дополнительные неотрицательные неизвестные:
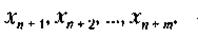
Целевая установка оптимизации заключается в том, чтобы свести ожидаемые при решении данной задачи издержки предприятий к минимуму.
Общая математическая формулировка задачи соответствует условиям (16.10) и (16.11).
Первая строка системы уравнений (16.10)
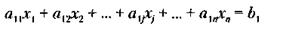
в данном примере означает следующее:
a11 – количество единиц ресурсов вида 1 на первом предприятии;
а12 – количество единиц ресурсов вида 1 на втором предприятии и т. п.;
b1 – общий ресурс ресурсов вида 1 (для всех предприятий);
x1, x2 и.т. д. – искомое количество предприятий типов 1, 2 и т. д.
Вторая строка упомянутой системы уравнений содержит аналогичные величины для ресурсов вида 2 и т. д. Функция цели соответствует формуле (16.11). Требуется обратить в минимум величину
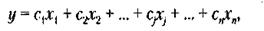
где сj – показатель, характеризующий издержки предприятий.
Пусть т – общее число различных видов ресурсов, которыми располагает собственник, а п – число типов предприятий, между которыми эти ресурсы должны быть распределены. При этом известно, какое количество однородных ресурсов различного вида (i = 1, 2,... т) может быть реализовано на каждом из предприятий данного типа (j = 1, 2,... п), атакже общее количество ресурсов данного вида (bi). Известно также относительное значение издержек на каждом из предприятий (cj).
Задача заключается в том, чтобы наилучшим (оптимальным) образом распределить имеющиеся ресурсы по предприятиям, т. е. найти неизвестные величины xj, требуемые для этого количества предприятий данного типа.
ПРИМЕР
Собственник располагает четырьмя видами ресурсов (m = 4). Это, например, денежные средства, производственные помещения, оборудование, сырье. Ресурсы необходимо распределить между шестью предприятиями (п = 6). Предприятия различаются по экономическим условиям деятельности: месту расположения, системе налогообложения, стоимости энергии, оплате труда и т. д., в связи с чем имеют разные издержки производства. Относительные уровни издержек заданы табл. 16.2.
Таблица 16.2