
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет параметров рыночного равновесия при введении налога на производителей.
|
|
Условие задачи: Предположим, что кривая спроса описывается уравнением Qd=a-b . Р (a=400; b=1), а кривая предложения — уравнением Qs=c+d . Р (c=100; d=2). Правительство ввело налог на производителей в размере m=15 долл. за единицу продукции.
Определите:
1. как изменятся равновесные цена и объем продукции;
2. каков доход государства от введения этого налога;
3. в какой степени пострадают от введения этого налога потребители.
Решение
1. Задача решается аналогично предыдущей (см. Задача 2), с той лишь разницей, что налогом облагаются не потребители, а производители. Определяем параметры рыночного равновесия до введения налога:
400 — Pd = 100 + 2(Pd – 15)
3Pd = 330
Pd = 110 ден. ед.
Ps = 110-15 = 95 ден. ед.
Q1 = 400 – 110 = 290 ед.
Параметры рыночного равновесия после введения налога определяем с помощью уравнений:
Qd = 400 — Р
Qs =100+ 2Р
Qd = Qs
Pd- Ps = 15
Введение налога на производителей приведет к тому, что получаемая ими чистая цена уменьшится. Введение налога на производителей не отразится на цене покупки Pd, а цена продажи будет равна Ps = Pd – 15. Сделав все необходимые подстановки, получаем:
400 — Pd = 100 + 2(Pd – 15)
3 Pd = 330
Pd = 110 долл.
Ps = 110 – 15 = 95 долл.
Q1 = 400 – 110 = 290 ед.
После введения налога на производителей равновесный объем составил 290 ед., а равновесная цена – 110 долл. Таким образом, равновесный объем сократился на 10 ед., а равновесная цена возросла на 10 долл.
2. За каждую единицу проданного товара государство получит 15 долл. Общая сумма налогов, полученных государством, составит:
Дг = Q1 × t = 290 × 15 = 4350 долл.
3. При налоге на производителей каждая единица товара обходится потребителям на 10 долл. дороже (до налога цена покупки составляла 100 долл., при налоге -110 долл.). Часть налоговых поступлений, оплачиваемая потребителями, составит:
Q1 × 10 = 290 × 10 = 2900 долл.
До введения налога цена продажи составляла 100 долл., а после введения налога – 95 долл., т.е. при налоге производители за каждую проданную единицу товара получают на 5 долл. меньше. Часть налоговых поступлений, оплачиваемая производителями, составит:
Q1 × 5 = 290 × 5 = 1450 долл.
Таким образом, при введении налога на производителей покупатели оплачивают в 2 раза большую часть налоговых поступлений, чем производители.
Данные для индивидуального решения:
| № вар | ||||||
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| m |
8.4.. Дана функция издержек монополиста 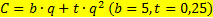 и функция выпуска
и функция выпуска  . Найдите оптимальную цену и объем производства продукции.
. Найдите оптимальную цену и объем производства продукции.
Решение:
Доход монополиста есть  (p - цена продукции), а его прибыль есть
(p - цена продукции), а его прибыль есть  . Из условия задачи
. Из условия задачи  . Подставляя это выражение в формулу прибыли, имеем:
. Подставляя это выражение в формулу прибыли, имеем: 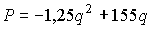 . Максимизируя P по q, получаем:
. Максимизируя P по q, получаем: 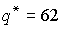 . Следовательно,
. Следовательно, 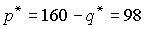 .
.
| № вар. | ||||||

| ||||||

| 0, 25 | 0, 25 | 0, 25 | 0, 25 | 0, 15 | 0, 30 |
| a |
8.5.. Выпуск продукции монополизированной отрасли описывается функцией 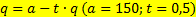 , а средние издержки по производству выражаются функцией
, а средние издержки по производству выражаются функцией  . Найдите оптимальный объем производства и цену.
. Найдите оптимальный объем производства и цену.
Решение:
Заметим, что из условия задачи цену продукции можно выразить через ее выпуск: 
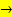
 . Оптимальные значения цены и выпуска максимизируют прибыль монополиста, которая вычисляется как
. Оптимальные значения цены и выпуска максимизируют прибыль монополиста, которая вычисляется как 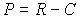 . Доход R найдем по формуле
. Доход R найдем по формуле 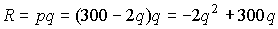 . Издержки C можно определить как произведение средних издержек (т.е. издержек на единицу выпуска) на объем производства:
. Издержки C можно определить как произведение средних издержек (т.е. издержек на единицу выпуска) на объем производства: 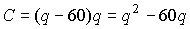 . Тогда имеем
. Тогда имеем 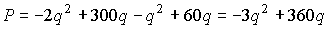 . Найдем максимум этой функции:
. Найдем максимум этой функции:  , значит,
, значит, 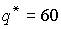 . Тогда оптимальная цена есть
. Тогда оптимальная цена есть  .
.
| № вар. | ||||||

| ||||||

| 0, 5 | 0, 6 | 0, 65 | 0, 5 | 0, 45 | 0, 55 |
| a |
8.6. Известны функции издержек двух фирм, действующих на дуопольном рынке:  . Рыночный спрос
. Рыночный спрос  . Найдите параметры состояния равновесия Курно.
. Найдите параметры состояния равновесия Курно.
Решение:
Рыночный спрос удовлетворяется за счет выпуска обеих фирм, значит,  . В этом случае цена продукции равна
. В этом случае цена продукции равна  . Доход каждой из фирм определим как произведение ее выпуска и цены, тогда их прибыли равны:
. Доход каждой из фирм определим как произведение ее выпуска и цены, тогда их прибыли равны:  ,
,  . Запишем необходимые условия оптимальности:
. Запишем необходимые условия оптимальности:


Используя условия дуополии Курно 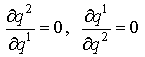 , получаем систему
, получаем систему
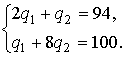
Отсюда  . Равновесная цена есть
. Равновесная цена есть 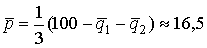 .
.
| № вар. | ||||||

| ||||||
| ||||||
| a |
8.7. Функции общих издержек в условиях дуополии Курно выражаются уравнениями
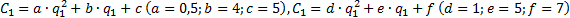 . Рыночный спрос
. Рыночный спрос  . Определите цену равновесия и величину выпусков на данном рынке в условиях равновесия.
. Определите цену равновесия и величину выпусков на данном рынке в условиях равновесия.
Решение:
Из условия равновесия следует  . Значит,
. Значит, 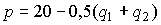 . Доход первой фирмы равен
. Доход первой фирмы равен  , тогда ее прибыль есть
, тогда ее прибыль есть 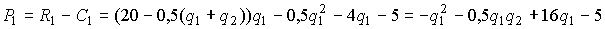 .
.
Аналогично, доход второй фирмы равен 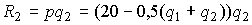 , а прибыль -
, а прибыль - 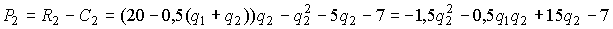 . Отсюда
. Отсюда
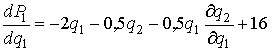 ,
,
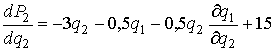 .
.
Учитывая условия 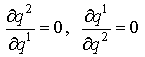 , оптимальные объемы выпусков найдем из системы
, оптимальные объемы выпусков найдем из системы

Значит, 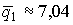 ,
,  . Оптимальная цена есть
. Оптимальная цена есть  .
.
| № вар. | ||||||

| 0, 5 | 0, 5 | 0, 5 | 0, 5 | 0, 6 | 0, 6 |

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||
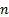
| ||||||
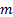
|
8.8. В условиях дуополии Курно рыночный спрос задается соотношением  , а каждая фирма имеет постоянные предельные издержки, равные
, а каждая фирма имеет постоянные предельные издержки, равные  . Найдите объем производства каждой фирмы в состоянии равновесия.
. Найдите объем производства каждой фирмы в состоянии равновесия.
Решение:
Так как спрос удовлетворяется за счет выпуска обеих фирм, то  , отсюда
, отсюда  . Доходы фирм определим как
. Доходы фирм определим как 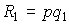 и
и  , а их издержки (используя данные о предельных издержках) - как
, а их издержки (используя данные о предельных издержках) - как  и
и 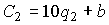 , где a, b - некоторые константы. Прибыли фирм равны разности их доходов и издержек, а, приравнивая к нулю их производные по выпуску и учитывая условия дуополии Курно
, где a, b - некоторые константы. Прибыли фирм равны разности их доходов и издержек, а, приравнивая к нулю их производные по выпуску и учитывая условия дуополии Курно 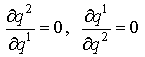 , получаем систему
, получаем систему

Отсюда найдем оптимальные выпуски фирм в состоянии равновесия Курно:  .
.
| № вар. | ||||||
| ||||||
| ||||||
| 1, 5 | 0, 5 | 1, 25 | 0, 75 |
8.9.. Спрос на товар описывается уравнением  . Функция общих издержек фирмы (каждой из фирм) равна
. Функция общих издержек фирмы (каждой из фирм) равна 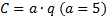 . Найдите равновесную цену и равновесный объем производства
. Найдите равновесную цену и равновесный объем производства
1. в условиях монополии;
2. в условиях дуополии Курно
Решение:
1. В условиях монополии фирма в одиночку удовлетворяет рыночный спрос q, тогда ее прибыль определяется как разность дохода от выпуска и издержек:  .
.
Максимум прибыли соответствует условию  , т.е.
, т.е.  . При этом цена равна
. При этом цена равна 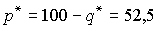 .
.
2. В случае дуополии рыночный спрос удовлетворяется за счет выпуска обеих фирм:  , тогда
, тогда 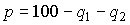 . Прибыль i -ой фирмы определяется по формуле
. Прибыль i -ой фирмы определяется по формуле 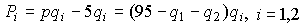 . Необходимые условия оптимальности запишутся в виде
. Необходимые условия оптимальности запишутся в виде 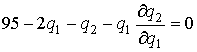 ,
, 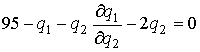 . Так как в дуополии Курно
. Так как в дуополии Курно 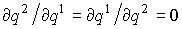 , то получаем систему
, то получаем систему
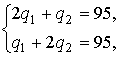
откуда 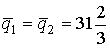 . При этом цена равна
. При этом цена равна 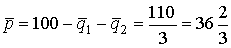 .
.
| № вар. | ||||||

| ||||||
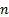
| ||||||
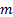
| 1, 25 | 0, 85 | 1, 15 | 0, 95 | 1, 1 | 1, 1 |