Задача 38

Bариант17. Даны координаты вершин пирамиды :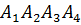

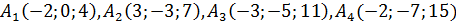
Найти:

1) длину ребра ;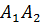

2) угол между ребрам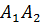и и ;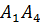

3) угол между ребром 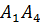и гранью ;

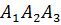4) площадь грани ;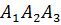

5) объем пирамиды;

6) уравнение прямой ;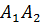

7) уравнение плоскости ;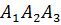

8) уравнение высоты, опущенной из вершины ;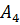

9) сделать чертеж.

Решение.

1) с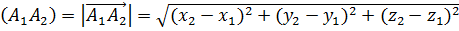

с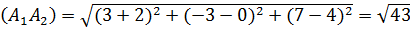

2)

, , ,

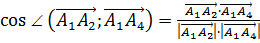
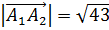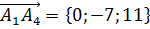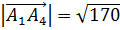
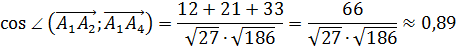
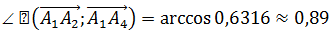или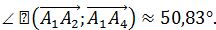

3) Угол φ между прямой и плоскостью вычисляется по формуле

.

Направляющий вектор 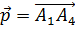прямой 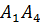имеет координаты 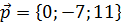,. Плоскость 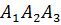задается уравнением

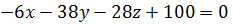(вывод уравнения см. в п.7). Тогда синус угла φ между прямой 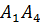и плоскостью 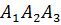вычисляетсятак

sinφ =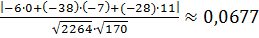

Отсюда φ =arcsin() 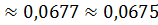или φ = .

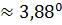4) 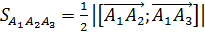или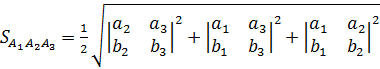

где 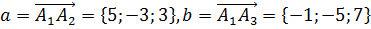.Поэтому

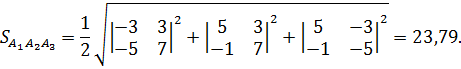
5)

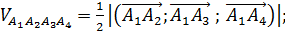
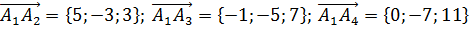
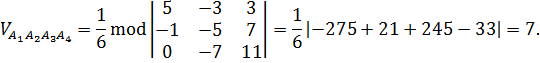
6) Прямая проходит через точки 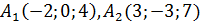поэтому применяя уравнение прямой , получаем:

,

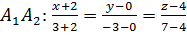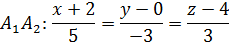
7) Уравнение плоскости имеет вид:

поэтому

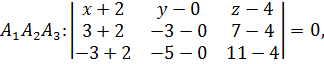
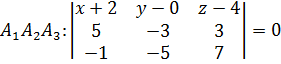
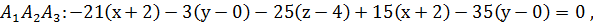
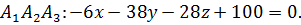
8) Необходимо найти уравнение прямой l, проходящей через точку 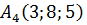и перпендикулярную плоскости 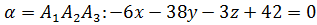. Так как прямая l перпендикулярна плоскости, то она параллельна вектору ее нормали 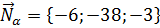. Поэтому направляющим вектором прямой l является вектор нормали заданной плоскости: .

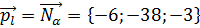Теперь запишем искомое уравнение прямой, проходящей через точку 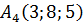в направлении вектора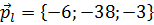

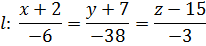
9)
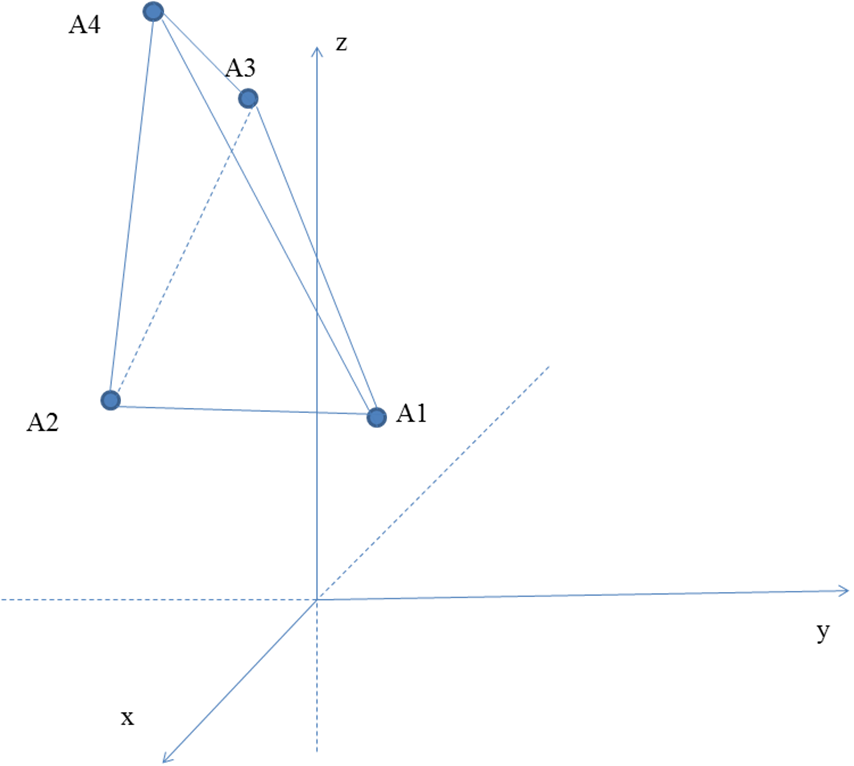