
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
в. Определение усилий по линиям влияния
|
|
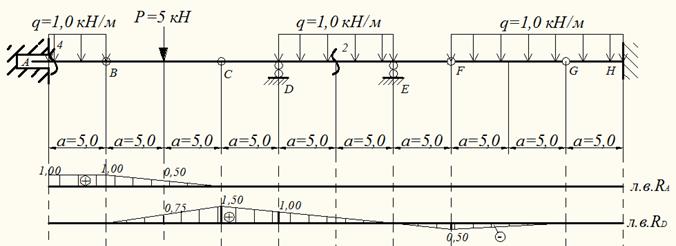
Рис.1. Схема многопролетной балки и нагрузки
А. Построение эпюр Q и M
Для определения внутренних усилий строим «поэтажную» схему взаимодействия отдельных балок. Построение поэтажной схемы начинаем с определения «основной» балки. Для этого необходимо разделить все сооружение на части (убрать шарниры). Та балка, которая при этом останется геометрически неизменяемой и будет основной. В нашем случае это балка GH. Остальные балки являются вспомогательными.
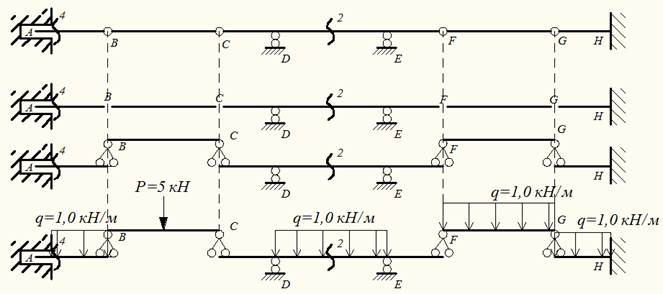
Рис.2 «Поэтажная» схема балки
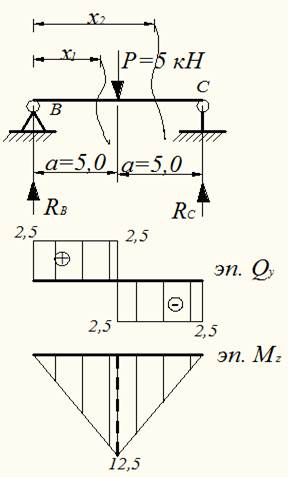 Аналитический расчет начнем с верхней балки ВС:
Аналитический расчет начнем с верхней балки ВС:
Определим опорные реакции:
|
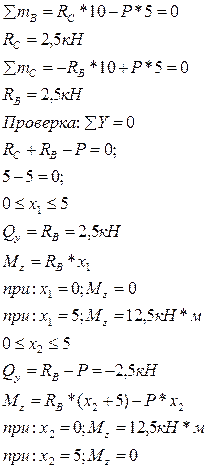
Эпюры Qи Mдля балки ВС построены на рис. 3
Затем рассчитаем балку FG
Определим опорные реакции:
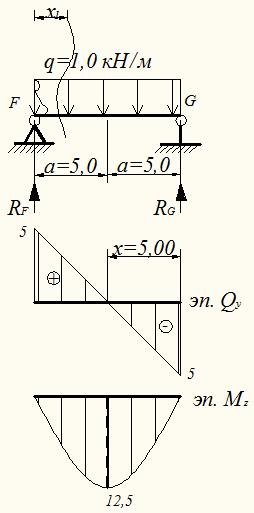
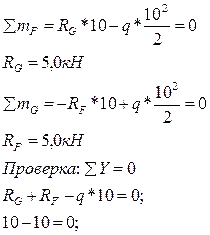
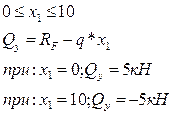
В сечении х1=5/1=5, 0м – вершина параболы на эпюре МZ
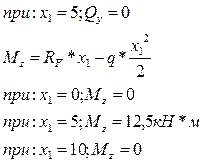
Рис.4
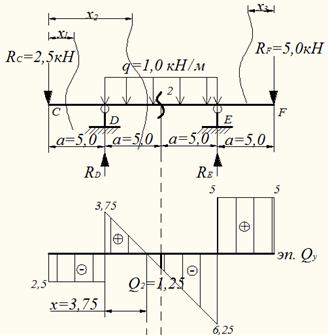
Далее рассчитаем балку CDEF
Из поэтажной схемы видно, что на балку CDEF кроме равномерно распределенной нагрузки q, действует усилия RС и RF от балок ВС и FG.
Определим опорные реакции:
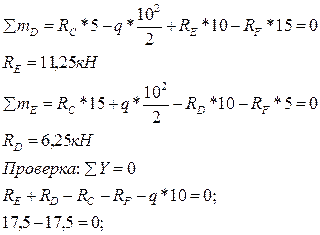
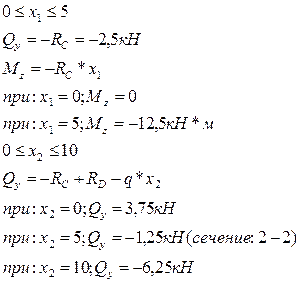
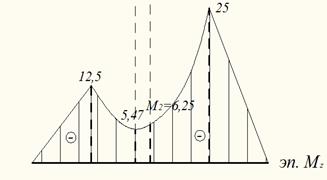 В сечении х2=3, 75/1=3, 75м – вершина параболы на эпюре МZ
В сечении х2=3, 75/1=3, 75м – вершина параболы на эпюре МZ
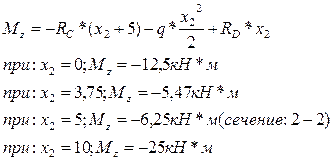
|
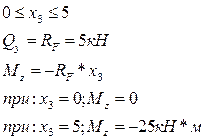
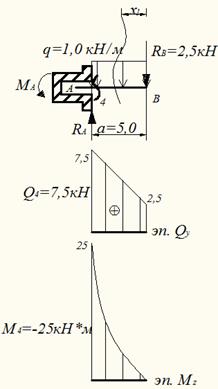
Теперь рассчитаем балку АВ
Из поэтажной схемы видно, что на балку AB кроме равномерно распределенной нагрузки q, действует усилие RВ от балки ВС.
Определим опорную реакцию RA:
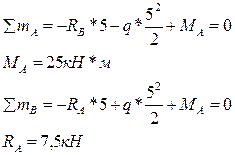
|
|
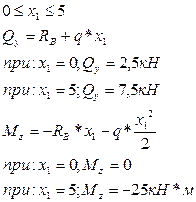
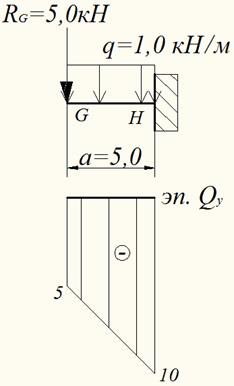 Далее рассчитаем балку GH
Далее рассчитаем балку GH
Из поэтажной схемы видно, что на балку GH кроме силы равномерно распределенной нагрузки q=1кН/м, действует усилие RG от балки FG.
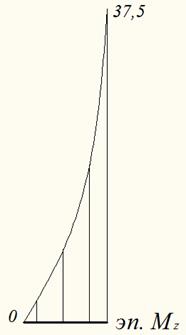
В данном случае опорные реакции, также как и в случае с балкой АВ определять нет необходимости, т.к. двигаясь от сечения G можно определить значения и поперечной силы и изгибающего момента:
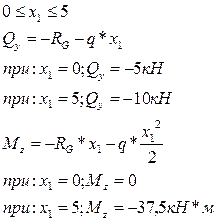
|
Построенные эпюры для отдельных балок покажем на общем чертеже (рис.8)
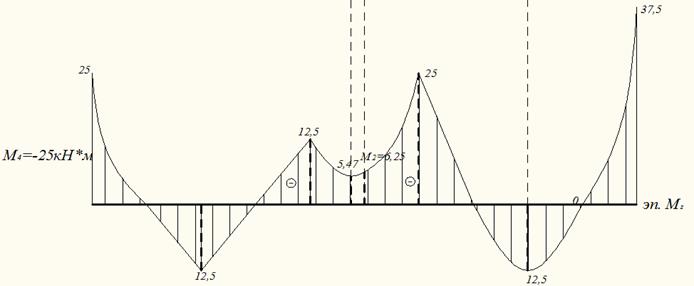
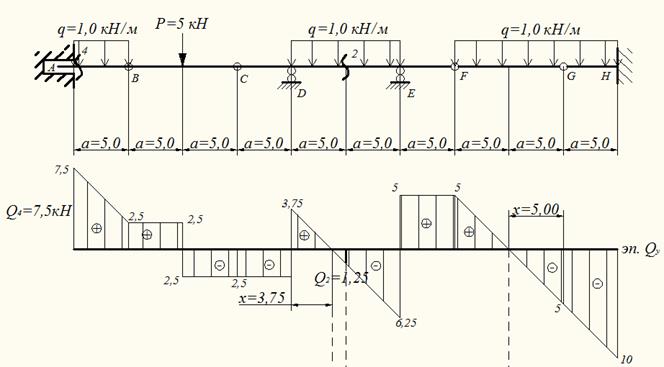
Рис.8
б. Построение линий влияния (расчет на подвижную нагрузку)
Линии влияния необходимы для расчета сооружения на подвижную нагрузку. При построении линии влияния считается, что по сооружению перемещается единичная сосредоточенная сила. График, отображающий изменение усилия в зависимости от положения единичной силы, называется линией влияния.
Линия влияния опорной реакции RА
Рассмотрим балку АВ по которой движется единичная сила F=1. Составим уравнение равновесия:
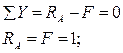
Т.е. в пределах балки АВ линия влияния RA равна 1 и параллельна осевой линии. При движении единичной силы по балке ВС на балку АВ действует усилие RВ, когда сила находится над точкой С усилие RВ =0 балка АВ не загружена и RA=0. Когда сила движется по балке CDEF балка АВ не загружены и RA=0. По указанным ординатам строится линия влияния RА (см. рис. 9).
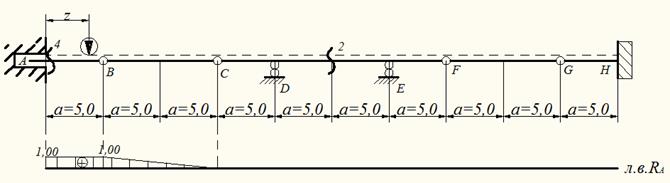
Рис.9
Линия влияния опорной реакции RD
Рассмотрим балку CDEF по которой движется единичная сила F=1. Составим уравнение равновесия:
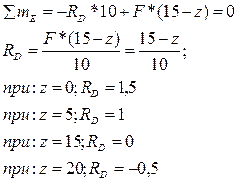
При движении единичной силы по балке BC на балку CDEF действует усилие RC, когда сила находится над точкой B усилие RC =0 балка CDEF не загружена и RD=0. Когда сила движется по балке FG в точке Е на балку CDEF, действует усилие RF, но когда сила находится в точке G усилие RF=0 и балка CDEF не загружены и RD=0. По указанным ординатам строится линия влияния RD (см. рис. 10).
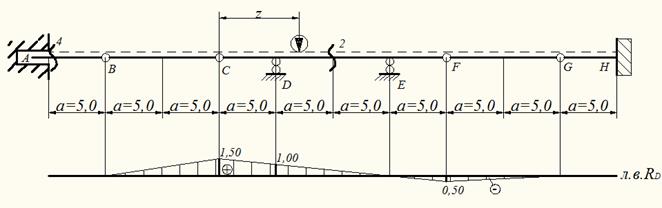
Рис.10
Линия влияния опорной реакции RE
Рассмотрим балку CDEF по которой движется единичная сила F=1. Составим уравнение равновесия:
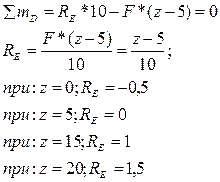
При движении единичной силы по балке BC на балку CDEF действует усилие RC, когда сила находится над точкой B усилие RC =0 балка CDEF не загружена и RE=0. Когда сила движется по балке FG в точке Е на балку CDEF, действует усилие RF, но когда сила находится в точке G усилие RF=0 и балка CDEF не загружены и RE=0. По указанным ординатам строится линия влияния RE (см. рис. 11).
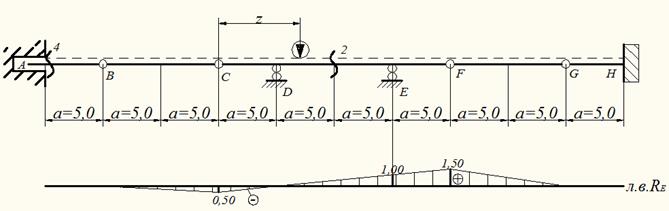
Рис.11
Линия влияния изгибающего момента М2
Рассмотрим балку CDEF с заданным сечением 2-2 (при решении данной задачи используем значения опорных реакций, определенных выше). Рассмотрим случая:
1. Единичная сила движется левее сечения 2-2, тогда из условия равновесия правой отсеченной части:
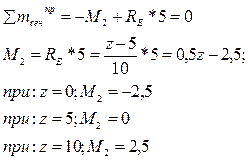
По этим данным строится левая часть линии влияния М2
2. Единичная сила движется правее сечения 2-2, тогда из условия равновесия левой отсеченной части:
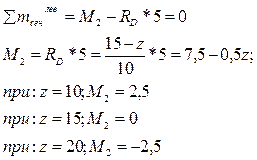
По этим данным строится правая часть линии влияния М2
При движении единичной силы по балке BC на балку CDEF действует усилие RC, когда сила находится над точкой B усилие RC=0 балка CDEF не загружена и M2=0. Когда сила движется по балке FG в точке Е на балку CDEF, действует усилие RF, но когда сила находится в точке G усилие RF=0 и балка CDEF не загружены и M2=0. По указанным ординатам строится линия влияния M2 (см. рис. 12).
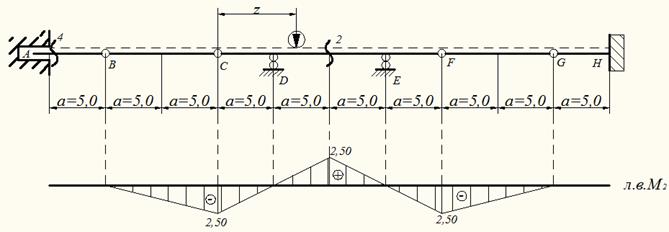
Рис.12
Линия влияния поперечной силы Q2
Чтобы построить линию влияния поперечной силы в заданном сечении 2-2 рассмотрим сначала балку CDEF. Рассмотрим также как и в примере с изгибающим моментом 2 случая:
1. Единичная сила перемещается левее сечения 2-2. Из условия равновесия правой отсеченной части:
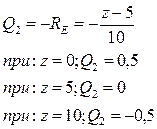
По этим значениям строится левая часть линии влияния Q2
2. Единичная сила перемещается правее сечения 2-2:
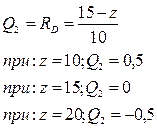
По данным значениям строится правая часть линии влияния
При движении единичной силы по балке BC на балку CDEF действует усилие RC, когда сила находится над точкой B усилие RC=0 балка CDEF не загружена и Q2=0. Когда сила движется по балке FG в точке Е на балку CDEF, действует усилие RF, но когда сила находится в точке G усилие RF=0 и балка CDEF не загружены и Q2=0. По указанным ординатам строится линия влияния Q2 (см. рис. 13).
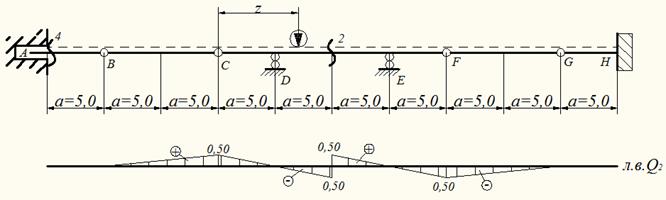
Рис.13
Линия влияния изгибающего момента М4
Рассмотрим балку AB с заданным сечением 4-4.
Определим опорные реакции RA и MA
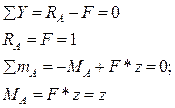
Рассмотрим случая:
1. Единичная сила движется левее сечения 4-4, тогда из условия равновесия правой отсеченной части:
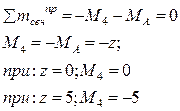
По этим данным строится левая часть линии влияния М4
2. Единичная сила движется правее сечения 4-4, тогда из условия равновесия левой отсеченной части:
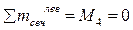
По этим данным строится правая часть линии влияния М4
При движении единичной силы по балке BC в точке B на балку AB действует усилие RB, но когда единичная сила находится над сечением C усилие RB=0, балка AB не загружена и М4=0. По указанным ординатам строится линия влияния М4 (см. рис.14).
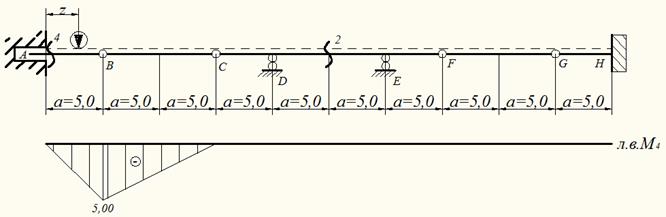
Рис.14
Линия влияния поперечной силы Q4
Чтобы построить линию влияния поперечной силы в заданном сечении 4-4 рассмотрим балку AB. Рассмотрим также как и в примере с изгибающим моментом 2 случая:
1. Единичная сила перемещается левее сечения 4-4. Из условия равновесия правой отсеченной части:
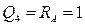
По этим значениям строится левая часть линии влияния Q4
2. Единичная сила перемещается правее сечения 4-4. Из условия равновесия левой отсеченной части::
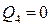
По данным значениям строится правая часть линии влияния
При движении единичной силы по балке BC усилия передаются на балку АВ аналогично примеру с изгибающим моментом. По указанным ординатам строится линия влияния Q4 (см. рис.15).
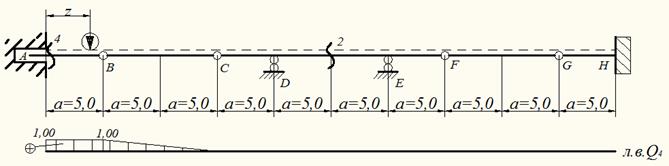
Рис.15
в. Определение усилий по линиям влияния
Усилия RA, RЕ, RD, М2, Q2, М4 и Q4 определяются в соответствии с рис.16 по формуле

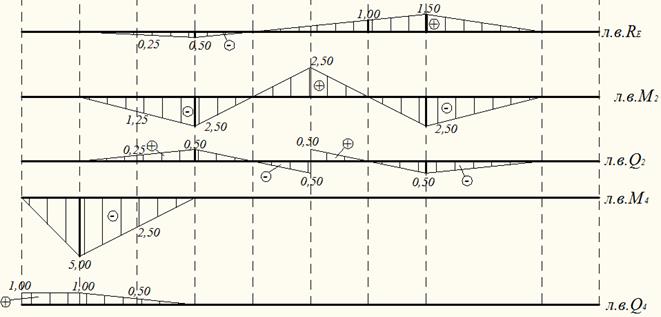 |
Рис.16
1. RA = q*1, 0*5 + P*0, 50 = 7, 5кН (аналитически получилось 7, 5кН)
2. RD = Р*0, 75 + q*1*10 / 2 + q*(-0, 5)*10 / 2 = 6, 25кН (аналитически получилось 6, 25кН)
3. RЕ = Р*(-0, 25) + q*1*10 / 2 +q*1, 5*10 / 2 = 11, 25кН (аналитически получилось 11, 25кН)
4. M2 = Р*(-1, 25) + q*2, 5*10 / 2 + q*(-2, 5)*10 / 2 = -6, 25кН*м (аналитически получилось -6, 25кН*м)
5. Q2 = Р*0, 25 + q*0, 5*5 / 2 + q*(-0, 5)*5 / 2 + q*(-0, 5)*10 / 2 = -1, 25кН (аналитически получилось -1, 25кН)
6. M4 = q*(-5)*5 / 2 +Р*(-2, 5) = -25кН*м (аналитически получилось -25кН*м)
7. Q4 = q*1*5 + Р*0, 5 = 7, 5кН (аналитически получилось 7, 5кН)
Полученные результаты совпадают с результатами аналитического расчета
|