ПРИЛОЖЕНИЕ. треугольник со сторонами, которые могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n › 1 ) является прямоугольным.

Вопрос

Докажите, что:

треугольник со сторонами, которые могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n › 1) является прямоугольным.

Докажите, что обратное утверждение неверно.

Ответ

Сперва мы должны определить, какова самая длинная сторона треугольника со сторонами, которые выражены формулами n2 + 1, n2 – 1 и 2n (где n › 1).

n2+1-2n = (n-1)2.

Если n › 1, то (n – 1)2› 0.

Следовательно, n2+1 – 2n› 0.

Следовательно, n2 + 1› 2n.

Сходным образом (n2 +1) – (n2 – 1) = 2.

Следовательно, n2 + 1› n2 – 1.

Это значит, что n2 + 1 является самой длинной из сторон треугольника со сторонами, которые могут быть выражены формулой n2 + 1, n2 – 1 и 2n (где n › 1).

Для наглядности можно показать это на следующем графике (хотя это ничего не доказывает):

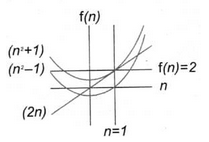
Согласно теореме Пифагора, если сумма квадратов катетов (двух более коротких сторон) равна квадрату гипотенузы (длинной стороны), треугольник является прямоугольным. Следовательно, чтобы доказать, что треугольник прямоугольный, нам нужно показать, что это тот самый случай.

Сумма квадратов двух более коротких сторон равна (n2 -1)2 + (2n)2.

(n2 -1)2 + (2n)2 = n4 – 2n2 + 1 + 4n2 = n4 + 2n2 + 1.

Квадрат гипотенузы равен (n2 +1)2.

(n2 + 1)2 = n4 + 2n2 + 1.

Таким образом, сумма квадратов коротких сторон равна квадрату длинной стороны. Следовательно, треугольник является прямоугольным.

А утверждение, обратное утверждению: «Треугольник со сторонами, которые могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n ›1) прямоугольный», – это: «Прямоугольный треугольник имеет стороны, которые могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n › 1)».

И это значит, что нужно найти треугольник, который будет прямоугольным, но стороны которого не могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n › 1).

Итак, пусть гипотенуза прямоугольного треугольника АВС будет АВ.

Пусть АВ = 65.

Пусть ВС = 60.

Тогда СА = (АВ2 – ВС2)=

= (652 – 602) = (4225 – 3600) = (625) = 25.

Пусть АВ = n2 +1 = 65.

Тогда n = (65 – 1) = V64 – 1 = 8.

Следовательно, (n2 – 1) = 64 – 1 = 6ЗВССА = 25.

И 2n = 16ВС = 60СА = 25.

Следовательно, треугольник АВС является прямоугольным, но его стороны не могут быть выражены формулами n2 + 1, n2 – 1 и 2n (где n ›1). Что и требовалось доказать.

[2]

[3]

[4]

[5]

[6]

[7]

[10]

[11]