
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дополнительные задачи. 1.Найдите двузначное число, если количество единиц в нем на 4 больше количества десятков, а произведение искомого числа на сумму его цифр равно 90.
|
|
1. Найдите двузначное число, если количество единиц в нем на 4 больше количества десятков, а произведение искомого числа на сумму его цифр равно 90.
2. Если от двузначного числа отнять произведение его цифр, то получится 25. Найдите это двузначное число, если известно, что оно в 5 раз больше суммы своих цифр.
3. Двузначное число в три раза больше произведения своих цифр. Если к этому двузначному числу прибавить 18, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите это число.
4. Сумма квадратов цифр двузначного числа равна 13. Если цифры поменять местами, то получится число, которое меньше данного на 9. Найдите это число.
5. Сумма цифр трехзначного числа равна 11, а сумма квадратов цифр этого числа равна 45. Если от искомого числа отнять 198, то получится число, записанное теми же цифрами в обратном порядке. Найдите число.
6. Среднее пропорциональное двух чисел на 12 больше меньшего из этих чисел, а среднее арифметическое тех же чисел на 24 меньше большего из них. Найдите эти числа.
7. При делении некоторого двузначного числа на сумму его цифр в частном получается 3, а в остатке 4. Если же это число разделить на произведение его цифр, то в частном получится 2, а в остатке 5. Найдите это число.
8. При перемножении двух положительных чисел, из которых одно на 10 больше другого, ученик допустил ошибку, уменьшив цифру десятков в произведении на 4. Для проверки ответа при делении полученного произведения на меньшее число он получил в частном 39,
а в остатке 22. Найдите искомые множители.
9. Велосипедист доехал от озера до деревни и вернулся обратно, затратив на весь путь 1 ч. От озера до деревни он ехал со скоростью 15 км/ч, а обратно со скоростью 10 км/ч. Чему равно расстояние от озера до деревни?
10. Турист, находящийся в спортивном лагере, должен успеть к поезду на железнодорожную станцию. Если он поедет на велосипеде со скоростью 15 км/ч, то он опоздает на 30 мин. Если же он поедет на автобусе, скорость которого 40 км/ч, то приедет за 2 ч до отхода поезда. Чему равно расстояние от лагеря до станции?
11. От города до поселка автомобиль доехал за 3 ч. Если бы он увеличил скорость на 25 км/ч, то проехал бы это расстояние за 2 ч. С какой скоростью ехал автомобиль и чему равно расстояние от поселка до города?
12. Два велосипедиста отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.
13. Из пункта А в пункт В, расстояние между которыми 18 км, одновременно выезжают два велосипедиста. Скорость одного из них на 5 км/ч меньше скорости другого. Велосипедист, который первым прибыл в В, сразу же повернул обратно и встретил другого велосипедиста через 1ч 20 мин после выезда из А. На каком расстоянии от пункта В произошла встреча?
14. Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 30 км. Если первый выйдет на 2 ч раньше второго, то он встретит второго пешехода через 4, 5 ч после своего выхода. Если второй выйдет на 2 ч раньше первого, то он встретит первого пешехода через 5 ч после своего выхода. С какой скоростью идет каждый пешеход?
15. Расстояние от А до В по железной дороге равно 88 км, а по реке оно составляет 108 км. Поезд из А выходит на 1 ч позже теплохода и прибывает в В на 15 мин. раньше. Найти скорость поезда, если известно, что она на 40 км/ч больше скорости теплохода.
16. Расстояние между двумя пунктами автомобиль должен был проехать за 6 ч. Первые 4 ч он ехал с намеченной скоростью, а затем увеличил ее на 10 км/ч, поэтому в конечный пункт приехал на 20 мин. раньше, чем предполагал. Найти первоначальную скорость автомобиля.
17. (ЕГЭ 2006) За 200 км до станции назначения поезд был задержан у семафора на час. Затем машинист увеличил на 10 км/ч скорость, с которой поезд ехал до остановки, и поэтому поезд прибыл в пункт назначения по расписанию. С какой скоростью ехал поезд после остановки?
18. (ЕГЭ 2003) Экскурсионный автобус выехал из города А в город В, расстояние между которыми равно 250 км. Автобус ехал 2 часа с постоянной скоростью, потом сделал остановку на полчаса. После остановки он ехал со скоростью на 10 км/ч больше первоначальной и приехал в город В в назначенное время. Найдите первоначальную скорость автобуса.
19. На 60 км пути велосипедист тратит на 4 ч больше, чем мотоциклист. Если же он увеличит скорость на 3 км/ч, то на тот же путь потратит в 4 раза больше времени, чем мотоциклист. Найдите скорость велосипедиста.
20. Лодка может проплыть расстояние между двумя селениями, стоящими на берегу, за 4 ч по течению реки и за 8 ч против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.
21. (ЕГЭ 2007) Катер прошел 3 км против течения реки, а затем 28 км по течению, затратив на весь путь 1 ч. Найдите собственную скорость катера, если скорость течении реки 4 км/ч.
22. (ЕГЭ 2007) Расстояние между пристанями А и В равно 24 км (по реке). От пристани А в сторону пристани В отправился плот. Спустя 9 ч от пристани В навстречу плоту вышла моторная лодка, собственная скорость которой 10 км/ч. Найдите скорость плота, если к пристаням А и В плот и лодка прибыли одновременно.
23. (ЕГЭ 2001) Теплоход прошел расстояние от А до В по течению реки за 7 ч, а от В до А – за 14 ч. За какое время проплывет от А до В плот?
24. (ЕГЭ 2003) Катер прошел 45 км по течению реки и 35 км против течения реки за то же время, что он проходит 80 км в стоячей воде. Найдите собственную скорость катера, если скорость течения реки равна 3 км/ч.
25. За 3 часа теплоход прошел 48 км по течению реки и 16 км против течения. В другой раз тот же теплоход за 5 часов прошел 72 км по течению реки и 32 км против течения. Определите скорость течения реки и скорость теплохода в стоячей воде.
26. Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжал мотоциклист?
27. Два туриста вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми равно 14 км. После встречи один из них прошел остальную часть пути за 2 ч 40мин, другой за 1 ч 30 мин. С какой скоростью шел каждый турист?
28. Велосипедист, выезжающий из пункта А, должен приехать в пункт В через 3 часа. Одновременно с ним из пункта С выезжает другой велосипедист и, чтобы успеть приехать в пункт В вместе с первым, он должен проезжать каждый километр на одну минуту скорее, чем первый, так как расстояние от С до В на 6 км больше расстояния от А до В. Определите скорость каждого велосипедиста.
29. Два велосипедиста одновременно выезжают из пунктов А и В навстречу друг другу и встречаются через 2 ч 40 мин. Если бы они выехали из А в В, причем второй на 3 ч позже первого, то второй велосипедист догнал бы первого пройдя ¾ пути от А до В. Сколько времени требуется первому на весь путь из А в В?
30. Чтобы выполнить задание в срок, токарь должен был изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6 дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
31. (2004, пробный ЕГЭ) Два маляра, работая вместе, могут за 1 ч. Покрасить стену площадью 40 м2. Первый маляр, работая отдельно, может покрасить 50 м2 стены, на 4 часа быстрее, чем второй покрасит 90 м2 такой же стены. За сколько часов первый маляр сможет покрасить 100 м2 стены?
32. (ЕГЭ 2008) Два мебельных мастера, работая вместе, могут за 1 неделю собрать 50 столов. Работая отдельно, первый мастер собирает 60 столов на одну неделю дольше, чем такое же число столов собирает второй мастер. За сколько недель первый мастер соберет 40 столов?
33. (ЕГЭ 2008) Двое рабочих, работая вместе, могут сделать за 1 ч 12 деталей. Первый рабочий, работая отдельно, сделает 28 деталей на 1 ч быстрее, чем второй сделает 25 таких деталей. За сколько часов второй рабочий может сделать 50 деталей?
34. Две установки по обогащению руды должны были обработать 54 т руды. Первая обработала часть руды за 2 часа, затем ее сменила вторая, которая за 3 часа обработала всю оставшуюся часть. Сколько тонн руды обрабатывает за час первая установка, если 36 тонн обрабатываются ею на 1 час медленнее, чем второй установкой?
35. Один рабочий может изготовить за 3 часа столько деталей, сколько другой рабочий изготовит за 4 часа. За 5 часов совместной работы рабочие могут изготовить 105 деталей. Сколько деталей за 1 час может изготовить каждый рабочий?
36. Бригада рабочих должна была за несколько дней изготовить 216 деталей. Первые три дня бригада выполняла установленную ежедневную норму, а потом стала изготавливать на 8 деталей в день больше. Поэтому уже за 1 день до срока было изготовлено 232 детали. Сколько деталей в день стала изготавливать бригада?
37. С первого поля собрали 1080 ц пшеницы, со второго 750 ц. Площадь первого поля на 10 га больше второго. Если бы урожайность (с 1 га) первого поля была такой же, как урожайность на втором поле, а урожайность на втором поле такой же, как на первом, то с обоих полей собрали бы одинаковое количество зерна. Сколько центнеров с гектара (какова урожайность) собрали с каждого поля?
38. Бригаде грузчиков поручили перевести 120 контейнеров. После перевозки 36 контейнеров автомобиль заменили более мощным, грузоподъемность которого на 10 контейнеров больше. В результате общее число рейсов по сравнению с первоначально планируемым сократилось вдвое. Сколько контейнеров перевозила за один рейс первая машина?
39. Две фабрики мороженого выпустили вместе 172 тонны мороженого. Вторая фабрика работала на 4 дня больше, но в день мороженого выпускала на 2 тонны меньше. Всего первая фабрика выпустила на 28 тонн меньше, чем вторая. Сколько тонн в день выпускала каждая фабрика?
40. Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объема) за 11 часов. Если бы три насоса наполнили первый танкер, а затем один из них наполнил бы четверть второго танкера, то работа заняла бы 18 часов. За сколько часов три насоса могут наполнить второй танкер?
41. (ЕГЭ 2005) Двум сотрудникам издательства поручили отредактировать рукопись объемом 560 страниц. Один сотрудник, отдав второму 480 страниц рукописи, взял остальные страницы себе и выполнил свою часть работ за время, в 8 раз меньше, чем второй – свою. На сколько страниц меньше первый сотрудник должен был отдать второму (добавив их себе), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?
42. За 3, 5 ч работы первый штамповочный пресс может изготовить 42% всего заказа. Второй пресс за 9 ч работы может изготовить 60% заказа, а скорости выполнения работы на третьем и втором прессах относятся как 6: 5. За какое время будет выполнен весь заказ, если одновременно будут работать все три пресса?
43. Две бригады, работая вместе, могут закончить уборку урожая за 8 дней. Если первая бригада будет работать 3 дня, а вторая 12 дней, то они выполнят 75% всей работы. За сколько дней может закончить уборку урожая каждая бригада, работая отдельно?
44. При одновременной работе двое рабочих могут выполнить некоторое задание за 6 часов. Если половину задания выполнит первый рабочий, а затем оставшуюся часть – второй, то на это потребуется 12 часов 30 минут. Какую часть задания выполняет за 6 часов рабочий с меньшей производительностью?
45. (ЕГЭ 2006) Две трубы вместе наполняют бассейн за 3 ч. Одна первая труба может наполнить бассейн на 2, 5 ч быстрее, чем одна вторая труба. За сколько часов может наполнить бассейн одна первая труба?
46. (ЕГЭ 2006) Токарь и его ученик, работая одновременно, обычно выполняют задание за 5 часов. При этом производительность труда токаря в 3 раза выше производительности ученика. Получив такое же задание и работая по очереди, они справились с заданием за 8 часов работы. Какую часть задания выполнил ученик токаря?
47. (ЕГЭ 2006) Два фермера, работая вместе, могут вспахать поле за 25 ч. Производительности труда первого и второго фермеров относятся как 2: 5. Фермеры планируют работать поочередно. Сколько времени должен проработать второй фермер, чтобы это поле было вспахано за 45, 5 ч.?
48. (ЕГЭ 2006) Отец с сыном должны вскопать огород. Производительность труда у отца в два раза больше, чем у сына. Работая вместе, они могут вскопать весь огород за 4 часа. Однако вместе они проработали только один час, потом некоторое время работал один сын, а заканчивал работу уже один отец. Сколько часов в общей сложности проработал на огороде отец, если вся работа на огороде была выполнена за 7 часов?
49. В арифметической прогрессии первый член равен 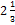 , а разность равна
, а разность равна 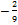 . Является ли число -1 членом этой прогрессии?
. Является ли число -1 членом этой прогрессии?
50. Между числами 6 и -3, 6 вставьте семь чисел так, чтобы получилась арифметическая прогрессия.
51. Сколько нужно сложить последовательных четных натуральных чисел, начиная с 20, чтобы сумма равнялась
120?
52. Найдите сумму всех двузначных чисел.
53. Найдите сумму всех четных трехзначных чисел, делящихся на 3.
54. Найдите сумму всех двузначных чисел, которые при делении на 4 дают в остатке 3.
55. Найдите сумму всех трехзначных натуральных чисел, которые при делении на 11 дают в остатке 5.
56. Найдите сумму членов арифметической прогрессии с тридцатого по сороковой включительно, если 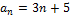 .
.
57. Известно, что при любом n сумма членов некоторой арифметической прогрессии выражается формулой  . Найдите общий член прогрессии.
. Найдите общий член прогрессии.
58. (ЕГЭ 2003) Третий член арифметической прогрессии равен 4, а десятый равен 25. Найдите сумму первых десяти членов данной прогрессии.
59. (ЕГЭ 2003) В арифметической прогрессии сумма первых семи членов равна 21, разность пятого и третьего членов равна -6. На каком месте в этой прогрессии стоит число -21?
60. Третий член арифметической прогрессии равен -6, а сумма второго и пятого членов равна -9. Известно, что один из членов прогрессии равен 15. Найдите его номер.
61. Сумма первого и пятого членов арифметической прогрессии равна 5/3, а произведение третьего и четвертого ее членов равно 65/72. Найдите сумму семнадцати первых членов этой прогрессии.
62. В арифметической прогрессии сумма третьего и пятого членов равна -14, а сумма первых девяти членов равна -45. Сколько отрицательных членов имеет эта прогрессия?
63. В арифметической прогрессии разность тридцать первого и десятого членов составляет 42, а сумма первых пятнадцати членов равна -150. С какого номера начинаются положительные члены этой прогрессии?
64. (ЕГЭ 2003) Десятый член арифметической прогрессии равен 19, а сумма первых пятидесяти членов равна 2500. Найдите сумму третьего, двенадцатого и двадцатого членов этой прогрессии.
65. Планируя выпуск нового электронного прибора, экономисты предприятия определили, что в первый месяц
может быть изготовлено 200 приборов. Далее предполагалось ежемесячно увеличивать выпуск на 20 изделий. За сколько месяцев предприятие сможет выполнить по этому плану поступивший заказ на 11000 приборов?
66. Найдите первый член и разность возрастающей арифметической прогрессии, у которой сумма первых трех членов равна 27, а сумма их квадратов равна 275.
67. Найдите сумму первых двадцати членов арифметической прогрессии, если сумма третьего и восемнадцатого членов равна 8.
68. Сумма первых четырех членов
арифметической прогрессии равна 56, а
сумма последних четырех ее членов рав-на 112. Найдите число членов этой про-
грессии, если первый ее член равен 11.
69. При делении девятого члена ариф-
метической прогрессии на ее второй член
в частном получается 5, а при делении
тринадцатого члена этой прогрессии на
ее шестой член в частном получается 2 и
в остатке 5. Найдите первый член и раз-
ность прогрессии.
70. Сумма шести первых членов
арифметической прогрессии меньше
суммы ее последующих шести членов на
144. На сколько двадцать пятый член
прогрессии больше пятнадцатого члена?
71. Турист, поднимаясь в гору, в пер-
вый час достиг высоты 800 м, а каждый
следующий час поднимался на высоту, на
25 м меньшую, чем в предыдущий. За
сколько часов он достигнет высоты в
5700 м?
72. За установку самого нижнего желе-
зобетонного кольца колодца заплатили
260 рублей, а за каждое следующее коль-
цо платили на 20 рублей меньше, чем за
предыдущее. Кроме того, по окончании
работы было уплачено еще 400 рублей.
Средняя стоимость установки одного
кольца оказалась равной
2020 рублей.
Сколько колец было установлено?
73. Из пунктов А и В навстречу друг
другу выехали одновременно мотоцик-
лист и велосипедист. Мотоциклист про-
ехал в первую минуту 450 м, а в каждую
последующую на 30 м меньше, чем в
предыдущую. Велосипедист же проехал в
первую минуту 60 м, а в каждую следу-
ющую на 10 м больше, чем в предыду-
щую. Какое расстояние проехал велоси-
педист до встречи с мотоциклистом, если
расстояние между А и В 4200 м?
74. (ЕГЭ 2004) В течение календарно-
го года зарплата каждый месяц повыша-
лась на одно и то же число рублей. За
июнь, июль и август зарплата в сумме
составила 9900 р., а за сентябрь, октябрь
и ноябрь – 10350 р. Найдите сумму зар-
плат за весь год.
75. (ЕГЭ 2004) При подготовке к экза-
мену ученик каждый день с 1 по 8 июня
включительно увеличивал количество
решенных задач на одно и то же число. С
1 июня по 4 июня включительно он ре-
шил 24 задачи, а со 2 по 6 июня – 45 за-
дач. Сколько задач ученик решил 8
июня?
76. (ЕГЭ 2004) За 10 дней Карл украл у
Клары 165 кораллов и из них 147 в пер-
вые 7 дней. Каждый день он крал на одно
и то же число кораллов меньше, чем в
предыдущий день. Сколько кораллов
Карл украл в десятый день?
77. Сумма первого и четвертого чле-
нов возрастающей геометрической про-
грессии относится к сумме второго и тре-
тьего членов этой прогрессии как 13: 4.
Найдите первый член прогрессии, если
третий ее член равен 32.
78. Число 180 представить в виде су-
мы четырех слагаемых так, чтобы они
составляли геометрическую прогрессию,
у которой третий член больше первого на
36.
79. Найдите три числа, образующих
геометрическую прогрессию, зная, что
сумма их равна 62, а сумма их квадратов
равна 2604.
80. Геометрическая прогрессия состо-
ит из 6 членов. Найдите ее знаменатель,
зная, что сумма трех первых членов в 8
раз меньше суммы трех последних чле-
нов.
81. Определите сумму бесконечно
убывающей геометрической прогрессии,
если известно, что сумма ее первого и
четвертого членов равна 54, а сумма вто-
рого и третьего 36.
82. Найдите первый член и знамена-
тель бесконечно убывающей геометриче-
ской прогрессии, у которой второй член
равен 6, сумма членов равна
1 суммы
квадратов ее членов.
83. Сумма членов бесконечно убыва-
ющей геометрической прогрессии равна
9, а сумма квадратов членов той же про-
грессии 40, 5. Найдите прогрессию.
84. Сумма трех первых членов геомет-
рической прогрессии равна 42; те же чис-
ла составляют первый, второй и шестой
члены возрастающей арифметической
прогрессии. Найдите эти числа.
85. (2004, пробный ЕГЭ) Если к трем
числам a, b, c, составляющим геометри-ческую прогрессию со знаменателем 4,
прибавить соответственно 49, 45 и 14, то
получатся три числа, составляющие
арифметическую прогрессию. Найдите
сумму чисел a, b, c.
86. Три числа образуют геометриче-
скую прогрессию. Если второе число
увеличить на 2, то прогрессия станет
арифметической, а если после этого уве-
личить последнее число на 9, то прогрес-
сия снова станет геометрической. Найди-
те эти числа.
87. (2004, пробный ЕГЭ) Если к четы-
рем числам a, b, c, d, составляющим
арифметическую прогрессию, прибавить
соответственно 2, 4, 11 и 28, то получатся
четыре числа, составляющие геометриче-
скую прогрессию. Найдите сумму чисел
a, b, c, d.
88. (2009, пробный ЕГЭ) Задана ариф-
метическая прогрессия с первым членом
3 и разностью 4, а также геометрическая
прогрессия с первым членом 1 и знамена-
телем 3. Найдите сумму первых трех сов-
падающих членов этих прогрессий.
89. На счет в банк вносится сумма 1
млн. р., но не сразу, а в течение 20 меся-
цев равными долями в начале каждого
месяца. Какой будет сумма на счете в
конце 10-го месяца, если банк ежемесяч-
но (в последний рабочий день месяца)
начисляет на остаток по счету 4%?
90. Рабочий по норме должен изгото-
вить 500 деталей в месяц. Сдельная рас-
ценка за деталь – 20 р. Перевыполнение
нормы оплачивается по сдельно-
прогрессивной системе: каждые 10 дета-
лей – по удвоенным против предыдущих
расценкам (например, 501-я, 502-я, …,
510-я детали о 40 р.; 511-я, 512-я, …, 520-
я – по 80 р. и т.д.). Какое наименьше чис-
ло деталей должен изготовить рабочий,
чтобы заработать за месяц 30000 р.?
91. (ЕГЭ 2007) Три насоса, работая
вместе, заполняют цистерну нефтью за 5
часов. Производительности насосов отно-
сятся как 4: 3: 1. Сколько процентов объема
цистерны будет заполнено за 8 часов сов-
местной работы второго и третьего насо-
сов?
92. (ЕГЭ 2007) Три насоса, работая
вместе, заполняют бак керосином за 1 час
40 минут. Производительности насосов
относятся как 10: 8: 7. Сколько процентов
объема бака будет заполнено за 2 часа
совместной работы второго и третьего
насосов?
93. Число a составляет от числа b
40%. Найдите, сколько процентов состав-
ляет число b от числа a.
94. Число a составляет 40% от числа
b, число b составляет 50% от числа c.
Сколько процентов составляет число a от
числа c?
95. В магазин для продажи поступили
учебники по физике и математике. Когда
продали 50% учебников по математике и
20% учебников по физике, что составило в
общей сложности 390 книг, то учебников
по математике осталось в 3 раза больше,
чем по физике. Сколько учебников по ма-
тематике и сколько по физике поступило
в продажу?
96. Партия изделий содержит 2% бра-
ка. Среди не бракованных изделий 30% -
первого сорта. Остальные 343 изделия
второго сорта. Сколько всего изделий в
партии?
97. Вклад размером 1500 денежных
единиц разделен на две части. От первой
части, помещенной в банк А, получено за
год процентных денег прибыли 90 д.е., а
от второй части вклада, помещенной в
банк Б – 48 д.е. Какой процент годовых
выплачивает каждый банк, если известно,
что для банка А этот процент на 2 выше,
чем для банка Б?
98. Средняя заработная плата препода-
вателей вузов города за месяц равнялась
765 д.е., а остальных преподавателей –
690 д.е. Средняя заработная плата всех
преподавателей города составляла 714 д.е.
Какой процент от числа преподавателей
города составляют преподаватели вузов?
99. Поле состоит из двух участков. На
первом участке 65% его площади засеяно
пшеницей, на втором – 45%. Известно, что
на всем поле под пшеницей занято 53%
площади поля. Какую часть поля состав-
ляет первый участок?
100. В течение года рабочему была
начислена премия в размере 75% годового
заработка. С 60% общей заработанной
суммы было удержано 12% налога, состальной суммы взят 20%-ный налог.
Общая сумма налога составила 66, 5 ми-
нимальных зарплат. Определить общий
годовой заработок (в количестве мини-
мальных зарплат) до удержания налога.
101. Для изготовления пшеничного
хлеба взято столько килограммов муки,
сколько процентов составляет припек на
эту муку. Для изготовления ржаного хлеба
взято на 10 кг муки больше, т.е. столько
килограммов, сколько процентов состав-
ляет припек на ржаную муку. Сколько ки-
лограммов взято той и другой муки, если
всего выпечено 112, 5 кг хлеба?
102. Фермер купил лошадь и спустя не-
которое время продал ее за 24 д.е. При
этой продаже он теряет столько процен-
тов, сколько стоила ему лошадь. За какую
сумму он ее купил?
103. Продают три куска ткани. Из пер-
вого продали половину, из второго две
трети, а третий кусок, в котором одна
треть всей материи, продали весь. Сколь-
ко процентов ткани продано, если всего ее
осталось вдвое меньше, чем было во вто-
ром куске?
104. Периметр прямоугольника равен
18 см. Если его длину уменьшить на 20%,
а ширину увеличить на 25%, то периметр
не изменится. Найдите площадь прямо-
угольника.
105. За 2 кг огурцов и 3 кг томатов за-
платили 210 д.е. Если огурцы подорожа-
ют на 30%, а помидоры подешевеют на
10%, то за такое же количество продук-
тов будет уплачено 213 д.е. Сколько сто-
ит один килограмм каждого продукта?
106. Одна пара ботинок и куртка об-
щей стоимостью 1200 д.е. были проданы
с прибылью 11, 5%. Определите первона-
чальную стоимость ботинок и куртки,
если от ботинок было получено 25% при-
были, а от куртки 10%.
107. (ЕГЭ 2005) При покупке ребенку
новых лыж с ботинками родителям при-
шлось заплатить на 35% больше, чем два
года назад, причем лыжи подорожали с
тех пор на 20%, а ботинки – на 70%.
Сколько процентов от стоимости лыж с
ботинками составляла два года назад
стоимость лыж?
108. (ЕГЭ 2005) Ежемесячный доход
семьи складывается из зарплаты отца и
зарплаты матери. Зарплату отца увеличи-
ли на 5%, а зарплату матери – на 75%, в
результате чего семейный доход увели-
чился на 15%. Во сколько раз зарплата
матери до повышения была меньше зар-
платы отца?
109. (ЕГЭ 2005) Зимой огурцы стано-
вятся дороже, чем летом, на 45%, а поми-
доры – на 65%. Поэтому овощи для сала-
та «Овощной» из огурцов и помидоров
зимой обходятся на 60% дороже, чем ле-
том. Сколько процентов от стоимости
овощей для такого салата составляет ле-
том стоимость огурцов?
110. (ЕГЭ 2005) В разгар летнего сезо-
на ягоды дешевеют на 15% по сравнению
с началом сезона, а сахар дорожает на
10%, в результате чего приготовление
варенья из ягод по определенному рецеп-
ту обходится на 10% дешевле. Сколько
процентов от стоимости варенья (приго-
товляемого по тому же рецепту) состав-
ляет стоимость ягод в начале сезона?
111. (ЕГЭ 2005) На рынке костюм, со-
стоящий из пиджака и брюк, стоит на
15% дешевле, чем такой же костюм в ма-
газине, причем брюки стоят на 30%, а
пиджак – на 5% дешевле, чем в магазине.
Во сколько раз в магазине пиджак от это-
го костюма дороже брюк?
112. (ЕГЭ 2005) Агрофирма предпола-
гает продать пшеницы на 4% меньше,
чем в прошлом году. На сколько процен-
тов ей надо повысить цену на свою пше-
ницу, чтобы получить за нее на 0, 8%
больше денег, чем в прошлом году?
113. (ЕГЭ 2005) Свиноферма предпо-
лагает продать свинины на 10% меньше,
чем в прошлом году. На сколько процен-
тов ей надо повысить цену на свою сви-
нину, чтобы получить за нее на 8% боль-
ше денег, чем в прошлом году?
114. (ЕГЭ 2007) Объемы ежегодной
добычи угля первой, второй и третьей
шахтами относятся как 8: 9: 10. Первая
шахта планирует уменьшить годовую до-
бычу угля на 4%, а вторая – на 2%. На
сколько процентов должна увеличить го-
довую добычу угля третья шахта, чтобысуммарный объем добываемого за год
угля не изменился?
115. (ЕГЭ 2007) Объемы ежегодной
добычи нефти первой, второй и третьей
скважинами относятся как 4: 5: 7. Плани-
руется уменьшить годовую добычу нефти
из первой скважины на 7% и из второй –
тоже на 7%. На сколько процентов нужно
увеличить годовую добычу нефти из тре-
тьей скважины, чтобы суммарный объем
добываемой за год нефти не изменился?
116. (ЕГЭ 2007) Магазин выставил на
продажу товар с наценкой 50% от заку-
почной цены. После продажи 0, 75 всего
товара магазин снизил назначенную цену
на 40% и распродал оставшийся товар.
Сколько процентов от закупочной цены
товара составила прибыль магазина?
117. (ЕГЭ 2007) Магазин выставил на
продажу товар с наценкой 50% от заку-
почной цены. После продажи 0, 9 всего
товара магазин снизил назначенную цену
на 40% и распродал оставшийся товар.
Сколько процентов от закупочной цены
товара составила прибыль магазина?
118. (ЕГЭ 2008) Подарочный набор со-
стоит из трех сортов конфет. Массы кон-
фет первого, второго и третьего сортов в
этом наборе относятся как 3: 9: 20. Массу
конфет первого сорта увеличили на 8%, а
второго – на 4%. На сколько процентов
надо уменьшить массу конфет третьего
сорта, чтобы масса всего набора не изме-
нилась?
119. За год фруктовый набор, состоя-
щий из яблок, груш и апельсинов, подо-
рожал на 29% из-за того, что цена яблок
выросла на 20%, цена груш – на 30%, а
апельсины подорожали в полтора раза.
Сколько процентов исходной стоимости
набора составляла стоимость яблок, если
стоимость апельсинов в наборе составля-
ла 20%?
120. Музыкальный театр объявил
конкурс для поступления в оркестр. Пер-
воначально предполагалось, что число
мест для скрипачей, виолончелистов и
трубачей распределится в отношении
1, 6: 1: 0, 4. Однако затем было решено уве-
личить прием, и в результате скрипачей
было принято на 25% больше, а виолон-
челистов на 20% меньше, чем ранее
намечалось. Сколько музыкантов каждо-
го жанра было принято в оркестр, если
всего приняли 32 человека?
121. В первой цистерне на 25% нефти
меньше, чем во второй и третьей вместе,
а во второй на 10 тонн меньше, чем в тре-
тьей, и на 50% меньше, чем в первой.
Сколько тонн нефти в каждой цистерне?
122. (ЕГЭ 2005) Двум операторам по-
ручили набрать на компьютере текст
книги объемом 315 страниц. Один опера-
тор, отдав второму 144 страницы книги,
взял остальные страницы себе. Первый
выполнил свою работу за 19 дней, а вто-
рой свою – за 12 дней. На сколько про-
центов нужно было увеличить часть ра-
боты второго оператора (уменьшив часть
работы первого), чтобы они, работая с
прежней производительностью, выпол-
нили свою работу за одинаковое число
дней?
123. При продаже товара по цене 220
рублей за 1 кг магазин получает 10%
прибыли. Если продать этот товар по
цене 180 рублей за 1 кг, то магазин поне-
сет убыток в сумме 4300 рублей. Сколько
килограммов этого товара имеется в ма-
газине?
124. Однозначное число увеличили на
10 единиц. Если полученное число уве-
личит на столько же процентов, как в
первый раз, то получится 72. Найдите
первоначальное число.
125. Букинистический магазин продал
книгу со скидкой в 10% от первоначаль-
ной стоимости и получил при этом 8%
прибыли. Какую прибыль в процентах
предполагал получить магазин до скид-
ки?
126. Две противоположные стороны
прямоугольника удлинили на 10%, а дру-
гие две укоротили на 10%. На сколько
процентов изменится площадь прямо-
угольника?
127. На сколько процентов увеличится
объем прямоугольного параллелепипеда,
если длину и ширину его увеличить на
10%, а высоту уменьшить на 10%?
128. За первый квартал автозавод вы-
полнил 25% годового плана выпуска ав-
томашин. Число машин, выпущенных за
второй, третий и четвертый кварталы, оказалось пропорционально числам
11, 25; 12 и 13, 5. Определите перевыпол-
нение годового плана в процентах, если
во втором квартале автозавод дал про-
дукции в 1, 08 раза больше, чем в первом.
129. За некоторый период времени ко-
личество акций у господина Иванова
увеличилось на 15%. На сколько процен-
тов увеличилась общая стоимость акций
господина Иванова, если цена каждой
акции увеличилась на 20%?
130. Цена товара была снижена на
10%, но за счет повышения спроса за
день было продано больше товара, в ре-
зультате чего дневная выручка от прода-
жи увеличилась на 17%. На сколько про-
центов увеличилось количество продан-
ного за день товара?
131. В январе завод выполнил 105%
плана, а в феврале дал продукции на 4%
больше, чем в январе. На сколько про-
центов завод перевыполнил двухмесяч-
ный план?
132. Цветной телевизор два месяца
назад стоил на 20% дешевле, чем месяц
назад, когда он стоил на 10% дешевле,
чем сейчас. На сколько процентов де-
шевле стоил телевизор два месяца назад,
чем сейчас?
133. Скорость автомобиля на шоссе на
12, 5% больше скорости по грунтовой до-
роге, а время, за которое он проехал рас-
стояние по грунтовой дороге, на 10%
меньше, чем на шоссе. На сколько про-
центов расстояние по шоссе больше рас-
стояния по грунтовой дороге?
134. Объем строительных работ уве-
личился на 80%. На сколько процентов
нужно увеличить число рабочих, если
производительность труда повысится на
20%?
135. Радиус окружности увеличен на
25%. На сколько процентов увеличится
площадь круга?
136. На сколько процентов уменьшит-
ся радиус круга, если его площадь
уменьшится на 36%?
137. Скорость поезда увеличилась с 70
км/ч до 80 км/ч. На сколько процентов
уменьшилось время, затрачиваемое поез-
дом на один и тот же путь?
138. В связи с финансовыми пробле-
мами дирекция предприятия уменьшила
продолжительность рабочего дня с 8 до 7
часов. На сколько процентов предстоит
рабочим повысить производительность
труда, чтобы при тех же расценках
сдельной оплаты труда их заработная
плата выросла на 5%?
139. В январе численность сотрудни-
ков НИИ ОХ составляла 25% от числен-
ности сотрудников НИИ АХ. К декабрю
того же года число сотрудников НИИ АХ
уменьшилось на 16%, а суммарное число
сотрудников двух институтов уменьши-
лось на 18%. На сколько процентов
уменьшилось за год число сотрудников
НИИ ОХ?
140. Осенью виноград стоил в 10 раз
дороже картофеля, зимой овощи и фрук-
ты подорожали. На сколько процентов
подорожал картофель, если известно, что
виноград, подорожавший на 100%, стал
стоить в 16 раз дороже картофеля?
141. Товарооборот магазина А в 2007
году составлял 60% от товарооборота ма-
газина В. В 2008 году товарооборот ма-
газина А вырос на 16%, а суммарный
товарооборот двух магазинов уменьшил-
ся на 9%. На сколько процентов умень-
шился товарооборот магазина В в 2008
году по отношению к 2007 году?
142. Производительность цеха после
реконструкции увеличилась на 40%. За-
каз до реконструкции был на 5% больше,
чем после нее. На сколько процентов
время, затрачиваемое на старый заказ до
реконструкции больше времени, затрачи-
ваемого на новый заказ после рекон-
струкции?
143. После реконструкции поточной
линии ее производительность за смену
возросла на 20%, расход электроэнергии
за смену сократился на 10%, а цена одно-
го киловаттчаса электроэнергии за время
реконструкции выросла на 40%. На
сколько процентов увеличились затраты
на электроэнергию в расчете на единицу
продукции?
144. В последнюю декаду месяца по
сравнению с предыдущей число рабочих
в бригаде уменьшилось на 15%, но за
счет повышения производительноститруда оставшихся рабочих выпуск про-
дукции в последней декаде оказался на
10, 5% больше, чем в предыдущей. На
сколько процентов увеличилась произво-
дительность труда?
145. На заводе 20% всех станков были
переведены на повышенную скорость,
благодаря чему производительность
станка повысилась на 80%. На сколько
процентов повысился выпуск продукции?
146. Цех в целом увеличил за год вы-
пуск продукции на 34%, причем 20% ра-
бочих цеха увеличили выпуск продукции
на 50%. На сколько процентов увеличили
выпуск продукции остальные рабочие
цеха?
147. Банк запланировал провести тор-
ги в августе и сентябре. Если объем тор-
гов в августе увеличить в 5 раз, а сентяб-
ре оставить на запланированном уровне,
то суммарный объем торгов возрастет на
300%. Во сколько раз нужно увеличить
план торгов на сентябрь, оставив неиз-
менным план на август, чтобы суммар-
ный объем торгов за два месяца вырос на
400%?
148. По пенсионному вкладу банк вы-
плачивает 12% годовых. По истечении
каждого года эти проценты капитализи-
руются, т.е. начисленная сумма присо-
единяется к вкладу. На данный вид вкла-
да был открыт счет в 80000 рублей, кото-
рый не пополнялся и с которого не сни-
мали деньги в течение 2 лет. Какой доход
был получен по истечению этого срока?
149. Магазин выставил на продажу
шубу, назначив цену на 150% выше
оптовой. В конце сезона эта цена была
снижена на 20%, а на распродаже весной
новая цена была снижена еще на 40% и
шуба была продана за 36000 рублей. Ка-
кую прибыль получил магазин?
150. Цена товара сначала увеличилась
на 10%, а затем уменьшилась на 25% по
сравнению с увеличенной ценой. В ре-
зультате товар подешевел на 7 рублей по
сравнению с его первоначальной ценой.
Сколько стоил товар первоначально?
151. Торговая база закупила у изгото-
вителя партию альбомов и поставила ее
магазину по оптовой цене, которая на
30% больше цены изготовителя. Магазин
установил розничную цену на альбом на
20% выше оптовой. При распродаже в
конце сезона магазин снизил розничную
цену на альбом на 10%. На сколько руб-
лей больше заплатил покупатель по срав-
нению с ценой изготовителя, если на рас-
продаже он приобрел альбом за 70, 2 руб.?
152. На один продукт два раза была
снижена цена, каждый раз на 15%. На
другой продукт, имевший первоначально
ту же цену, что и первый, снизили цену
один раз на х %. Каким должно быть чис-
ло х, чтобы после всех указанных сни-
жений оба продукта снова имели одну и
ту же цену?
153. Для определения оптимального
режима повышения цен социологи пред-
ложили фирме с 1 января повышать цену
на один и тот же товар в двух магазинах
двумя способами. В одном магазине – в
начале каждого месяца (начиная с февра-
ля) на 2 %, в другом – через каждые два
месяца, в начале третьего (начиная с мар-
та) на одно и то же число процентов,
причем такое, чтобы через полгода (1
июля) цены снова стали одинаковыми. На
сколько процентов надо повышать цену
товара через каждые два месяца во вто-
ром магазине?
154. (ЕГЭ 2003) Предприятие умень-
шило выпуск продукции на 20%. На
сколько процентов необходимо теперь
увеличить выпуск продукции, чтобы до-
стигнуть его первоначального уровня?
155. Владелец кинотеатра имел ста-
бильный доход. В целях увеличения при-
были он повысил цену билетов на 80%.
Количество посетителей резко уменьши-
лось. Тогда он снизил новую цену биле-
тов, приведя ее к 90 процентам от перво-
начальной. На сколько процентов владе-
лец кинотеатра снизил новую цену биле-
тов?
156. За первый год предприятие уве-
личило выпуск продукции на 8%. В сле-
дующем году выпуск увеличился на 25%.
На сколько процентов вырос выпуск про-
дукции по сравнению с первоначальным?
157. Цену товара сначала повысили на
20%, затем новую цену товара повысили
на 15%, и наконец, еще повысили на 10%.На сколько процентов всего повысили
первоначальную цену товара?
158. В первый день производитель-
ность труда в цехе выросла на 80%, во
второй выросла на 60%, в третий день
упала 40%. Как изменялась в среднем за
эти три дня производительность труда?
159. Количество студентов в институ-
те, увеличиваясь на одно и то же число
процентов ежегодно, возросло за три года
с 5000 до 6655 человек. На сколько про-
центов увеличивалось число студентов
ежегодно?
160. Себестоимость единицы продук-
ции, которая сначала равнялась 2500 руб.,
после двух последовательных снижений
на одно и то же число процентов снизи-
лась до 2025 рублей. На сколько процен-
тов снижалась себестоимость каждый
раз?
161. Первоначальная себестоимость
единицы продукции была равна 500 руб.
В течение первого года производства она
повысилась на некоторое число процен-
тов, а в течение второго года снизилась
на такое же число процентов, в результа-
те чего она стала равной 480 рублей.
Определите проценты повышения и сни-
жения себестоимости единицы продук-
ции.
162. Кооператив на изготовляемые им
изделия первоначально назначил цену
выше государственной на определенное
число процентов. Через некоторое время
кооператив уценил изделия на то же чис-
ло процентов, в результате цена изделий
стала на 1% меньше государственной. На
какое число процентов кооперативная
цена первоначально превышала государ-
ственную?
163. Зарплату повысили на p %. Затем
новую зарплату повысили на 2 p %. В ре-
зультате двух повышений зарплата уве-
личилась в 1, 32 раза. На сколько процен-
тов зарплата была повышена во второй
раз?
164. После двух повышений зарплата
увеличилась в 1, 43 раза. При этом число
процентов, на которое повысилась зар-
плата во второй раз, было в 3 раза боль-
ше, чем в первый раз. На сколько про-
центов повысилась зарплата во второй
раз?
165. В начале года на сберкнижку бы-
ло положено 1640 тыс. руб., а в конце го-
да после начисления процентов, взято
обратно 882 тыс. руб. Еще через год на
сберкнижке снова оказалось 882 тыс. руб.
Сколько процентов начисляет сбербанк в
год?
166. На оленеводческой ферме стадо
увеличивается в результате естественно-
го прироста и приобретения новых оле-
ней. В начале первого года стадо состав-
ляло 3000 голов, в конце года ферма ку-
пила 700 голов. В конце второго года
стадо составляло 4400 голов. Определите
процент естественного прироста.
167. Цена некоторого товара была сна-
чала повышена на 20%, затем снижена на
400 рублей, и, наконец, снова повышена
еще на 30% по отношению к предыдуще-
му значению. Какова была первоначаль-
ная цена товара, если в результате повы-
шение составило 4%?
168. Некоторая сумма, большая 1000
рублей, была помещена банк, и после
первого периода хранения проценты,
начисленные на вклад, составили 400
рублей. Владелец вклада добавил на счет
еще 600 рублей. После второго периода
хранения и начисления процентов сумма
на счету стала равной 5500 рублям.
Сколько процентов начислялась по вкла-
ду, если процентная ставка банка для
первого и второго периодов хранения
одинакова?
169. В начале года в сбербанк на
книжку было внесено 10000 рублей, по
окончании года было взято обратно 1000
рублей. Сколько процентов должен
начислять сбербанк в год, чтобы по окон-
чании следующего года на книжке оказа-
лось 24000 рублей?
170. (2009, пробный ЕГЭ) Начальный
капитал акционерного общества состав-
ляет 15 миллионов рублей. Ежегодно ка-
питал увеличивался на 25%. Найдите ми-
нимальное количество лет, после кото-
рых капитал акционерного общества пре-
высит 45 миллионов рублей.
171. Смешали 2 литра 15% раствора
кислоты, 4 литра 10% раствора и 5 литров 12% раствора кислоты. Найти кон-
центрацию (в процентах) полученного
раствора.
172. (ЕГЭ 2005) В бидон налили 7 лит-
ров молока однопроцентной жирности и
3 литра молока шестипроцентной жирно-
сти. Какова жирность полученного моло-
ка (в процентах)?
173. (ЕГЭ 2005) В бидон налили 1 литр
молока однопроцентной жирности и 9
литров молока шестипроцентной жирно-
сти. Какова жирность полученного моло-
ка (в процентах)?
174. (ЕГЭ 2005) В трех литрах воды
размешали 5 чайных ложек минерального
удобрения, а в десяти литрах – две. Оба
раствора слили в один бак и получили
раствор удобрения нужной концентра-
ции. Сколько чайных ложек удобрения
нужно размешать в 65 литрах воды для
получения раствора удобрения такой же
концентрации?
175. Слиток сплава серебра с цинком
весом в 3, 5 кг содержал 76% серебра. Его
сплавили с другим слитком и получили
слиток весом в 10, 5 кг, содержание сере-
бра в котором было 84%. Сколько про-
центов серебра содержалось во втором
слитке?
176. (ЕГЭ 2004) Сплав алюминия и
магния отличается большой прочностью
и пластичностью. Первый такой сплав
содержит 5% магния, второй сплав – 3%
магния. Масса второго сплава в 4 раза
больше, чем масса первого сплава. Эти
сплавы сплавили и получили 3 кг нового
сплава. Определите, сколько граммов
магния содержится в новом сплаве.
177. (2004, пробный ЕГЭ) К какому
количеству (в граммах) раствора соли че-
тырехпроцентной концентрации надо до-
бавить 25 граммов раствора соли девяти-
процентной концентрации, чтобы полу-
чить пятипроцентный раствор соли?
178. Масса первого сплава на 3 кг
больше массы второго сплава. Первый
сплав содержит 10% цинка, второй – 40%
цинка. Новый сплав, полученный из двух
первоначальных, содержит 20% цинка.
Определите массу нового сплава.
179. Сосуд содержит 20% раствор кис-
лоты. Из него отлили 5 л, а затем добави-
ли 5 л 10% раствора той же кислоты. В
результате получили 16% раствор.
Сколько кислоты было в сосуде в начале?
180. Имеется сталь двух сортов, один
из которых содержит 5%, а другой – 10%
никеля. Сколько тонн каждого из этих
сортов нужно взять, чтобы получить
сплав, содержащий 8% никеля, если во
втором куске никеля на 4 т больше, чем в
первом?
181. Два раствора, из которых первый
содержал 800 г безводной серной кисло-
ты, а второй – 600 г соединили вместе и
получили 10 кг нового раствора серной
кислоты. Определите вес первого и вто-
рого растворов, вошедших в смесь, если
известно, что процент содержания без-
водной серной кислоты в первом раство-
ре на 10 больше, чем процент содержания
безводной серной кислоты во втором.
182. В 500 кг руды содержится неко-
торое количество железа. После удаления
из руды 200 кг примесей, содержащих в
среднем 12, 5% железа, в оставшейся руде
содержание железа повысилось на 20%.
Какое количество железа осталось еще в
руде?
183. Имеется два раствора поваренной
соли разной концентрации. Если слить
вместе 100 г первого раствора и 200 г
второго, то получится 50%-ный раствор.
Если же слить 300 г первого раствора и
200 г второго, то получится 42%-ный
раствор. Определите процент содержания
поваренной соли в каждом растворе.
184. Имеется два сплава золота и сере-
бра. В одном сплаве количества этих ме-
таллов находятся в отношении 1: 2, в дру-
гом – 2: 3. Сколько граммов нужно взять
от каждого сплава, чтобы получить 19 г
сплава, в котором золото и серебро нахо-
дятся в отношении 7: 12?
185. Один сплав состоит из двух ме-
таллов, входящих в него в отношении 1: 2,
а другой сплав содержит те же металлы в
отношении 2: 3. В каком отношении
необходимо взять эти сплавы, чтобы по-
лучить новый сплав, содержащий те же
металлы в отношении 17: 27?
186. Имеются два сплава меди и цин-
ка. В первом сплаве меди в 2 раза боль-
ше, чем цинка, а во втором меди в 5 раз
меньше, чем цинка. Во сколько раз боль-
ше надо взять второго сплава, чем перво-
го, чтобы получить новый сплав, в кото-
ром цинка было бы в 2 раза больше, чем
меди?
187. В каких пропорциях нужно спла-
вить золото 375-й пробы с золотом 750-й
пробы, чтобы получить золото 500-й
пробы?
188. (ЕГЭ 2004) Первый сплав серебра
и меди содержит 430 г серебра и 70 г ме-
ди, а второй сплав – 210 г серебра и ка-
кое-то количество меди. Сплавили кусок
первого сплава с куском массой 75 г вто-
рого сплава и получили 300 г сплава, ко-
торый содержит 82% серебра. Определи-
те массу (в граммах) второго сплава.
189. (ЕГЭ 2004) Имеются два слитка
сплава серебра и олова. Первый слиток
содержит 360 г серебра и 40 г олова, а
второй слиток – 450 г серебра и 150 г
олова. От каждого слитка взяли по куску,
сплавили их и получили 200 г сплава, в
котором оказался 81% серебра. Опреде-
лите массу (в граммах) куска, взятого от
второго слитка.
190. Смешали 20 л 70%-ного спирта,
30 л 50%-ного спирта и 22, 5 л воды. Ка-
ково процентное содержание спирта в
получившейся меси?
191. Смешали 5 л сливок 35%-ной
жирности с 4 л сливок 20%-ной жирности
и к смеси добавили 1 л чистой воды. Ка-
кова жирность полученной смеси?
192. Кусок сплава меди с оловом мас-
сой 15 кг содержит 20% меди. Сколько
чистой меди необходимо добавить к это-
му сплаву, чтобы новый сплав содержал
40% олова?
193. (ЕГЭ 2003) Влажность сухой це-
ментной смеси на складе составляет 18%.
Во время перевозки из-за дождей влаж-
ность смеси повысилась на 2%. Найдите
массу привезенной смеси, если со склада
было отправлено 400 кг.
194. Свежие грибы содержат по массе
90% воды, а сухие 12%. Сколько полу-
чится сухих грибов из 22 кг свежих?
195. Из 40 т руды выплавляется 20 т
стали, содержащего 6% примесей. Каков
процент примесей в руде?
196. (ЕГЭ 2004) В колбе было 800 г
80%-го спирта. Провизор отлил из колбы
200 г этого спирта и добавил в нее 200 г
воды. Определите концентрацию (в про-
центах) полученного спирта.
197. (ЕГЭ 2004) В колбе было 200 г
80%-го спирта. Провизор отлил из колбы
некоторое количество этого спирта и за-
тем добавил в нее столько же воды, что-
бы получить 60%-ый спирт. Сколько
граммов воды добавил провизор?
198. (ЕГЭ 2004) Латунь – сплав меди и
цинка. Кусок латуни содержит меди на 11
кг больше, чем цинка. Этот кусок латуни
сплавили с 12 кг меди и получили латунь,
в которой 75% меди. Сколько килограм-
мов меди было в куске латуни первона-
чально?
199. (ЕГЭ 2004) Латунь – сплав меди и
цинка. Кусок латуни содержит меди на 60
кг больше, чем цинка. Этот кусок латуни
сплавили со 100 кг меди и получили ла-
тунь, в которой 7% меди. Определите
процент содержания меди в первоначаль-
ном куске латуни.
200. Вычислите массу и пробу сплава
серебра с медью, зная, что сплавив его с 3
кг чистого серебра, получим сплав 900-й
пробы (т.е. в сплаве 90% серебра), а
сплавив с 2 кг сплава 900-й пробы, полу-
чили сплав 840-й пробы.
201. В двух сплавах медь и цинк отно-
сятся как 4: 1 и 1: 3. После совместной пе-
реплавки 10 кг первого сплава, 16 кг вто-
рого сплава и нескольких килограммов
чистой меди получили сплав, в котором
медь и цинк относятся как 3: 2. Определи-
те вес нового сплава.
202. К раствору, содержащему 39 г со-
ли, добавили 1000 г воды, после чего
концентрация соли уменьшилась на 10%.
Найдите первоначальную процентную
концентрацию соли в растворе.
203. Емкость сосуда 8 л. Он наполнен
воздухом, содержащим 16% кислорода.
Из этого сосуда выпускают некоторое
количество воздуха и впускают такое же
количество азота. После чего опять вы-
пускают такое же, как и первый раз ко-
личество смеси, и опять дополняют та-
ким же количеством азота. В новой смеси
оказалось 9% кислорода. Определите, посколько литров смеси выпускали из сосу-
да каждый раз.
204. Из бутыли, наполненной 12%-
ным раствором соли, отлили 1 л раствора
и налили 1 л воды, затем отлили еще 1 л
смеси и опять долили водой. В бутыли
оказался 3%-ный раствор соли. Какова
вместимость бутыли?
205. Из сосуда, емкостью 54 л, напол-
ненного чистой кислотой, вылили не-
сколько литров и долили сосуд водой.
Затем вылили столько же литров смеси,
как в первый раз. Тогда в оставшейся в
сосуде смеси оказалось 24 л кислоты.
Сколько литров кислоты вылили в пер-
вый раз из сосуда?
206. Два человека отправляются из од-
ного и того же места на прогулку до
опушки леса, находящейся в 4, 3 км от
места отправления. Один идет со скоро-
стью 4 км/ч, а другой – со скоростью 4, 6
км/ч. Дойдя до опушки, второй с той же
скоростью возвращается обратно. На ка-
ком расстоянии от точки отправления
произойдет их встреча? Ответ дайте в ки-
лометрах.
207. Численность волков в двух запо-
ведниках в 2009 году составляла 220 осо-
бей. Через год обнаружили, что в первом
заповеднике численность волков возрос-
ла на 10%, а во втором – на 20%. В ре-
зультате общая численность волков в
двух заповедниках составила 250 особей.
Сколько волков было в первом заповед-
нике в 2009 году?
208. Брюки дороже рубашки на 30%, и
дешевле пиджака на 22%. На сколько
процентов рубашка дешевле пиджака?
209. Из пункта А круговой трассы,
длина которой равна 30 км, одновремен-
но в одном направлении стартовали два
автомобилиста. Скорость первого равна
92 км/ч, скорость второго – 77 км/ч. Че-
рез сколько минут первый автомобилист
будет опережать второго ровно на 1 круг?
210. Три килограмма черешни стоят
столько же, сколько пять килограммов
вишни, а три килограмма вишни - столь-
ко же, сколько два килограмма клубники.
На сколько процентов килограмм клуб-
ники дешевле килограмма черешни.
211. Первая труба наполняет бак объ-
емом 600 литров, а вторая труба – бак
объемом 900 литров. Известно, что одна
из труб пропускает в минуту на 3 л воды
больше, чем другая. Сколько литров во-
ды в минуту пропускает вторая труба,
если баки были наполнены за одно и то
же время?