
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ № 2
|
|
|
По дисциплине __________________________________________________________
________________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
|
_____________________________________________________________________________
_____________________________________________________________________________
Автор: студент гр. РТ-08 _____________ /Омадыков К.В./
(подпись) (Ф.И.О.)
Дата: __________________
ПРОВЕРИЛ:
Руководитель проекта: профессор ___________ /Морозов Ю. Т. /
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Задание: Рассчитать параметры двуствольной скважины и построить ее на чертеже.
Исходные данные:
Таблица №1
| Параметр | Значение |
| Угол заложения скважины θ 1, град | |
| Глубина, м: прямолинейного участка скважины h1 от h1 до забоя скважины h2 | |
| Интенсивность искривления, град/м: основного ствола скважины iосн дополнительного ствола скважины iдоп | 0, 04 0, 07 |
| Угол падения рудного тела β, град |
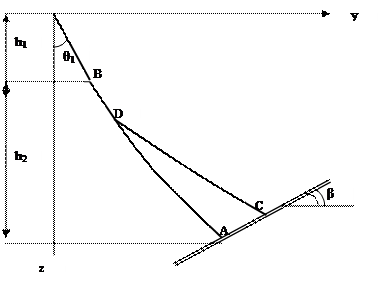 |
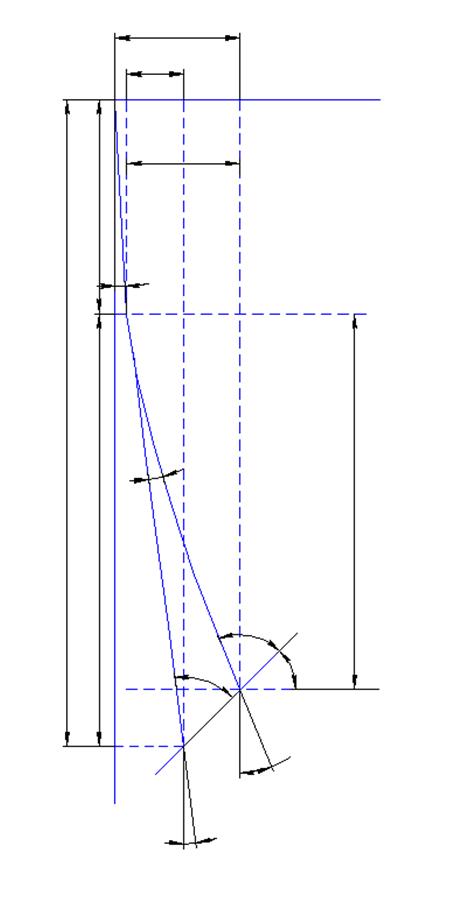
Рис.1. Схема двуствольной скважины.
где ОВ – прямолинейный участок основного ствола; ВА – криволинейный участок основного ствола; DC – дополнительный ствол; АС – рудная зона; точка В – точка начала искривления скважины; точка D – точка забурки дополнительного ствола; Оy и Oz – координатные оси.
Решение:
1. Определим коэффициенты кривизны криволинейной части основного ствола и дополнительного ствола:
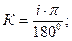

2. Определим радиусы искривления основного и дополнительного стволов:
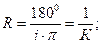
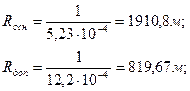
3. Определим параметры прямолинейного участка основного ствола. Зенитный угол в точке В равен зенитному углу на устье скважины, так как скважина на интервале ОВ не меняет своего направления, то есть 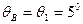 . Уравнение трассы прямолинейного участка запишется в общем виде:
. Уравнение трассы прямолинейного участка запишется в общем виде:
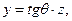 (1)
(1)
где θ – зенитный угол прямолинейной скважины, в нашем случае 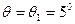 .
.
Таким образом, можем найти координаты точки В, найдя из рис.1, что zB = h1 =125 м:
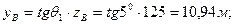
Длина прямолинейного участка из геометрических соображений равна:
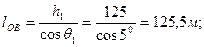
4. Определим параметры участка ВА основного ствола. Уравнение трассы этого участка будет также иметь вид (1), но в качестве углового аргумента под знаком тангенса будет стоять величина: 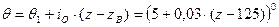 , так как, начиная от точки B, скважина начнет набирать кривизну, меняя свой зенитный угол на величину i O за каждый метр с глубины 125 м.
, так как, начиная от точки B, скважина начнет набирать кривизну, меняя свой зенитный угол на величину i O за каждый метр с глубины 125 м.
В итоге получим уравнение:
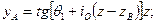 (2)
(2)
Определим координаты точки А, найдя из рис.1, что zА = h1 + h2 =725 м:
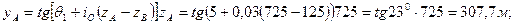
Зенитный угол точки А равен: 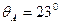 .
.
Длина криволинейного участка скважины равна:
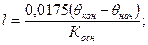
где 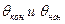 - зенитные углы конечной точки криволинейного участка и начальной точки, соответственно. В нашем случае такими точками являются точки А и В.
- зенитные углы конечной точки криволинейного участка и начальной точки, соответственно. В нашем случае такими точками являются точки А и В.
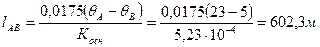
5. Зададимся глубиной забурки дополнительного ствола, то есть зададим координату z точки D, примем zD =300 м, тогда, пользуясь уравнением (2), определим вторую координату и азимут в этой точке:
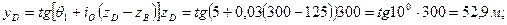
Зенитный угол точки D равен: 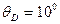 . Длина участка BD равна:
. Длина участка BD равна:
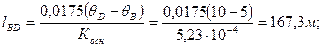
Тогда длина участка ОD равна: 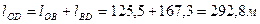
6. Определим параметры дополнительного ствола. Общий вид уравнения трассы дополнительного ствола будет иметь вид (1), но под знаком аргумента тангенса будет стоять выражение: 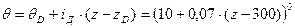 , так как набор кривизны ведется от точки D с θ D=100 и, начиная с 300 м трасса ведет набор кривизны на величину iдоп за каждый метр. Уравнение примет вид:
, так как набор кривизны ведется от точки D с θ D=100 и, начиная с 300 м трасса ведет набор кривизны на величину iдоп за каждый метр. Уравнение примет вид:
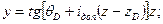
Проблема определения параметров дополнительного ствола состоит в том, что четко не заданы координаты забоя, но воспользуемся тем, что знаем угол наклона рудной зоны и тем, что основной ствол пересекает ее в точке А, координаты которой известны (см. п. 4). Составим уравнение, которое будет описывать геометрию рудной зоны, считая, что уравнение линейное. Пользуясь соображениями аналитической алгебры, получаем уравнение рудной зоны:
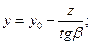 (3)
(3)
где y0 – координата пересечения рудной зоны с дневной поверхностью. Этот параметр найдем, подставив в уравнение (3) координаты точки A:
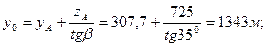
Таким образом, для определения координат точки С получили систему уравнений:
 (4)
(4)
Система (4) сводиться к трансцендентному уравнению, которое можно решить лишь приближенно. Решив данную систему с помощью программы MS Excel, получили координаты точки С: zС =670 м и yC =536, 4 м. Зенитный угол в точке С равен 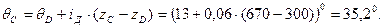
Длина участка DC:
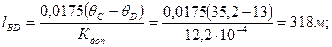
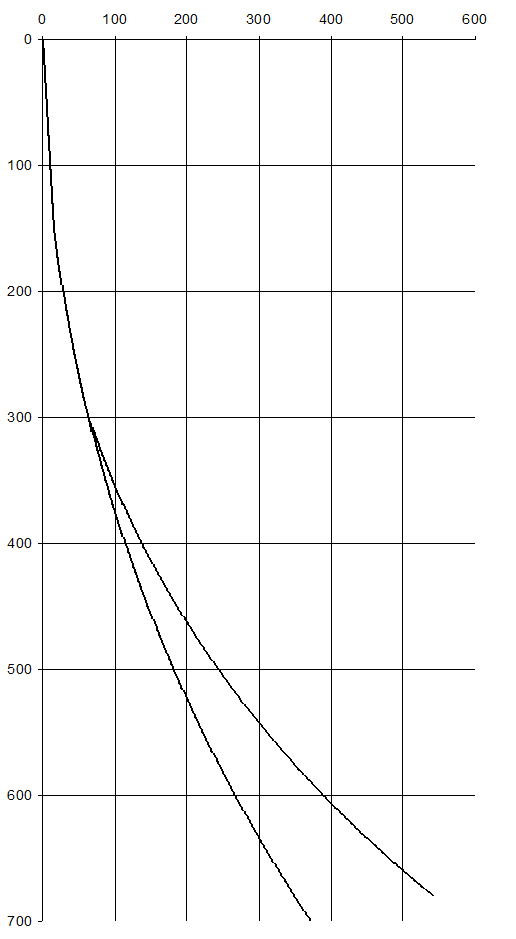
Определили все необходимые параметры двуствольной скважины. По результатам выполняем чертеж.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


|