
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1. Логические выражения
|
|
Логические выражения
Введем в ячейку А1 формулу: =7> 5. Она вернет значение ИСТИНА.
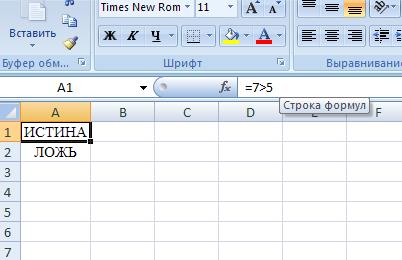
Рисунок 6.2
Скопируем содержимое А1 в А2 и исправим в А2 формулу: = 3> 5.
Эта формула вернет значение ЛОЖЬ.
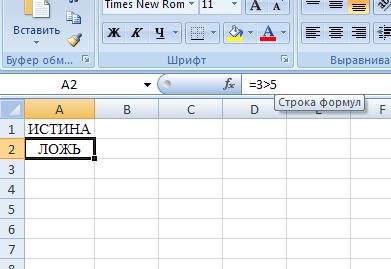
Рисунок 6.3
Правые части обеих формул представляют собой высказывания, т.е. утверждения, относительно которых можно заключить, верны они или нет. Арифметические формулы, которые мы изучали, высказываниями не являются: они предписывают, как по исходным данным вычислить значение, и вопрос об их истинности или ложности не имеет смысла.
Рассмотрим другой пример. Введем в ячейку А4 число 2, а в ячейку В4формулу = A4> 3.Формула возвращает значение ЛОЖЬ.
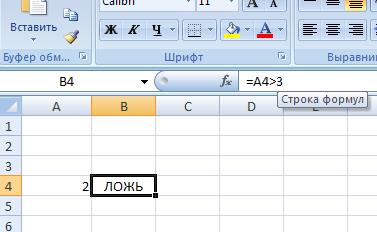
Рисунок 6.4
Введем в А4число 6. Формула возвращает значение ИСТИНА.
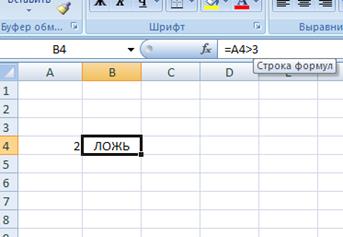
Рисунок 6.5
В В4записан предикат, т.е. высказывание с переменными (в данном случае переменная одна). В зависимости от значенияпеременных предикат может принимать значения ИСТИНА и ЛОЖЬ.В этом примере формула какбы дает ответ на вопрос: " Число (или результат вычислений по формуле), хранящееся в ячейке А4, превышает 3? " В зависимости от значения А4 ответ будет ДА (ИСТИНА) или НЕТ (ЛОЖЬ).
Сравнение двух арифметических выражений, содержащих переменные, дает предикат. В формуле = А4> 3 еесоставные части (А4 и 3) можно считать арифметическими выражениями, только очень простыми. Более сложный пример: = (А4^2-1) > (2*А4+1). Вэтом выражении скобки можно опустить, потому что арифметические операции имеют более высокий приоритет, чем операции сравнения, но скобки придают формуле наглядность.
У логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Поэтому логические функции можно задать таблицей, где перечислены все возможные значения аргументов и соответствующие им значения функций. Такие таблицы называются таблицами истинности.
Ниже представлена таблица для функции НЕ
Таблица 4
| x | НЕ(x) |
| ЛОЖЬ | ИСТИНА |
| ИСТИНА | ЛОЖЬ |
Таблица для функций И и ИЛИ имеет вид
Таблица 5
| x | y | И(x, y) | ИЛИ(x, y) |
| ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
| ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА |
| ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА |
| ИСТИНА | ИСТИНА | ИСТИНА | ИСТИНА |
Функция НЕ может иметь только один аргумент, а функции И и ИЛИ могут иметь два и более аргументов.