Детерминированность

Другие способы описания

1. Диаграмма состояний ( или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой размеченный ориентированный граф, вершины которого — состояния КА, дуги — переходы из одного состояния в другое, а метки дуг — символы, по которым осуществляется переход из одного состояния в другое. Если переход из состояния q₁ в q₂ может быть осуществлен по одному из нескольких символов, то все они должны быть надписаны над дугой диаграммы.
2. Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается состояние, в которое должен перейти автомат, если в данном состоянии он считал данный входной символ.

Детерминированность

Конечные автоматы подразделяются на детерминированные и недетерминированные.

Детерминированный конечный автомат

• Детерминированным конечным автоматом (ДКА) называется такой автомат, в котором нет дуг с меткой ε (предложение, не содержащее ни одного символа), и из любого состояния по любому символу возможен переход в точности в одно состояние.
• Недетерминированный конечный автомат (НКА) является обобщением детерминированного. Недетерминированность автоматов достигается двумя способами:

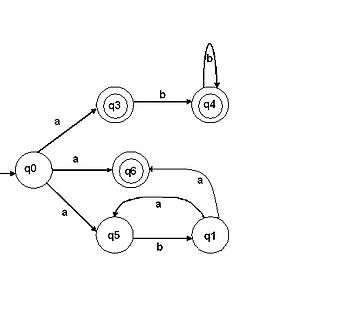
Существуют переходы, помеченные пустой цепочкой ε	Из одного состояния выходит несколько переходов, помеченных одним и тем же символом

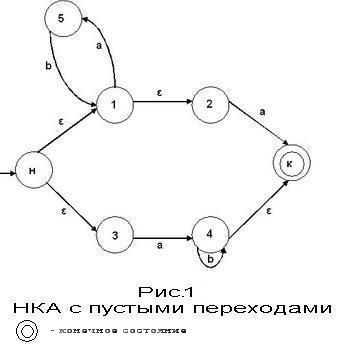
Если рассмотреть случай, когда автомат задан следующим образом: 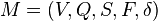, где 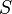— множество начальных состояний автомата, такое, что 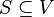, то появляется третий признак недетерминированности — наличие нескольких начальных (стартовых) состояний у автомата .

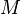Теорема о детерминизации утверждает, что для любого конечного автомата может быть построен эквивалентный ему детерминированный конечный автомат (два конечных автомата называют эквивалентными, если их языки совпадают). Однако поскольку количество состояний в эквивалентном ДКА в худшем случае растёт экспоненциально с ростом количества состояний исходного НКА, на практике подобная детерминизация не всегда возможна. Кроме того, конечные автоматы с выходом в общем случае не поддаются детерминизации.

В силу последних двух замечаний, несмотря на бо́ льшую сложность недетерминированных конечных автоматов, для задач, связанных с обработкой текста, преимущественно применяются именно НКА.