Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кручение
|
|
Кручение – случай простой деформации, при котором в поперечных сечениях возникают только крутящие моменты, а другие внутренние силовые факторы отсутствуют. При этом в поперечных сечениях имеют место только касательные напряжения, а нормальные равны нулю: σ x=σ y=σ z=τ yz=0, τ yx≠ 0.
Крутящий момент (Мt) в произвольном сечении стержня равен алгебраической сумме моментов всех внешних сил, взятых по одну сторону от сечения, относительно продольной оси. Правило знаков для
крутящих моментов принято следующее. При стремлении
вращать отсеченную часть по ходу часовой стрелки «+»,
против хода «-». Смотреть необходимо со стороны сечения.
С целью упрощения расчетов стержней круглого поперечного сечения в сопротивлении материалов приняты следующие гипотезы:
1. Все поперечные сечения круглого стержня при кручении остаются плоскими и только поворачиваются вокруг продольной оси.
2. Радиусы поперечных сечений не искривляются и не изменяют свою длину.
3. Расстояния между поперечными сечениями не меняются.
Опираясь на изложенные гипотезы можно заключить, что при чистом кручении круглого стержня в его поперечных сечениях отсутствуют нормальные напряжения, а касательные являются функцией от внутреннего усилия τ =f(Мt) (крутящего момента) и находятся по формуле: τ =(Мt /Iρ )ρ, где Iρ – полярный момент инерции сечения, ρ – радиус вектор (расстояние от центра тяжести сечения до точки в которой определяется напряжение). Обозначим отношение полярного момента инерции к расстоянию до наиболее удаленной от центра тяжести поперечного сечения точки через полярный момент сопротивления сечения Iρ / ρ max = Wρ . Тогда максимальное по модулю касательное напряжение можно найти как / τ / max = / М t / max / Wρ . Условие прочности при кручении имеет следующий вид: / τ / max = / М t / max / Wρ ≤ Rs , где Rs – расчетное сопротивление срезу. С помощью условия прочности можно определять допустимое значение крутящего момента и размеры поперечного сечения, также выполнять проверку прочности. Перемещением при кручении является угол закручивания поперечного сечения. Его находят как сумму интегралов от функции внутреннего усилия, отнесенного к жесткости стержня при кручении (
- крутильная жесткость). Интегрирование ведется в пределах грузового участка. 
Если в пределах грузового участка длиной 
внутреннее усилие Мt=const, то угол закручивания можно определить как 
. Также различают относительный угол закручивания 
. Расчет на жесткость производят с помощью условий жесткости, круг решаемых задач тот же, что и в расчете на прочность. Условия жесткости при кручении имеют вид: 
, 
. В квадратных скобках допустимые значения углов.
Пример выполнения индивидуального задания
Статически определимая задача
Дано: расчетное сопротивление сдвигу
, модуль сдвига
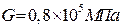, допустимый
угол закручивания 
.
Требуется: из условий прочности
и жесткости подобрать размеры поперечного сечения в трех вариантах: круглое сплошное сечение, трубу (α =dint /dext=0, 9), прямоугольное сечение (h/b=1). Выбрать выгодное с экономической точки зрения сечение.
Решение
1) Построение эпюры внутренних усилий (крутящих моментов)
Разобьем стержень на грузовые участки, пронумеруем сечения в начале и конце каждого участка. Стержень жестко защемлен с одного конца, с другого – конец свободный, поэтому опорные реакции (момент в заделке) определять не требуется. Запишем уравнения крутящих моментов на грузовых участках, рассматривая ту отсеченную часть, которая содержит свободный конец.
Мt, I=-М1+mx=-2+1, 5x – линейное уравнение, Мt, 1-1=-2кНм, Мt, 2-2=1кНм;
Мt, II=-М1-М2+m× 2=-2+3-1=0 – const, Мt, 3-3=Мt, 4-4=0;
Мt, III=-М1-М2+m× 2-М3=-2+3-1-2=-2 – const, Мt, 5-5=Мt, 6-6=-2;
Мt, IV=-М1-М2+m× 2-М3+М4=-2+3-1-2+3=1 – const Мt, 7-7=Мt, 8-8=1.
Построим эпюру крутящих моментов.
2) Построение эпюры φ ٭
Угол закручивания свободного конца
можно определить как сумму
.
Т.к. на всех грузовых участках
=const, то обозначим φ × =φ, ٭
помня о том, что геометрический
Эп. Мt[кНм] смысл интеграла это площадь, получим:
;
;
;
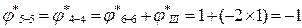Эп. φ ٭ 
Построим эпюру φ.٭
3) Расчет на прочность и жесткость. Подбор сечений
С помощью эпюры крутящих моментов определим опасное сечение. Это может быть сечение 1-1 или любое сечение в пределах третьего грузового участка, где / М t / max =2кНм. Запишем условие прочности / τ / max = / М t / max / Wρ ≤ Rs, приравняем максимальноепо модулю касательное напряжение к расчетному сопротивлению срезу, выразим требуемый для выполнения условия прочности полярный момент сопротивления сечения: Wρ тр= / М t / max / Rs =2/(80× 103)=25× 10-6м3= 25см3.
Величина требуемого полярного момента сопротивления сечения обеспечивает выполнение условия прочности, она зависит от максимального крутящего момента в опасном сечении и от расчетного сопротивления срезу. Величина требуемого полярного момента сопротивления сечения не зависит от формы поперечного сечения.
а) определим диаметр круглого сечения
Для круглого сечения полярный момент инерции Iρ =π d4/32, ρ max = d/2, тогда полярный момент сопротивления сплошного круглого сечения можно выразить через диаметр Wρ =Iρ / ρ max=(π d4/32)/d/2=π d3/16. Приравняем Wρ тр=π d3/16 и выразим диаметр d=(16Wρ тр/π)1/3=(16× 25/3, 14)1/3=5см. Вычислим с этим диаметром значение наибольшего по модулю касательного напряжения: / τ / max= / Мt / max / Wρ =2× 10-3/(3, 14× 53× 10-6/16)=81, 5МПа > 80МПа, очевидно, что имеет место перенапряжение, найдем процент перенапряжения, помня что допустимым является 5%: (81, 5-80) 100% / 80 = 1, 875% < 5% - допустимо. Определим полярный момент инерции Iρ =π d4/32=3, 14× 54/32=61, 3см4. Из условия прочности найден диаметр, теперь выполним проверку жесткости. Для этого найдем опасное сечение с помощью эпюры φ, ٭ им является сечение 1-1, где /φ ٭ /max=2. Запишем условие жесткости и с его помощью выполним проверку: 
Условие выполняется, окончательно принимаем d=5см. Построим эпюру касательных напряжений.
эп. τ [МПа]
 |
Определим площадь сплошного круглого сечения
А● = π d2/4=3, 14× 52/4=19, 6см2.
б) определим диаметр трубчатого сечения
Расчет выполняется аналогично предыдущему. Полярный момент инерции Iρ =π d4ext(1-α 4)/32, ρ max = dext/2, тогда полярный момент сопротивления трубы можно выразить через диаметр Wρ =Iρ / ρ max=π d3ext(1-α 4)/16. Приравняем Wρ тр=π d3ext(1-α 4)/16 и выразим диаметр dext=(16Wρ тр/π (1-α 4))1/3=(16× 25/3, 14(1-0, 94))1/3=7, 2см. Вычислим с этим диметром значение наибольшего по модулю касательного напряжения: / τ / max= / Мt / max / Wρ =2× 10-3/(3, 14× 7, 23× 10-6(1-0, 94)/16)=78, 2МПа < 80МПа.
Определим полярный момент инерциитрубчатого сечения по формуле, приведенной ранее Iρ =π d4ext(1-α 4)/32=3, 14× 7, 24(1-0, 94)/32=90, 7см4. Из условия прочности найден диаметр трубы, теперь выполним проверку жесткости: 
Условие выполняется, окончательно принимаем dext=7, 2см. Построим эпюру касательных напряжений.
эп. τ [МПа]
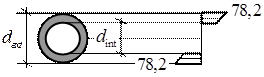Определим площадь трубчатого сечения
А○ = π d2ext(1-α 4)/4=3, 14× 7, 22(1-0, 94)/4=7, 7см2.
в) определим размеры прямоугольного сечения
При кручении прямоугольных сечений используют следующие геометрические характеристики. Момент инерции It=β hb3 имоментсопротивления Wt=α hb2, т.к в данном случае h/b=1 (α =0, 208; β =0, 141 – определяются по таблице, в зависимости от h/b), выразим высоту сечения через ширину и получим Wt=α b3. Приравняем Wtтр=α b3, выразим b=(Wt /α)1/3=(25/0, 208)1/3=4, 9см. Вычислим касательное напряжение: / τ / max= / Мt / max / Wt=2× 10-3/(0, 208× 4, 93× 10-6)=81, 7МПа > 80МПа, очевидно, что имеет место перенапряжение, найдем процент перенапряжения: (81, 7 - 80) 100% / 80 = 2, 1% < 5% - допустимо. Определим момент инерции при кручении It=β hb3=0, 141× 4, 94=81, 3см4. Из условия прочности найдены размеры сечения, теперь выполним проверку жесткости: 
Условие выполняется, окончательно принимаем h=b=4, 9см. Построим эпюру касательных напряжений.
эп. τ [МПа]
 |
Определим площадь прямоугольного сечения
= h× b=4, 92=24см2.
При h> b эпюра касательных напряжений в прямоугольном сечении будет иметь следующий вид.
эп. τ [МПа]
 |
Сравним площади поперечных сечений: = 24см2 > А● = 19, 6см2 > А○ = 7, 7см2 – наименьшей является площадь трубчатого поперечного сечения. С экономической точки зрения выгодным является использовать при кручении поперечное сечение в виде трубы.
|