Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

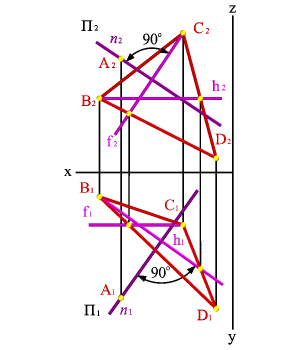Дано: плоскость ВСD и точка А. Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD. В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1 перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2 перпендикулярно фронтальной проекции фронтали f2, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.

20) многогранники. Их задание на чертеже. Точка и прямая на поверхности многогранника.

Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Классификация многогранников:

- выпуклые: правильные(тела Платона, тетраэдр, октаэдр), полувыпуклые(тела Архимеда), паралеаэдры(тела Фдорова);

- вогнутые: правильные(тела Пуансо), неправильные(призмы, пирамиды);

Призма – многогранник, в основании которого находится плоский n-угольник, а остальные грани явл. пар-ными линиями. Пирамида – многогранник, в основании которого находится поский n-угольник, а боковые грани явл. треугольник с общей вершиной.

Построение точек пересечения прямой с поверхностью многогранника сводится к построению линии пересечения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рис. 6.6 приведено построение проекций e1, e2 и f1, f2 точек пересечения прямой с проекциями m1 n1, m2 n2 с боковыми гранями пирамиды. Прямая MN заключена во вспомогательную фронтально-проецирующую плоскость T (T2). Горизонтальные проекции e1 и f1 искомых точек построены в пересечении прокции m1 n1 с горизонтальными проекциями 1131 и 3121 отрезков, по которым плоскость Т пересекает боковые грани пирамиды. Фронтальные проекции e2 и f2 определены по линиям связи.

.

21) пересечение многогранников плоскостью

Геометрическая фигура, получающаяся в результате пересечения

Многогранника плоскостью, называется сечением многогранника.

22) пересечение прямой с многогранником.

Алгоритм решения задачи:

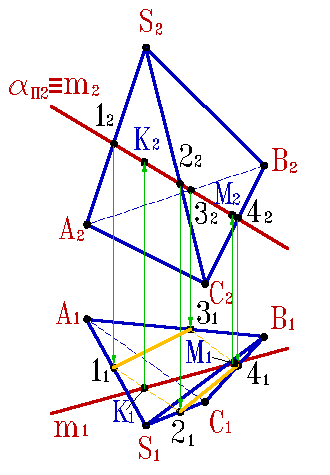1. Через заданную прямую m проводим вспомогательную секущую плоскость a (mÎ a).

2. Строим сечение многогранника с вспомогательной секущей плоскостью a.

3. Определить искомые точки К, М - пересечения полученного сечения с прямой m.

4. Определить видимость прямой по отношению к пирамиде.

Прямая пересекает многогранную поверхность в нескольких точках,

различных или совпадающих.

Если многогранник выпуклый, то существует 2 точки

пересечения прямой с многогранной поверхностью,

их называют точками встречи.

23) взаимное пересечение многогранников.

Сечение многогранника плоскостью можно построить двумя способами:

1. По точкам пересечения с плоскостью ребер многогранника. 2. По линиям пересечения граней многогранника с плоскостью.

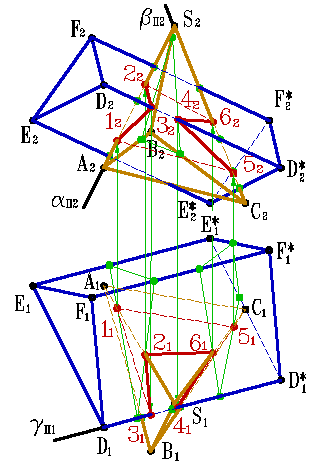Если проекция ребра одной из поверхностей не пересекает проекции грани другой, хотя бы на одной из проекций, то данное ребро не пересекает этой грани.

24) способы преобразования чертежа.

Цель способов преобразования чертежа - приведение геометрических фигур в частное (параллельное или проецирующее) положение относительно плоскостей проекций для обеспечения большей наглядности изображения и упрощения решения позиционных и метрических задач.

Сущность способа вращения; Сущность способа замены плоскостей проекций; Способ плоскостно-параллельного перемещения;

Способ совмещения;

25, 26) способ замены плоскостей. при сохранении неизменного положения фигуры в пространстве вводится новая плоскость проекций, перпендикулярная одной из основных плоскостей проекций; для получения новой проекции фигуры она ортогонально проецируется на введенную плоскость проекций.

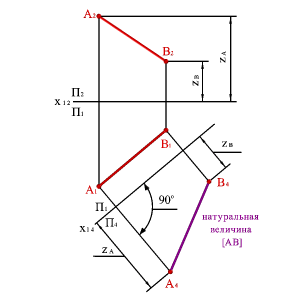
27, 28, 29) способ вращения.

: фигура приводится в частное положение относительно неизменной системы основных плоскостей проекций путем вращения вокруг некоторой оси.

Алгоритм графических построений:

Проведем ось вращения i через точку B. Ось i перпендикулярна П2;

Повернем отрезок AB до состояния параллельности оси проекций П1П2. Где A1'B1' - новая проекция AB;

Проводим вспомогательную линию на П2. Эта линия символизирует горизонтальную плоскость, в которой поворачивалась точка A;

Проводим линию связи и находим новую проекцию A2'B2' отрезка AB на П2;

A2'B2' - натуральная величина отрезка AB.

30, 31) способ плоско-параллельного перемещения.

методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях.

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.

показан комплексный чертеж прямой АВ. Прямая не параллельна ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций, например П2. Через произвольную точку А1, проводим прямую l1 параллельную оси П2/П1, и от этой точки на прямой откладываем отрезок, равный А1 В1. Из точки А1 проводим вертикальную линию связи, а из точки AT, — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А2'. Аналогично проведем вертикальную линию связи из точки В1 до пересечения с горизонтальной линией, проведенной из точки B2. Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В2'. После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П2, а значит, спроецировалась она на эту плоскость в натуральную величину.

32) способ совмещения.

Эффективным приёмом, упрощающим решение ряда задач, связанных с определением метрических характеристик плоских фигур, с построением в плоскости общего положения фигуры заданной формы и размеров, является поворот плоскости вокруг её следа до совмещения с плоскостью проекций. Этот способ преобразования чертежа, являющийся частным случаем вращения плоскости вокруг линии уровня, известен в начертательной геометрии как способ совмещения.

При совмещении за ось вращения принимается её горизонтальный или фронтальный след - нулевые горизонталь или фронталь. В результате поворота плоскости она совпадает (совмещается) с плоскостью проекций П1, если вращение осуществляется вокруг горизонтального следа плоскости, либо с П2 при вращении вокруг её фронтального следа. На рисунке показано совмещение плоскости общего положения Р с горизонтальной плоскостью проекций П1. Поворот произведён вокруг горизонтального следа Рh, в направлении от фронтальной плоскости проекций к зрителю. В положении совмещения с плоскостью П1 на плоскости Р окажутся две пересекающиеся прямые – след Рh и прямая Рv/, которая представляет собой след Рv, совмещённый с плоскостью П1. След Рh, как ось вращения, не меняет своего положения, точка пересечения следов Рх - точка схода следов, также не меняет своего положения. Поэтому для нахождения совмещённого положения плоскости достаточно найти совмещённое положение ещё одной точки (кроме Рх), принадлежащей фронтальному следу Рv – точки N. Эта точка опишет дугу окружности в пл. Q, перпендикулярной к оси вращения, центр этой дуги лежит в точке О – пересечения плоскости Q со следом Рh. Описывая из точки О дугу радиусом ОN в плоскости Q, мы получаем в пересечении этой дуги с Qh точку N′ на плоскости П1. Проведя через Рх и N′ прямую, получим Рv′. Так как отрезок РxN не изменяет своей величины при вращении плоскости, то, очевидно, точку N можно получить в пересечении Оh с дугой, описанной в пл. П1 из Рх радиусом РхN.

36) определение расстояния от точки до плоскости.

35) ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ДВУМЯ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ.

Это расстояние равно длине общего перпендикуляра MN к заданным прямым АВ и CD (рис. 10.6). Для определения его длины удобно, чтобы одна из прямых располагалась перпендикулярно плоскости проекций. Для этого надо последовательно ввести две новые плоскости проекций.

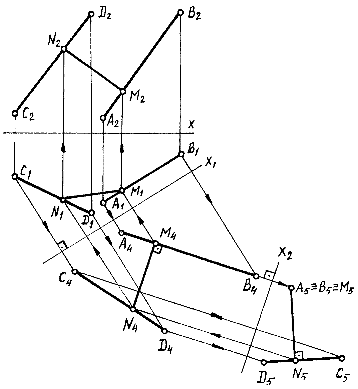
34) Определить расстояние между параллельными прямыми.

Для решения задачи необходимо выполнить две замены плоскостей проекций. Вначале прямые a и b необходимо сделать прямыми уровня. Для этого П4 необходимо расположить параллельно a1 и b1. Затем названные прямые необходимо расположить перпендикулярно П5. Расстояние между а5 и b5 будет натуральной величиной между параллельными прямыми a и b (рис. 6.2).

33) Определение расстояния от точки М до прямой ав общего положения.

Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую АВ. Отрезок [МN] спроецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой АВ. Составляем алгоритм решения: 1. Преобразовать прямую АВ в проецирующую прямую способом замены плоскостей проекций. 2. Построить проекцию отрезка [МN] на плоскость П5 АВ, длина которого М5N5 определяет искомое расстояние.

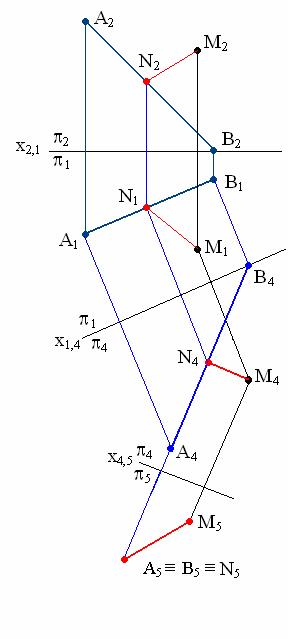Для преобразования прямой АВ общего положения в проецирующую выполнены две последовательные замены плоскостей проекций: вначале прямая АВ преобразована в линию уровня, затем линия уровня преобразована в проецирующую прямую. Построены проекций М4 и М5 точки М в системе П4/П5. Отрезок [М5N5] является искомым: [М5N5] [МN] и /М5N5/ = /МN/. На рис. 6.1 показано построение проекций [М4N4], [М1N1] и [М2М2] отрезка [МN] обратным преобразованием.

38) определение угла между параллельными прямыми.

При пересечении двух параллельных прямых третьей прямой, образуются восемь углов (рис.13), которые попарно называются:

1) соответственные углы (1 и 5; 2 и 6; 3 и 7; 4 и 8); эти углы попарно равны: (1 = 5; 2 = 6; 3 = 7; 4 = 8);

2) внутренние накрест лежащие углы (4 и 5; 3 и 6); они попарно равны;

3) внешние накрест лежащие углы (1 и 8; 2 и 7); они попарно равны;

4) внутренние односторонние углы (3 и 5; 4 и 6); их сумма равна 180° (3 + 5 = 180°; 4 + 6 = 180°);

5) внешние односторонние углы (1 и 7; 2 и 8); их сумма равна 180°(1 + 7 = 180°; 2 + 8 = 180°).

Углы с соответственно параллельными сторонами либо равны друг другу (если они оба острые, или оба тупые, 1 = 2, рис.14), либо их сумма равна 180° (3 + 4 = 180°, рис.15).

Углы с соответственно параллельными сторонами либо равны друг другу

(если они оба острые, или оба тупые, 1 = 2, рис.14)

, либо их сумма равна 180° (3 + 4 = 180°, рис.15).

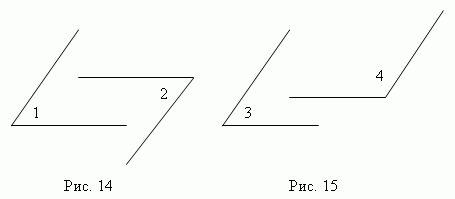
39) углы между двумя скрещивающимися прямыми.

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

40) определение угла между прямой и плоскостью. Угол между прямой и проекцией этой прямой на плоскость называется углом между прямой и плоскостью.

угол между прямой и плоскостью можно считать по формуле:

sinφ =∣ cosγ ∣ =(|Ap1+Bp2+Cp3|)/(√ A2+B2+C2)(√ p21+p22+p23)

41) определение угла между плоскостями.

Нарисуем нормальные векторы и плоскостей и с началами в точке М.

В каждой из плоскостей проведем перпендикуляры и к линии пересечения.

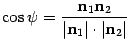
42) кривые линии. Проекции плоских кривых.

Кривые линии: плоские (гипербола, эллипс, парабола), пространственные алгебраические, трансцендентные, коробовые, лекальные, циклические, циркульные, гладкие, закономерные, эквитангентные, эквидистантные.

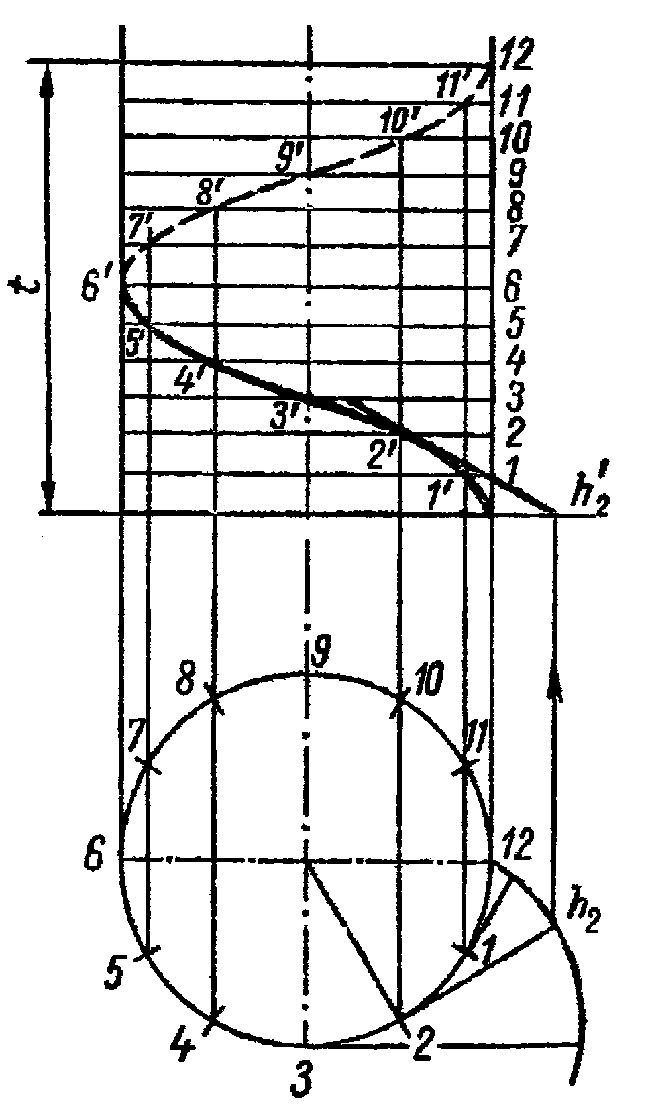43) винтовые линии. 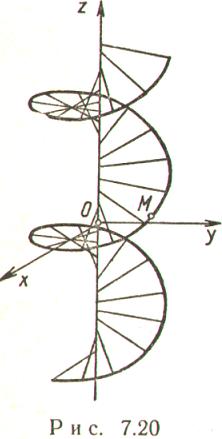Винтовая линия - линия, описываемая точкой M, которая вращается с постоянной угловой скоростью w вокруг неподвижной оси (Oz) и одновременно перемещается поступательно с постоянной скоростью v вдоль этой оси.

Построение цилиндрической винтовой линии.

1. Делим окружность на равные части. 2. Делим шаг винтовой линии t (заданный) на такое же количество равных частей. 3. Пересечение одноименных фронтальных и горизонтальных линия дает точки винтовой линии.

44) КОНИЧЕСКАЯ ВИНТОВАЯ ЛИНИЯ.

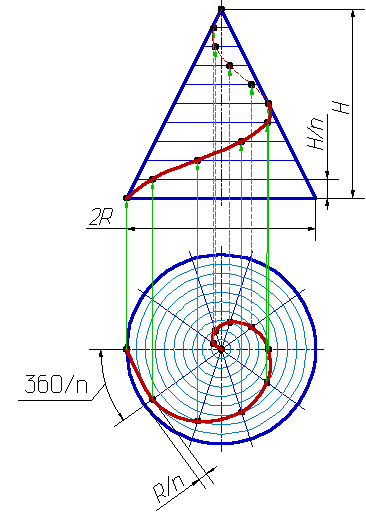Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса. Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда - одна из замечательных плоских кривых линий.

45) Поверхности. Их классификация.

Поверхности – непрерывное множество точек, если между координатами точек может быть установлена зависимость уравнения вида F(x; y; z)=0 рассматривают как совокупность последовательных положений перемещающейся линии.

1) По способу образования: кинематические; каркасные; вращения; винтовые.

2) По виду математического уравнения: алгебраические; трансцендентные.

3) По типу образующей: линейчатые; не линейчатые.

4) По числу направляющих: с тремя направляющими; с семью направляющими; с двумя и одной плоскостью.

5) По виду образующей: с образующей постоянного вида; с образующей переменного вида.

6) По развёртывости: развёртываемые; не развёртываемые.

7) По гладкости: гладкие; не гладкие.

8) По способу задания: аналитические; графические.

46) способы задания поверхностей.

Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать внутренние свойства поверхности. При проектировании поверхностей технических форм и их воспроизведении на станках с программным управлением используются совместно графические и аналитические способы задания поверхностей.

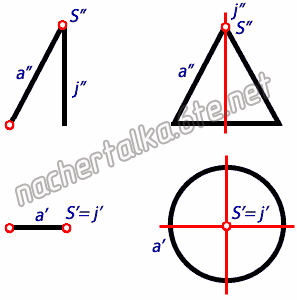Графический способ задания кинематической поверхности предполагает задание на ортогональном чертеже элементов определителя поверхности – независимых условий, однозначно определяющих эту поверхность.

I2 - поверхность вращения и ось вращения.

L - образующая имеет множество положений.

47) поверхности вращения.

Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i.

Геометрическая часть определителя состоит из двух линий: образующей m и оси i.

Алгоритмическая часть включает две операции:

1. на образующей m выделяют ряд точек A, B, C, …F.

2. каждую точку вращают вокруг оси i.

Из закона образования поверхности вращения вытекают два основных свойства:

Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.

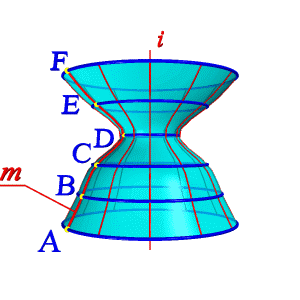
Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.

49) Линия и точка, принадлежащие поверхности.