
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение формата микрокоманды
|
|
На разрядность полей микрокоманды влияют следующие параметры:
- количество различных микроопераций, формируемых УА, в конечном итоге определяет (с учетом выбранного способа кодирования) длину поля микроопераций;
- количество различных логических условий определяет длину поля х;
- количество вершин ГСА связано с общим числом микрокоманд, а следовательно, с объемом памяти микропрограмм и разрядностью поля адреса микрокоманды.
Множество микроопераций Y, используемых в заданной ГСА Y={yl, y2, …..., y13} мощность множества |Y| = 13. При горизонтальном кодировании поле микроопераций будет занимать 13 разрядов. Вертикальный способ кодирования микроопераций к заданной ГСА неприменим, поскольку ГСА содержит вершины с двумя и тремя микрооперациями. Попробуем реализовать разбиение множества Y на подмножества несовместимых микроопераций. Воспользуемся методом прямого включения, учитывая, что отношение совместимости задано на самой ГСА. Строго говоря, следовало бы построить матрицу совместимости микроопераций, но в рассматриваемом примере небольшой размер алгоритма позволяет определять отношение совместимости непосредственно по ГСА.
На сколько подмножеств следует разбивать исходное множество? По меньшей мере, на s = 3 в нашем случае. Образуем три подмножества — Y1, Y2, YЗ и разместим в них микрооперации операторной вершины, имеющей s микроопераций. Если в ГСА таких вершин несколько— выберем любую из них.
Y1 ={y1}, Y2={y4}, Y3={y7}.
Теперь разместим по множествам микрооперации следующей вершины, содержащей (в нашем случае) три микрооперации:
Y1 ={y1}, Y2={y4, y5}, Y3={y7, y8}.
Заметим, что первая микрооперация второй рассматриваемой вершины совпадает с первой микрооперацией первой вершины. Она уже присутствует в множестве Y1 (y1 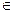 Y1), поэтому не включается вторично. Наконец, разместим микрооперации третьей " тройной" вершины:
Y1), поэтому не включается вторично. Наконец, разместим микрооперации третьей " тройной" вершины:
Y1 ={y1, y11}, Y2={y4, y5, y12}, Y3={ y7, y8, y13}.
Теперь нераспределенными остались микрооперации (некоторые) " двойных" и " одинарных" вершин. Вершина (у2, у6)— обе микрооперации несовместимы с уже распределенными, поэтому могут располагаться произвольно, лишь бы они находились в разных подмножествах:
Y1 ={y1, y11, y2}, Y2={y4, y5, y12, y6}, Y3={ y7, y8, y13}.
Вершина (у2, y9) – y9 нельзя помещать в Y1, поскольку совместимая с ней y2 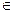 Y1. Подмножества лучше заполнять равномерно, поэтому разместим у9 в Y3:
Y1. Подмножества лучше заполнять равномерно, поэтому разместим у9 в Y3:
Y1 ={y1, y11, y2}, Y2={y4, y5, y12, y6}, Y3={ y7, y8, y13, y9}.
Остались две нераспределенные микрооперации - у3 и у10, первая из которых совместима с у5, поэтому ее нельзя помещать в Y2 а вторая несовместима ни с какими другими и может размещаться произвольно. Поместим их в множество, имеющее пока наименьшую мощность — Y1:
Y1 ={y1, y11, y2, y3, y10}, Y2={y4, y5, y12, y6}, Y3={ y7, y8, y13, y9}.
Все 13 микроопераций распределились по трем подмножествам, при этом выполняются условия (4.8) (т. е. имеет место разбиение исходного множеств; Y), однако УА обычно должен вырабатывать еще одну микрооперацию, свидетельствующую об окончании выполнения алгоритма и предназначенную для использования не в ОА, а в управляющем автомате верхнего уровня иерархии. Назовем эту микрооперацию yk и включим в произвольное множество (например, в Y2), поскольку она, естественно, несовместима ни с одной микрооперацией. Итак, имеем следующее распределение:
Y1 ={y1, y11, y2, y3, y10}, Y2={y4, y5, y12, y6, yk}, Y3={ y7, y8, y13, y9}.
Для кодирования элементов каждого из трех подмножеств потребуется по три двоичных разряда. Может показаться, что для Y3 хватит и двух, ведь
|Y3| = 4 = 22, однако следует учесть, что в каждом подмножестве необходимо предусмотреть один код для случая отсутствия микрооперации из этого подмножества в микрокоманде. Оптимальным разбиением исходного множества будет такое, когда  |Yi| = 2r -1, где r — натуральное число.
|Yi| = 2r -1, где r — натуральное число.
В подмножестве Y3 всего одна " лишняя" микрооперация, а среди кодов Y1 и Y2 есть свободные. Попробуем перенести одну из микроопераций из Y3 в другое подмножество, сохраняя, естественно, требование к попарной несовместимости всех микроопераций одного подмножества. Очевидно, первые три элемента подмножества Y3 нельзя перенести в другое, т. к. они являются микрооперациями из " тройных" вершин. Зато микрооперация у9 совместима только с y2 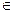 Y1, поэтому у9 можно перенести в Y2 Окончательно получим, предварительно упорядочив элементы подмножеств в порядке возрастания индексов:
Y1, поэтому у9 можно перенести в Y2 Окончательно получим, предварительно упорядочив элементы подмножеств в порядке возрастания индексов:
Y1 ={y1, y2, y3, y10, y11}, Y2={y4, y5, y6, y9, y12, yk}, Y3={ y7, y8, y13}.
Теперь мы можем определить размеры полей микрокоманды. Поле микроопераций будет состоять из трех подполей — Y1, Y2, YЗ (назовем их по именам соответствующих подмножеств), размером в 3, 3 и 2 двоичных разрядов соответственно.
Поле номера условия х должно содержать номер одного из двух логических условий — x1, х2 (один разряд?), однако для повышения гибкости процесса микропрограммирования удобно иметь возможность выбирать еще и тождественно истинное и тождественно ложное условия. Итак, поле х занимает два разряда.
 Наконец, поле адреса определяется объемом памяти микропрограмм. Если в нашем примере мы будем считать, что разрабатываем УА только для реализации микропрограммы рис. 4.14, а она содержит 8 вершин, не считая начальной, конечной и условных, количество микрокоманд (каждая микрокоманда — ячейка памяти, имеющая свой адрес), выдаваемых УА, будет никак не менее 8, а реально — (1, 2,..., 1, 3) х 8, то для поля адреса в микрокоманде следует отвести 4 разряда (24 = 16 > 1, 3 х 8»11).
Наконец, поле адреса определяется объемом памяти микропрограмм. Если в нашем примере мы будем считать, что разрабатываем УА только для реализации микропрограммы рис. 4.14, а она содержит 8 вершин, не считая начальной, конечной и условных, количество микрокоманд (каждая микрокоманда — ячейка памяти, имеющая свой адрес), выдаваемых УА, будет никак не менее 8, а реально — (1, 2,..., 1, 3) х 8, то для поля адреса в микрокоманде следует отвести 4 разряда (24 = 16 > 1, 3 х 8»11).
В поле адреса будет располагаться адрес памяти — двоичный номер ячейки, а в полях Yi и х — коды микроопераций и логических условий. Окончательно формат микрокоманды будет иметь вид, приведенный на рис. 4.15.