
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача минимизации затрат на проект
|
|
До сих пор мы рассматривали сетевые модели комплексов работ, в которых подлежал контролю лишь один параметр — время. Очевидно, что такой подход существенно обедняет процесс управления проектами. Для устранения этого недостатка введем в рассмотрение второй параметр — стоимость выполнения работ, а на сети поставим задачу минимизации затрат на проект.
Пусть дан граф G (N, А), представляющий собой сетевую модель комплекса работ. Поставим в соответствие каждой работе сети два параметра — продолжительность выполнения (tij) и затраты на выполнение (pij).Очевидно, что затраты находятся в обратной зависимости от продолжительности, т. е. чем раньше надо закончить работу, тем больше средств придется в нее вложить (оплата труда исполнителей, затраты на оборудование и пр.). Эта зависимость имеет сложный характер, и для упрощения решения задачи ее следует аппроксимировать прямой, график которой представлен на рис. 4.15.
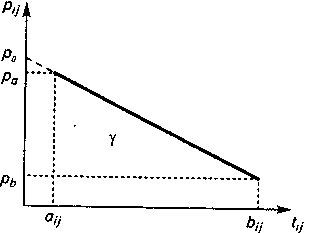
Рис. 4.15. Зависимость затрат на работу от ее продолжительности:
bij - нормальная продолжительность работы; aij - ускоренная продолжительность работы; рb -затраты при нормальной продолжительности; рa - затраты при ускоренной продолжительности; aij £ tij £ bij
Угол наклона прямой (без учета знака) характеризует интенсивность нарастания затрат, т. е. приращение затрат, необходимое для сокращения длительности работы на единицу: tg g = cij = (ра —рb)/(bij - аij). Приращение затрат — величина, обратная эффективности вложения средств в сокращение длительности работы: eij = 1/cij. Другими словами, вложение дополнительных средств наиболее эффективно в работы, которые имеют минимальные значения угловых коэффициентов сij. Затраты на выполнение работы в общем случае определяются по формуле:
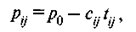
где р0 — условная точка пересечения прямой затрат с осью ординат.
Суммарные затраты на выполнение всего проекта, которые следует минимизировать, тогда могут быть определены следующим образом: 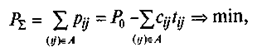
где Р0 - суммарные условные затраты (константа для данного проекта).
Задача минимизации затрат на проект — это оптимизационная задача, которая ставится как задача параметрического линейного программирования:
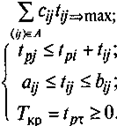
Для ряда допустимых значений продолжительности критического пути как параметра требуется найти наборы значений переменных /. и tr, минимизирующие затраты на выполнение проекта. Графически оптимальное решение имеет вид кривой, ограничивающей снизу область допустимых решений задачи. Это кривая затрат на проект (рис. 4.16).
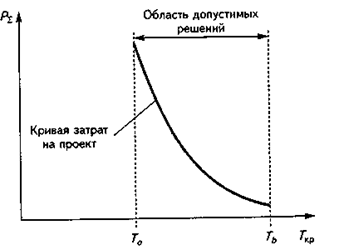
Рис. 4.16. Графическая интерпретация решения задачи
Прямая постановка задачи формулируется следующим образом: в какие конкретно работы нужно вложить дополнительные средства и насколько следует сократить их продолжительность, чтобы проект бьш завершен к заданному сроку, а суммарные вложения были бы при этом минимальны. Обратная постановка задачи сводится к тому, как Распределить между работами ограниченные дополнительные инвестиции, чтобы достичь максимального сокращения срока завершения проекта. Решение и той и другой задачи возможно методами линейного программирования, но существует более быстрый и эффективный алгоритм, использующий сетевую постановку задачи. Это алгоритм Форда—Фалкерсона. Поставленная задача имеет тривиальное решение. Действительно, для сокращения срока выполнения проекта необходимо вкладывать средства исключительно в критические работы, предварительно проранжировав их в порядке возрастания угловых коэффициентов (коэффициентов нарастания затрат). Однако на практике тривиальные решения встречаются нечасто. И при решении этой задачи может случиться, что в результате сокращения критического пути в сети появятся новые второй, третий и т. д. критические пути и использование описанного выше примитивного алгоритма окажется чрезвычайно затруднительным. Именно на такие сложные случаи рассчитан алгоритм Форда-Фалкерсона.
Контрольные вопросы и задания
1. Дайте определение понятия «инновационный проект».
2. По каким признакам классифицируются инновационные проекты?
3. Перечислите состав и содержание основных этапов разработки инновационного проекта.
4. Какие методы используются для календарного планирования работ по проекту?
5. В чем состоит порядок сетевого планирования проекта?
6. Назовите основные элементы сетевого графика.
7. Перечислите параметры работ и событий сетевого графика и назовите методы их расчета.
8. В чем состоит различие системы PERT и метода PERT/Costl
9. Опишите содержание и задачи систем планирования и управления проектами GERT, CPM/MRP.
10. Назовите основных участников проектов и формы координации их деятельности в управлении проектами.
11. На рис. 4.17 показана сетевая модель проекта, значения продолжительности выполнения работ которого случайные величины, заданные трехоценочным способом в табл. 4.6. Требуется выполнить расчет временных характеристик проекта методом PERTH определить, к какому сроку будет завершен проект с вероятностью: а) 35%; б) 50%; в) 84%; г) 96, 5%; какова вероятность завершения проекта к срокам: а) 80, 5 дня; б) 79 дней; в) 83, 5 дня.
Таблица 4.6
| Код работы | Оценка длительности работы, дней | Код работы | Оценка длительности работы, дней | ||||
| aij | mij | bij | aij | mij | bij | ||
| 1-2 | 7-9 | ||||||
| 1-4 | 9-11 | ||||||
| 2-3 | 10-12 | ||||||
| 2-5 | 11-12 | ||||||
| 4-6 | 11-14 | ||||||
| 4-7 | 11-15 | ||||||
| 5-6 | 12-13 | ||||||
| 6-8 | 12-14 | ||||||
| 6-9 | 13-14 | ||||||
| 6-10 | 14-15 |
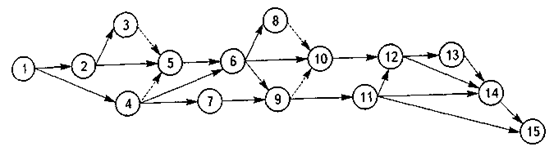
Рис. 4.17. Исходная сетевая модель для расчетов