Частные положения прямой в пространстве

ДОКЛАД

Точка, прямая и плоскость на комплексном чертеже

Работу выполнила студентка Макаренко Л.О.

Курс, группа, специальность 2курс, 221 группа, управление качеством

Преподаватель Нестеренко А.Г.

Краснодар 2012

Способы задания точки и прямой на комплексном чертеже

Точка, как математическое понятие, не имеет размеров. Очевидно, если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.

В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку будем принимать шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.

Прямая на комплексном чертеже может быть задана проекциями прямой; проекциями двух точек, принадлежащих прямой; проекциями отрезка прямой.

Свойства прямой на комплексном чертеже

1. Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая прямая может быть задана проекциями двух ее точек. Прямую на комплексном чертеже можно задать и ее проекциями.

2. Всякая непрофильная прямая вполне определяется двумя своими проекциями, для определения же профильной прямой необходимо задать на проекциях прямой проекции ее двух точек

3. Чтобы задать на одной профильной прямой какую-нибудь точку, достаточно задать ее проекции на одноименных проекциях данной прямой.

4. Для деления данного отрезка в данном отношении достаточно разделить в этом отношении одну из проекций данного отрезка, а затем спроецировать делящую точку на другую проекцию отрезка.

Частные положения прямой в пространстве

На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.

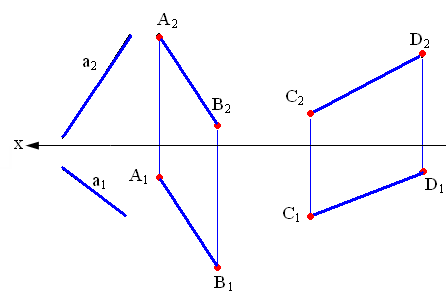
Рис. 2.1. Прямые общего положения

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.

Прямые, параллельные плоскостям проекций

1. Горизонтальная прямая h (рис. 2.2) - горизонталь

Горизонтальная прямая - это прямая, параллельная горизонтальной плоскости проекций π 1.

Так как все точки этой прямой равноудалены от плоскости проекций π 1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π 1 проецируются без искажения отрезок прямой АВ (А1В1=АВ) и углы наклона прямой к плоскостям проекций π 2 и π 3 (углы β ° и γ °).

2. Фронтальная прямая f (рис. 2.3) - фронталь

Фронтальная прямая - это прямая параллельная фронтальной плоскости проекций p2.

Так как все точки этой прямой равноудалены от плоскости проекций π 2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π 2 проецируются без искажений отрезок этой прямой CD (C2D2+CD) и углы наклона прямой к плоскостям проекций π 1 и π 3 (углы α ° и γ °)

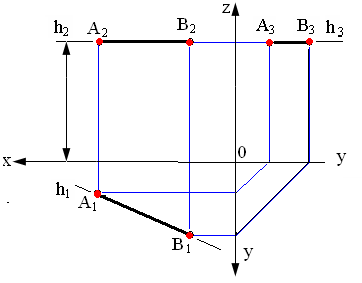
Рис. 2.2. Горизонтальная прямая на комплексном чертеже

3. Профильная прямая p (рис. 2.4)

Профильная прямая - это прямая, параллельная профильной плоскости проекций π 3

Так как все точки этой прямой равноудалены от плоскости проекций π 3 (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций p3 проецируется без искажения отрезок этой прямой EF (E3F3=EF) и углы наклона прямой к плоскостям проекций π 1 и π 2 (углы α ° и β °).

Прямые, принадлежащие плоскостям проекций

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

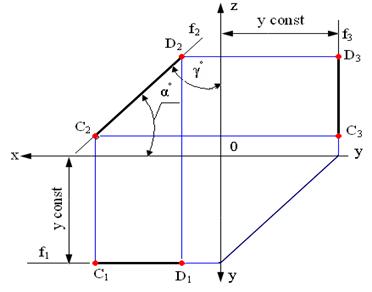
Рис. 2.3. Изображение фронтальной прямой

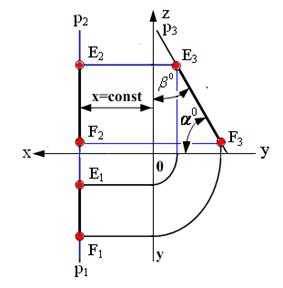
Рис. 2.4. Изображение профильной прямой

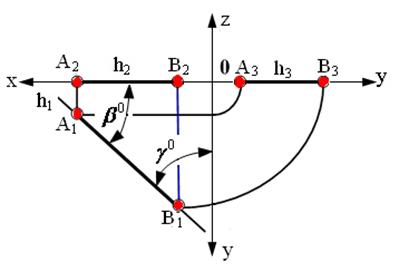
Рис. 2.5. Изображение прямой, принадлежащей горизонтальной плоскости проекций

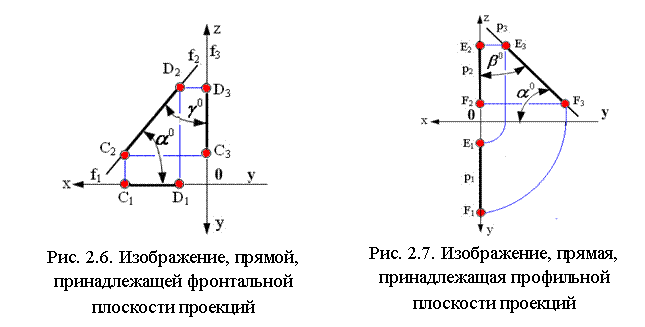
На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).

Прямые, перпендикулярные плоскостям проекций

Проецирующие прямые

На рис. 2.8, 2.9 и 2.10 показаны прямые на комплексном чертеже, перпендикулярные соответственно горизонтальной, фронтальной и профильной плоскостям проекций.

Прямая, перпендикулярная горизонтальной плоскости проекций - горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π 1 в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).

Прямая, перпендикулярная фронтальной плоскости проекций - фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π 2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).

Прямая, перпендикулярная профильной плоскости проекций - профильно-проецирующая прямая. Эта прямая проецируется на плоскость π 3 в точку, а ее фронтальная проекция перпендикулярна оси Z.

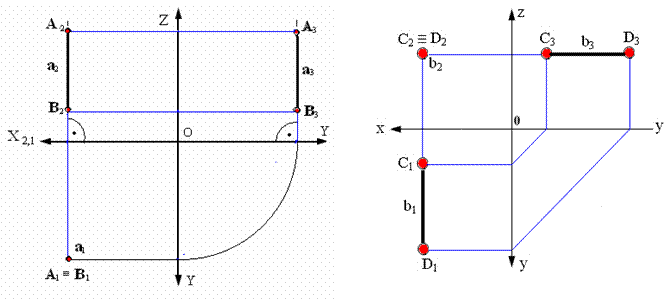
Рис. 2.8. Прямая, перпендикулярная Рис. 2.9. Прямая, перпендикулярная