
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Восстановление утраченных межевых знаков
|
|
Восстановление утраченных межевых знаков на местности выполняется по методикам, приведенным в разделе 4.5.3 и соответствующим вынесению в натуру проекта территориального землеустройства или земельных участков. Исходными данными для выполнения такого вида работ являются пункты геодезического обоснования и координаты утраченных межевых знаков, которые имеются в реестре объектов недвижимости.
Подготовка данных для восстановления межевого знака на местности относительно исходных пунктов геодезического обоснования в наиболее распространенном методе полярных координат выполняется по алгоритму, изложенному в разделе 4.5.3.2 (см. формулы (4.71) и (4.76)).
При выполнении подобного вида работ актуальным является рассмотрение вопроса, насколько точно будет восстановлен межевой знак относительно своего первоначального положения. Средняя квадратическая ошибка восстановления межевого знака в первую очередь обусловлена инструментальной точностью используемого электронного тахеометра. Например, при точностях mβ = 2'' и mL = 1 cм и длине линии от исходного до восстанавливаемого межевого знака L = 100 м, на основании формулы (4.98) имеем
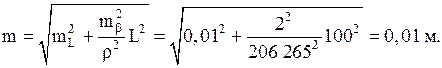 (4.113)
(4.113)
Для геометрической интерпретации полученных результатов рассмотрим эллипс ошибок, полуоси которого определяются элементами формулы (4.113). Эллипс ошибок – это двухмерный интервал, который определяет зону расхождения между восстановленным межевым знаком и его первоначальным положением.
Например, если в реестре объектов недвижимости координаты утраченного межевого знака составляли X = 45, 514 м и Y = 57, 180 м и по отношению к координатным осям восстанавливаемый межевой знак располагается так, как показано на рис. 4.74, то размерности эллипса ошибок будут иметь следующие значения:
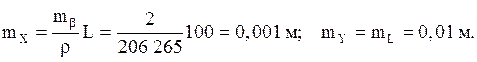
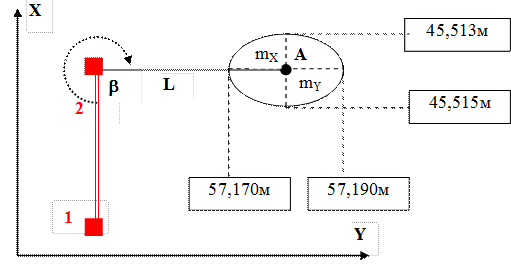
Рис. 4.74. Диапазон возможного расхождения между восстановленным
межевым знаком и его первоначальным положением
Следовательно, восстановленный межевой знак относительно своего первоначального положения будет находиться в двухмерном диапазоне, показанном на рис. 4.74.
Отметим, что эта ситуация характерна только для варианта, когда исходный пункт геодезического обоснования является безошибочным. Однако, исходя из теории, изложенной в разделе 4.3, исходная геодезическая сеть характеризуется матрицей весовых коэффициентов, определяемой уравнением (4.2.6). Поэтому каждый исходный пункт характеризуется своим эллипсом ошибок, размеры которого определяются формулой (4.33). Предположим, что исходным пунктом для восстановления межевого знака на местности является пункт 2 геодезической сети 4-го класса, изображенной на рис. 4.27. Средняя квадратическая ошибка этого пункта на основании матрицы весовых коэффициентов (см. табл. 4.23) составляет
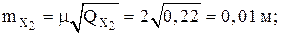
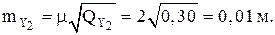
В этом случае средняя квадратическая ошибка для определения размеров эллипса ошибок восстанавливаемого межевого знака будет вычисляться по следующей формуле:
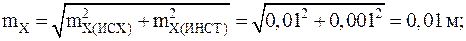
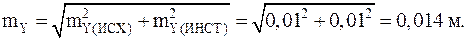
Следовательно, с учетом ошибок исходных данных диапазон возможного несовпадения восстановленного межевого знака с его первоначальным положением может быть намного больше (рис. 4.75).
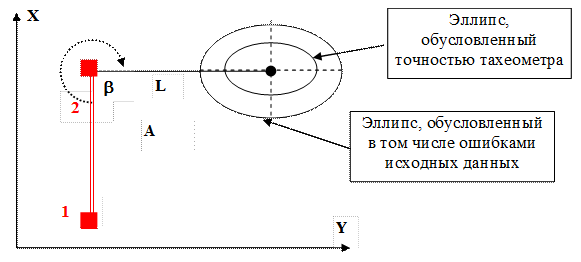
Рис. 4.75. Диапазон возможного расхождения между восстановленным межевым знаком и его первоначальным положением с учетом
ошибок исходных данных
Поэтому при восстановлении желательно использовать тот исходный пункт геодезического обоснования, который был исходным при первоначальной разбивке проекта территориального землеустройства. В этом случае ошибки исходных данных, даже самые большие, не влияют на положение восстанавливаемого межевого знака.