
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение. Стати́стика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных)
|
|
Стати́ стика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных;
Статистика разрабатывает специальную методологию исследования и обработки материалов: массовые статистические наблюдения, метод группировок, средних величин, индексов, балансовый метод, метод графических изображений и другие методы анализа статистических данных.
Статистика состоит из трёх разделов:
1. сбор статистических сведений, то есть сведений, характеризующих отдельные единицы каких-либо массовых совокупностей;
2. статистическое исследование полученных данных, заключающееся в выяснении тех закономерностей, которые могут быть установлены на основе данных массового наблюдения;
3. разработка приёмов статистического наблюдения и анализа статистических данных. Последний раздел, собственно, и составляет содержание математической статистики
Для записи результатов большого количества однотипных измерений удобно использовать таблицы. С их помощью удается избежать ненужной многократной записи обозначения измеряемой величины, единиц измерения, используемых множителей и т.п. В таблицы, помимо экспериментальных данных, могут быть сведены промежуточные результаты обработки этих данных. Например, Температурная зависимость удельного сопротивления платиновой проволоки
| Номер измерения | I, мА | V, мВ | UT, мВ | T, К | ρ, 10-7 Ом· м |
| 1, 0 | 2, 78 | 1, 02 | |||
| 1, 0 | 2, 83 | 0, 20 | 1, 04 | ||
| … | … | … | … | … | … |
Более наглядными, чем таблицы, являются графики зависимостей исследуемых физических величин. Графики дают визуальное представление о связи между величинами, что крайне важно при интерпретации полученных данных, так как графическая информация легко воспринимается, вызывает больше доверия, обладает значительной емкостью. На основе графика легче сделать вывод о соответствии теоретических представлений данным эксперимента.
Познакомимся с некоторыми характерными особенностями любых измерений.
Измерение – это нахождение числового значения физической величины опытным путем с помощью средств измерений (линейки, вольтметра, часы и т.д.).
Измерения могут быть прямыми и косвенными.
Прямое измерение – это нахождение числового значения физической величины непосредственно средствами измерений. Например, длину – линейкой, атмосферное давление- барометром.
Косвенное измерение – это нахождение числового значения физической величины по формуле, связывающей искомую величину с другими величинами, определяемыми прямыми измерениями. Например сопротивление проводника определяют по формуле R=U/I, где U и I измеряются электроизмерительными приборами.
Рассмотрим пример измерения.

Измерим напряжение в цепи вольтметром (цена деления 1В). Можно лишь утверждать, что напряжение составляет величину примерно 55В. Ширина интервала “неизвестности составляет 1В, те есть равна цене деления. Замена линейки более чувствительным прибором, снизит этот интервал, что приведет к повышению точности измерения. В нашем примере точность измерения не превышает 1В.
Поэтому измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный. Неопределенность в измерении характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения.
Перечислим некоторые из причин, приводящих к появлению погрешностей.
1. Ограниченная точность изготовления средств измерения.
2. Влияние на измерение внешних условий (изменение температуры, колебание напряжения …).
3. Действия экспериментатора (запаздывание с включением секундомера, различное положение глаза…).
4. Приближенный характер законов, используемых для нахождения измеряемых величин.
Перечисленные причины появления погрешностей неустранимы, хотя и могут быть сведены к минимуму. Для установления достоверности выводов, полученных в результате научных исследований существуют методы оценки данных погрешностей.
Погрешности, возникающие при измерениях делятся на систематические и случайные.
Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней.
Причины возникновения систематических погрешностей:
1) несоответствие средств измерения эталону;
2) неправильная установка измерительных приборов (наклон, неуравновешенность);
3) несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают;
4) несоответствие измеряемого объекта с предположением о его свойствах (наличие пустот и т.д).
Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.
Для количественной оценки качества измерений вводят понятия абсолютной и относительной погрешностей измерений.
Как уже говорилось, любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:
Апр- DА < Аист < Апр+ DА
Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. Апр – значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.
Но для оценки качества измерения необходимо определить относительную погрешность e.
e= DА/Апр или e= (DА/Апр)*100%.
Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.
Погрешности средств измерений называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки. Обычно довольствуются о допустимых инструментальных погрешностях, сообщаемых заводом изготовителем в паспорте к данному прибору. Эти допустимые погрешности регламентируются ГОСТами. Это относится и к эталонам. Обычно абсолютную инструментальную погрешность обозначают D иА.
Если сведений о допустимой погрешности не имеется, то в качестве этой погрешности можно принять половину цены деления.
Стрелочные электроизмерительные приборы по допустимым значениям погрешностям делятся на классы точности, которые обозначены на шкалах приборов числами 0, 1; 0, 2; 0, 5; 1, 0; 1, 5; 2, 5; 4, 0. Класс точности gпр прибора показывает, сколько процентов составляет абсолютная погрешность от всей шкалы прибора.
gпр = (DиА/Амакс)*100%.
Например абсолютная инструментальная погрешность прибора класса 2, 5 составляет 2, 5% от его шкалы.
Если известен класс точности прибора и его шкала, то можно определить абсолютную инструментальную погрешность измерения
DиА=(gпр * Амакс)/100.
Для повышения точности измерения стрелочным электроизмерительным прибором надо выбирать прибор с такой шкалой, чтобы в процессе измерения располагались во второй половине шкалы прибора.
Погрешность отсчета получается от недостаточно точного отсчитывания показаний средств измерений.
В большинстве случаев абсолютную погрешность отсчета принимают равной половине цены деления. Исключения составляют измерения стрелочными часами (стрелки передвигаются рывками).
Абсолютную погрешность отсчета принято обозначать DоА
При выполнении прямых измерений физической величины А нужно оценивать следующие погрешности: DиА, DоА и DсА (случайную). Конечно, иные источники ошибок, связанные с неправильной установкой приборов, несовмещение начального положения стрелки прибора с 0 и пр. должны быть исключены.
Полная абсолютная погрешность прямого измерения должна включать в себя все три вида погрешностей.
Если случайная погрешность мала по сравнению с наименьшим значением, которое может быть измерено данным средством измерения (по сравнению с ценой деления), то ее можно пренебречь и тогда для определения значения физической величины достаточно одного измерения. В противном случае теория вероятностей рекомендует находить результат измерения как среднее арифметическое значение результатов всей серии многократных измерений, погрешность результата вычислять методом математической статистики.
Окончательный результат измерения физической величины А следует записывать в такой форме;
А=Апр + DА, e= (DА/Апр)*100%.
Апр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. DА- полная абсолютная погрешность прямого измерения.
Абсолютную погрешность обычно выражают одной значащей цифрой.
Пример: L=(7, 9 + 0, 1) мм, e=13%.
При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Хпр, пользуясь формулами, приведенными в таблице (без доказательств).
Абсолютную погрешность определяется по формуле DХ=Хпр*e,
Где e выражается десятичной дробью, а не в процентах.
Окончательный результат записывается так же, как и в случае прямых измерений.
| Вид функции | Формула |
| Х=А+В+С | 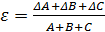
|
| Х=А-В | 
|
| Х=А*В*С | 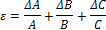
|
| Х=Аn | 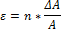
|
| Х=А/В | 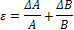
|
Х= 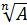
| 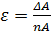
|