
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа №3.
|
|
1. Цель работы:
1.1 Ознакомление с алгоритмом метода Эйлера и Рунге – Кутта.
1.2 Набор и редактирование программ в системе MATLAB.
2 Содержание отчета:
2.1 Описание методов решения ODE;
2.2 Программы алгоритмов методов Эйлера и Рунге - Кутта;
2.3 Результаты счета.
3. Описание решения дифференциального уравнения
Обыкновенным дифференциальным уравнением называется выражение
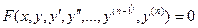 , (1)
, (1)
где 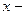 независимая переменная;
независимая переменная;
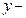 искомая функция (от
искомая функция (от  );
);
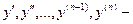 производные порядка 1, 2, …, n-1, n.
производные порядка 1, 2, …, n-1, n.
Порядок старшей производной, входящей в уравнение (1), называется порядком дифференциального уравнения.
Функция 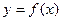 называется решением уравнения (1), если при подстановке ее в (1) последнее обращается в тождество.
называется решением уравнения (1), если при подстановке ее в (1) последнее обращается в тождество.
При нахождении частного решения необходимо указать начальные условия, а именно, задать значения 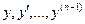 при
при 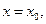 т.е.
т.е.
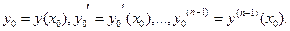 (2)
(2)
Уравнение (1) называется разрешенным относительно старшей производной, если оно имеет вид
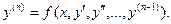 (3)
(3)
Уравнение (3) сводится к системе n обыкновенных дифференциальных уравнений первого порядка заменой 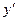 на неизвестную функцию
на неизвестную функцию 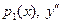 на
на  на
на 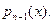 Таким образом, имеем:
Таким образом, имеем:


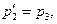 (4)
(4)
……….

причем
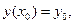
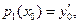
 ...
... 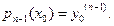
Во многих случаях приходится иметь дело с уравнениями, общее решение которых не выражаются в аналитическом виде. Поэтому возникает необходимость применять численные методы, дающие приближенное решение задачи.
Рассмотрим метод Эйлера применительно к уравнению второго порядка. Изложение без особого труда обобщается на случай уравнений более высокого порядка.
Пусть дано уравнение второго порядка
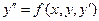 (5)
(5)
с начальными условиями 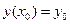 и
и 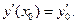 Это уравнение может быть сведено к системе уравнений:
Это уравнение может быть сведено к системе уравнений:

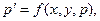 (6)
(6)
с начальными условиями
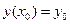 ,
, 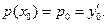 (7)
(7)
При численном решении уравнения (5) задача ставится так:
в точках 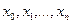 нужно найти приближения
нужно найти приближения 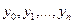 для значений точного решения
для значений точного решения 
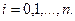 Чаще всего
Чаще всего 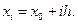 Точки
Точки 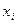 называются узлами сетки, а величины
называются узлами сетки, а величины 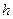 - шагом
- шагом 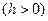 . Во многих случаях удобно величину
. Во многих случаях удобно величину 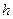 принимать постоянной.
принимать постоянной.
По определению производной имеем
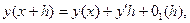
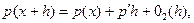 (8)
(8)
где 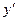 и
и  берутся в точке
берутся в точке  , и величины
, и величины 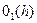 и
и 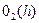 стремятся к нулю при
стремятся к нулю при 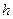 , стремящемся к нулю. Подставляя в (8) вместо
, стремящемся к нулю. Подставляя в (8) вместо  значение
значение 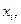
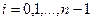 и вместо
и вместо 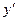 и
и  их выражения из (6), получаем
их выражения из (6), получаем
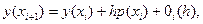 (9)
(9)
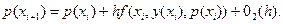
Отсюда видно, что приближенные значения функции 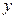 и
и 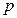 в точке
в точке 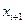
целесообразно вычислять следующим образом:
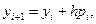
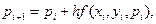 (10)
(10)
Согласно заданному варианту № 2-1, на отрезке [0; 1] составить таблицу значений приближенного решения системы дифференциальных уравнений
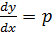 ,
,
 -0.03
-0.03 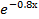 , (11)
, (11)
c начальным условиям 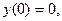
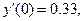 выбрав при этом шаг интегрирования
выбрав при этом шаг интегрирования 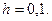
На основе метода Эйлера приближенное решение уравнения (11) можно представить системой уравнений первого порядка в следующем виде:
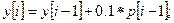

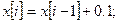
с начальными условиями: 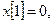

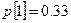 .
.
Программа решения дифференциального уравнения (11) представлена на рисунке 1.
disp('Метод Эйлера');
n=9;
h=0.1;
x(1)=0; y(1)=0; p(1)=0.25;
for i=2: n x(i)=x(i-1)+h;
y(i)=y(i-1)+h*p(i-1);
p(i)=p(i-1)+h*(-0.03*exp(-0.8*x(i-1)));
end
disp('Результаты счета');
for i=1: 9
fprintf('x(i)=%7.4f y(i)=%7.4f p=%7.4f\n'...
, x(i), y(i), p(i));
end
Рисунок 1.
Результаты счета:
x(i)= 0.0000 y(i)= 0.0000 p= 0.2500
x(i)= 0.1000 y(i)= 0.0250 p= 0.2470
x(i)= 0.2000 y(i)= 0.0497 p= 0.2442
x(i)= 0.3000 y(i)= 0.0741 p= 0.2417
x(i)= 0.4000 y(i)= 0.0983 p= 0.2393
x(i)= 0.5000 y(i)= 0.1222 p= 0.2371
x(i)= 0.6000 y(i)= 0.1459 p= 0.2351
x(i)= 0.7000 y(i)= 0.1694 p= 0.2333
x(i)= 0.8000 y(i)= 0.1928 p= 0.2316
Рисунок 2.
Программа алгоритма метода Рунге – Кутта для решения дифференциального уравнения (11) представлена на рисунке 3.
function difur
y0=[0; 0.25] ts=0:.1: 1;
dydt=@(t, y)[y(2); -0.03*exp(-0.8*t)];
[t0, y0]=ode45(dydt, ts, y0)
end
Рисунок 3.
Переходные процессы переменных y(1) и y(2) представлены на рисунке 4.
y0 =0 0.2500 (Начальные условия)
t0 = 0
0.1000
0.2000
0.3000
0.4000
0.5000
0.6000
0.7000
0.8000
0.9000
1.0000
Y(1) y(2)
0.0249 0.2471
0.0494 0.2445
0.0738 0.2420
0.0978 0.2397
0.1217 0.2376
0.1454 0.2357
0.1688 0.2339
0.1922 0.2323
0.2153 0.2308
0.2383 0.2293
Рисунок 4.
|