Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Центральное и параллельное проецирование
|
|
| Aп |
| S |
| A |
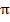1 и центром проекций – точкой S, не лежащей в этой плоскости. Чтобы спроецировать некоторую точку А пространства на плоскость П нужно через центр проецирования S и точку А провести прямую (проецирующий луч) до пересечения ее с плоскостью П в точке Aп. Точку Ап называют центральной проекцией точки А
Метод центрального проецирования достаточно сложен и в
значительной мере искажает форму и размеры оригинала, так как
не сохраняет параллельности прямых и отношения отрезков. По этому на практике чаще пользуются методом параллельного проецирования. Параллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления. Пусть требуется построить параллельную проекцию кривой k на плоскость П 1(рис.1.2). Спроецируем в направлении s все точки кривой k на плоскость П 1. Чтобы спроецировать точки указанной кривой, например А, В, С, нужно провести через них прямые, параллельные направлению s, до пересечения с плоскостью П 1. Точки пересечения A 1, B 1, C 1 проецирующих лучей с плоскостью П 1 и будут параллельными проекциями точек А, В и С. Таким образом можно построить проекции множества точек кривой k. В зависимости от направления проецирования по отношению к плоскости проекций П 1 различают два вида параллельных проекций: косоугольную, когда проецирующие лучи не перпендикулярны к плоскости П 1 (рис. 1.2, кривая k), и прямоугольную (или ортогональную), когда проецирующие лучи перпендикулярны к плоскости проекций (рис.1.2, прямая а). Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции, особенно ортогональные, обладают удобоизмеримостью и простотой построения. Поэтому ортогональное проецирование широко распространено в технике и является основным методом начертательной геометрии.