Краткие теоретические сведения и основные формулы

Литература

Основная: Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высшая школа, 1989. - Гл. 27, § 27.3; гл. 28, § 28.1, 28.3; гл. 30.

Дополнительная: Савельев И.В. Курс общей физики. - М.: Наука, 1987. - Т. 2. - гл. 13, 15.

Контрольные вопросы для подготовки к занятию

1. Дайте определение и начертите колебательный контур.

2. Какой контур называется идеальным контуром Томсона? Поясните возникновение и поддержание электрических колебаний в идеальном контуре.

3. Запишите дифференциальное уравнение свободных незатухающих электромагнитных колебаний в идеальном контуре и его решение в тригонометрическом виде.

4. По каким формулам определяются собственная частота контура и период свободных незатухающих электромагнитных колебаний?

5. Напишите выражение для силы тока в идеальном колебательном контуре и напряжения на конденсаторе.

6. Приведите формулы энергии электрического и магнитного полей для идеального колебательного контура и запишите закон сохранения энергии при наличии свободных гармонических колебаний в нем.

7. Запишите дифференциальное уравнение затухающих колебаний заряда в контуре и его решение в тригонометрической форме.

8. По каким формулам определяются частота затухающих колебаний и период затухания колебаний?

9. Приведите формулы логарифмического декремента затухания и добротности контура. От чего зависит коэффициент затухания?

10. Начертите схему включения переменного напряжения в колебательный контур.

11. Запишите дифференциальное уравнение вынужденных колебаний в колебательном контуре и его решение в тригонометрическом виде. Поясните их.

12. По каким формулам определяются индуктивное, емкостное и полное сопротивления колебательного контура, сдвиг фаз между силой тока и напряжением?

13. Начертите векторную диаграмму для контура, содержащего последовательно соединенные источник питания, активное сопротивление, индуктивность и емкость. Запишите закон Ома для такого контура.

14. При какой частоте возникает явление резонанса? Начертите резонансные кривые напряжения и тока и поясните их.

15. Запишите уравнение плоской электромагнитной волны и поясните физический смысл величин.

Краткие теоретические сведения и основные формулы

Электрические явления, при которых происходит периодическое изменение электрических величин, называются электромагнитными колебаниями.

Колебательный контур – электрическая цепь, состоящая из последовательно соединенных конденсатора электроемкостью С, катушки индуктивности L и резистора R (рис. 24.1). В сопротивление R входит также сопротивление обмотки катушки.

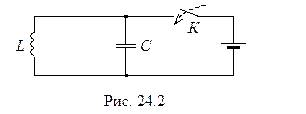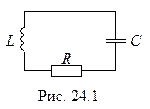В идеальном контуре Томсона (рис. 24.2), в котором сопротивление пренебрежимо мало (R = 0) и потерей энергии на нагревание проводов также можно пренебречь, возникают свободные незатухающие колебания заряда конденсатора и тока в катушке.

Дифференциальное уравнение свободных незатухающих колебаний заряда q в идеальном контуре

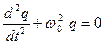. (24.1)

Циклическая частота 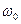и период Т этих колебаний удовлетворяют формуле Томсона

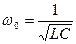; (24.2)

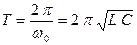. (24.3)

Заряд q конденсатора и сила тока I в контуре изменяются по законам

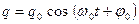; (24.4)

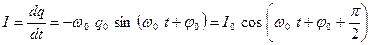, (24.5)

где 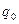- амплитуда заряда конденсатора, 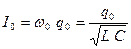- амплитуда силы тока, 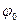- начальная фаза колебаний заряда конденсатора.

Разность потенциалов обкладок конденсатора 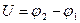также изменяется по гармоническому закону:

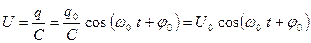. (24.6)

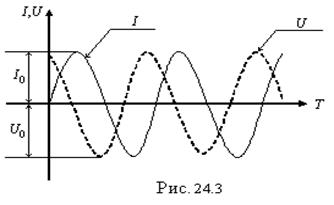
Из выражений (24.6) и (24.5) вытекает, что колебания тока I опережают по фазе колебания заряда q на 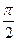(рис. 24.3), т.е. когда ток достигает максимального значения, заряд и совпадающее по фазе с зарядом напряжение обращаются в нуль и наоборот.

Полная энергия колебаний складывается из энергии электрического W_e и магнитного поля .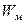

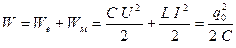. (24.7)

Электрическое сопротивление реального контура R ≠ 0, дифференциальное уравнение свободных затухающих колебаний в этом контуре имеет вид

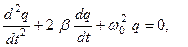(24.8)

где 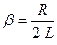- коэффициент затухания и .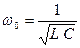